1.线性结构的定义
线性结构是由零个或多个具有相同类型的数据元素组成的的有限序列,如下图所示

在数据元素的非空有限集中
- 存在唯一的一个被称作“第一个”的数据元素
- 存在唯一的一个被称作“最后一个”的数据元素
- 除第一个元素外,集合中的每个数据元素均只有一个前驱
- 除最后一个元素外,集合中的每个数据元素均只有一个后继
简言之,线性结构反映结点间的逻辑关系是 一对一 的。
线性结构包括线性表、栈、队列、字符串、数组等。其中最典型、最常用的是线性表。
在较复杂的线性表中,一个数据元素可以由若干个数据项组成

2.线性表的存储结构
2.1.线性表的顺序存储结构
顺序存储定义:把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构。简言之,逻辑上相邻,物理上也相邻。
顺序存储方法:用一组地址连续的存储单元依次存储线性表的元素,可通过数组V[n]来实现。

线性表的顺序存储结构(顺序表)中的数据元素之间的逻辑关系可以以元素在计算机内“物理位置相邻”来表示。每一个元素的存储位置和线性表的起始位置相差一个和数据元素在线性表中的位序成正比的常数。只要确定了存储线性表的起始位置,线性表中任一数据元素都可随机存取,所以线性表的顺序存储结构是一种随机存取的存储结构。
由于数组类型也有随机存取的特性,因此通常用数组来描述数据结构中的顺序存储结构。
线性表的顺序存储结构的特点
- 逻辑上相邻的数据元素,其物理上也相邻
- 若已知表中首元素在存储器中的位置,则其他元素存放位置亦可求出(利用数组下标)
-
设首元素a1的存放地址为LOC(a1)(称为首地址),设每个元素占用存储空间(地址长度)为L字节,则表中任一数据元素的存放地址为:
LOC(ai) = LOC(a1) + L *(i-1)
LOC(ai+1) = LOC(ai)+L
-
注意:C语言中的数组的下标从0开始,即:V[n]的有效范围是V[0]~V[n-1]
2.1.1.线性表顺序存储结构的定义
由于线性表的长度可变,且所需的最大存储空间随问题的不同而不同,则在C语言中可用动态分配的一维数组来表示。
typedef unsigned int TSeqListNode; typedef struct _tag_SeqList { int capacity;//顺序表的容量 int length; //顺序表当前长度 TSeqListNode* node; //节点存储空间的基址 } TSeqList;
2.1.2.线性表顺序存储结构的初始化
上述定义中,数组指针node指示线性表的基地址,length指示线性表的当前长度。顺序表的初始化操作就是为顺序表分配一个预定义大小的数组空间并将线性表的当前长度设为0。capacity指示顺序表当前分配的存储空间大小,一旦因插入操作而空间不足时,可进行再分配。
/*创建一个预定义大小为capacity的顺序表*/ SeqList* SeqList_Create(int capacity) { //指向创建的顺序表的指针,初始化为NULL TSeqList* ret = NULL; //为线性表申请内存空间,大小为线性表本身的大小+线性表节点大小×线性表的容量 if( capacity >= 0 ) { ret = (TSeqList*)malloc(sizeof(TSeqList) + sizeof(TSeqListNode) * capacity); } //申请内存成功 if( ret != NULL ) { //线性表的容量设置为capacity ret->capacity = capacity; //线性表当前的长度为0 ret->length = 0; //线性表节点存储空间的基址 ret->node = (TSeqListNode*)(ret + 1); } return ret; }
C语言中数组的下标从0开始,因此,若L是SqList类型的顺序表,则表中第i个数据元素是L.elem[i-1]。
2.1.3.线性表顺序存储结构的插入操作
在第i(1<=i <=n)个元素之前插入一个元素时,需将第n至第i(共n-i+1)个元素向后移动一个位置。

int SeqList_Insert(SeqList* list, SeqListNode* node, int pos) { TSeqList* sList = (TSeqList*)list; int ret = (sList != NULL); int i = 0; //插入的位置必须大于等于0,插入后线性表的长度应小于容量 ret = ret && (sList->length + 1 <= sList->capacity); ret = ret && (0 <= pos); if( ret ) { //如果插入的位置大于线性表当前长度,则将元素插入到length位置 if( pos >= sList->length ) { pos = sList->length; } //pos位置后的每一个元素都向后移动一个位置 for(i=sList->length; i>pos; i--) { sList->node[i] = sList->node[i-1]; } //pos位置节点设置为要插入的节点 sList->node[i] = *(TSeqListNode)node; //线性表当前长度+1 sList->length++; } return ret; }
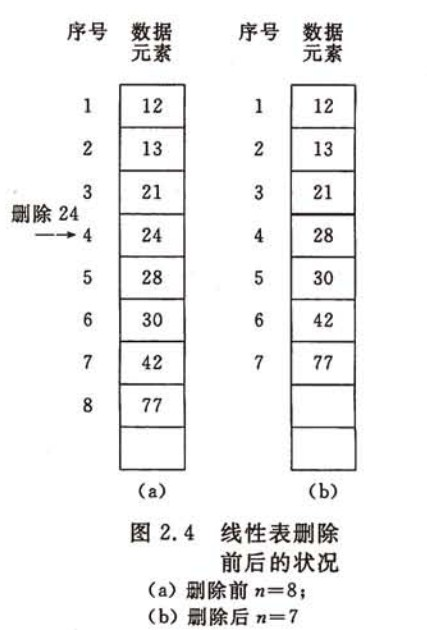
2.1.4.线性表的顺序存储结构的删除操作
删除第i(1<= i <= n)个元素时,需将第i+1至第n(共n-i)个元素依次向前移动一个位置
SeqListNode* SeqList_Delete(SeqList* list, int pos) // O(n) { TSeqList* sList = (TSeqList*)list; //获取要删除的位置的节点作为函数的返回值 SeqListNode* ret = SeqList_Get(list, pos); int i = 0; if( ret != NULL ) { //第i+1之后的元素依次向前移动一个位置 for(i=pos+1; i<sList->length; i++) { sList->node[i-1] = sList->node[i]; } //顺序表当前长度-1 sList->length--; } return ret; }
2.1.5.线性表的顺序存储结构的查找操作
在顺序表L中查找是否存在和e相同的数据元素最简单的方法是,令e和L中的元素逐个比较之
SeqListNode* SeqList_Get(SeqList* list, int pos) { TSeqList* sList = (TSeqList*)list; SeqListNode* ret = NULL; //保证线性表不为空,pos大于等于0并且小于线性表的当前长度 if( (sList != NULL) && (0 <= pos) && (pos < sList->length) ) { //返回当前位置的节点 ret = (SeqListNode*)(&(sList->node[pos])); } return ret; }
2.1.6.线性表的顺序存储结构的代码实现
//SeqList.h #ifndef _SEQLIST_H_ #define _SEQLIST_H_ typedef void SeqList; typedef void SeqListNode; SeqList* SeqList_Create(int capacity); void SeqList_Destroy(SeqList* list); void SeqList_Clear(SeqList* list); int SeqList_Length(SeqList* list); int SeqList_Capacity(SeqList* list); int SeqList_Insert(SeqList* list, SeqListNode* node, int pos); SeqListNode* SeqList_Get(SeqList* list, int pos); SeqListNode* SeqList_Delete(SeqList* list, int pos); #endif
//SeqList.c #include <stdio.h> #include <malloc.h> #include "SeqList.h" typedef unsigned int TSeqListNode; typedef struct _tag_SeqList { int capacity; int length; TSeqListNode* node; } TSeqList; SeqList* SeqList_Create(int capacity) { TSeqList* ret = NULL; if( capacity >= 0 ) { ret = (TSeqList*)malloc(sizeof(TSeqList) + sizeof(TSeqListNode) * capacity); } if( ret != NULL ) { ret->capacity = capacity; ret->length = 0; ret->node = (TSeqListNode*)(ret + 1); } return ret; } void SeqList_Destroy(SeqList* list) { free(list); } void SeqList_Clear(SeqList* list) { TSeqList* sList = (TSeqList*)list; if( sList != NULL ) { sList->length = 0; } } int SeqList_Length(SeqList* list) { TSeqList* sList = (TSeqList*)list; int ret = -1; if( sList != NULL ) { ret = sList->length; } return ret; } int SeqList_Capacity(SeqList* list) { TSeqList* sList = (TSeqList*)list; int ret = -1; if( sList != NULL ) { ret = sList->capacity; } return ret; } int SeqList_Insert(SeqList* list, SeqListNode* node, int pos) { TSeqList* sList = (TSeqList*)list; int ret = (sList != NULL); int i = 0; ret = ret && (sList->length + 1 <= sList->capacity); ret = ret && (0 <= pos); if( ret ) { if( pos >= sList->length ) { pos = sList->length; } for(i=sList->length; i>pos; i--) { sList->node[i] = sList->node[i-1]; } sList->node[i] = *(TSeqListNode*)node; sList->length++; } return ret; } SeqListNode* SeqList_Get(SeqList* list, int pos) { TSeqList* sList = (TSeqList*)list; SeqListNode* ret = NULL; if( (sList != NULL) && (0 <= pos) && (pos < sList->length) ) { ret = (SeqListNode*)(&(sList->node[pos])); } return ret; } SeqListNode* SeqList_Delete(SeqList* list, int pos) { TSeqList* sList = (TSeqList*)list; SeqListNode* ret = SeqList_Get(list, pos); int i = 0; if( ret != NULL ) { for(i=pos+1; i<sList->length; i++) { sList->node[i-1] = sList->node[i]; } sList->length--; } return ret; }
//main.c #include <stdio.h> #include <stdlib.h> #include "SeqList.h" int main(int argc, char *argv[]) { SeqList* list = SeqList_Create(5); int i = 0; int j = 1; int k = 2; int x = 3; int y = 4; int z = 5; int index = 0; SeqList_Insert(list, &i, 0); SeqList_Insert(list, &j, 0); SeqList_Insert(list, &k, 0); SeqList_Insert(list, &x, 0); SeqList_Insert(list, &y, 0); SeqList_Insert(list, &z, 0); for(index=0; index<SeqList_Length(list); index++) { int* p = (int*)SeqList_Get(list, index); printf("%d ", *p); } printf(" "); while( SeqList_Length(list) > 0 ) { int* p = (int*)SeqList_Delete(list, 0); printf("%d ", *p); } SeqList_Destroy(list); return 0; }
2.1.7.线性表的顺序存储结构的优缺点
优点:
- 逻辑相邻,物理相邻
- 可随机存取任一元素
- 存储空间使用紧凑
缺点:
- 插入、删除操作需要移动大量的元素
- 预先分配空间需按最大空间分配,利用不充分
- 表容量难以扩充
- 事实上,链表插入、删除运算的快捷是以空间代价来换取时间
2.2.线性表的链式存储结构
2.2.1.线性表的链式存储的表示
- 链式存储结构特点:其结点在存储器中的位置是随意的,即逻辑上相邻的数据元素在物理上不一定相邻。
- 如何实现?通过指针来实现
-
注意:每个存储结点都包含两部分:数据域和指针域
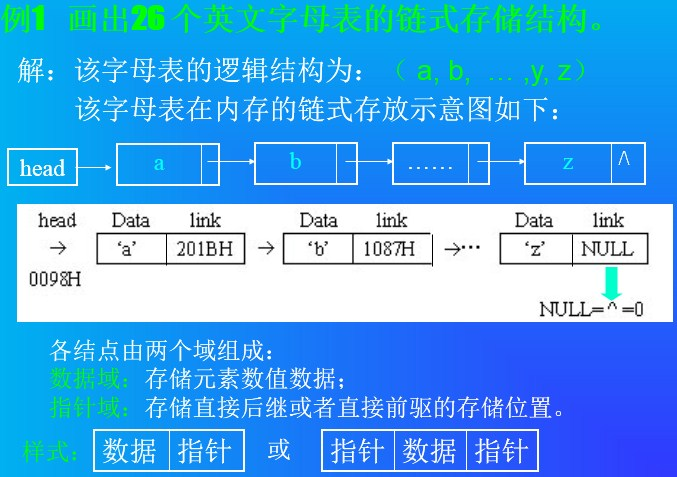
用线性链表表示线性表时,数据元素之间的逻辑关系是由结点中的指针指示的。由上图可见单链表可由头指针唯一确定,在C语言中可用“结构指针”来描述。
2.2.2.线性表的链式存储结构的定义
struct Node; /* 单链表结点类型 */ typedef struct Node *PNode; /* 结点指针类型 */ typedef struct Node *LinkList; /* 单链表类型 */ struct Node { /* 单链表结点结构 */ DataType info; PNode link; };
假设L是LinkList型的变量,则L为单链表的头指针它指向表中第一个结点。若L为空(L=NULL),则所表示的线性表为空表,其长度n为0。有时,我们在单链表的第一个节点之前附设一个结点,称之为头结点,头结点的数据域可以不存储任何信息,也可以存储如线性表长度等类的附加信息。头结点的指针域存储指向第一个结点的指针(即第一个元素结点的存储位置)单链表的头指针指向头结点,若线性表为空表则头结点的指针域为空。

2.2.3.线性表的链式存储结构的初始化
单链表是一种动态结构,整个可用存储空间可为多个链表共同享用每个链表占用的空间不需要预先分配划定,而是可以由系统应需求即时生成。因此建立线性表的链式存储结构的过程就是一个动态生成链表的过程。即从“空表”的初始状态起,依次建立各个元素结点,并逐个插入链表(也可以只生成一个空链表)。
/* 创建一个带头结点的空链表 */ LinkList createNullList_link( void ) { LinkList llist; llist = (LinkList)malloc( sizeof( struct Node ) ); /* 申请表头结点空间 */ if( llist != NULL ) llist->link = NULL; return llist; }
2.2.4.线性表的链式存储结构的插入操作
假如我们要在线性表的两个数据元素a和b之间插入一个数据元素x,已知p为其单链表存储结构中指向结点a的指针。
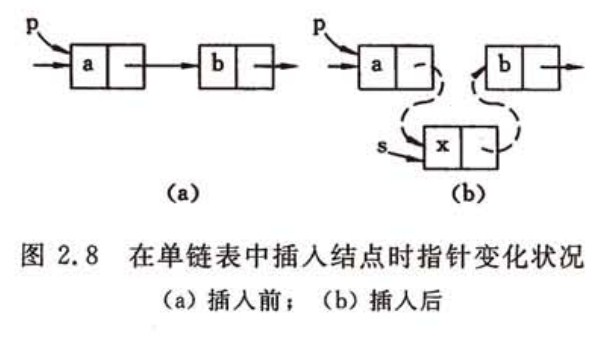
为了插入元素x,首先要生成一个数据域为x的结点,然后插入在单链表中。根据插入操作的逻辑定义,还需要修改结点a中的指针域,令其指向结点x而结点x中的指针域应当指向结点b。假设s为指向结点x的指针,则上述指针修改用语句描述即为
s->next = p->next;
p->next = s;
算法实现
/* 在llist带头结点的单链表中下标为i的(第i+1个)结点前插入元素x */ int insert_link(LinkList llist, int i, DataType x) { PNode p = llist, q; int j; for (j = 0 ; p != NULL && j < i; j++) /* 找下标为i-1的(第i个)结点 */ p = p->link; if (j != i) { /* i<1或者大于表长 */ printf("Index of link-list is out of range. ",i); return 0; } q = (PNode)malloc( sizeof( struct Node ) ); /* 申请新结点 */ if( q == NULL ) { printf( "Out of space! " ); return 0; } /* 插入链表中 */ q->info = x; q->link = p->link; p->link = q; /* 注意该句必须在上句后执行 */ return 1 ; }
2.2.5.线性表的链式存储结构的删除操作

在线性表中删除元素b时,仅需修改结点a中的指针域即可,假设p为指向结点a的指针,则修改指针的语句为
p->next = p->next->next;
算法实现
/* 在llist带有头结点的单链表中删除第一个值为x的结点 */ /* 这时要求 DataType 可以用 != 比较 */ int delete_link( LinkList llist, DataType x ) { PNode p = llist, q; /*找值为x的结点的前驱结点的存储位置 */ while( p->link != NULL && p->link->info != x ) p = p->link; if( p->link == NULL ) { /* 没找到值为x的结点 */ printf("Datum does not exist! "); return 0; } q = p->link; /* 找到值为x的结点 */ p->link = p->link->link; /* 删除该结点 */ free( q ); return 1; }
2.2.6.线性表的链式存储结构的查找操作
在链表中找到第n个节点的方法为,通过循环操作,从头结点开始,不断通过next指针域找到下一个结点的位置。
for(i=0;i<ni++) p = p->next;
通过上面的操作之后,p指针指向的就是我们需要的第n个结点的地址。
/* 在llist带有头结点的单链表中找第一个值为x的结点存储位置 */ /* 找不到时返回空指针 */ PNode locate_link( LinkList llist, DataType x ) { PNode p; if (llist == NULL) return NULL; for ( p = llist->link; p != NULL && p->info != x; ) p = p->link; return p; } /* 在带有头结点的单链表llist中下标为i的(第i+1个)结点的存储位置 */ /* 当表中无下标为i的(第i+1个)元素时,返回值为NULL */ PNode find_link( LinkList llist, int i ) { PNode p; int j; if (i < 0) { /* 检查i的值 */ printf("Index of link-list is out of range. ",i); return NULL; } for ( p = llist->link, j = 0; p != NULL && j < i; j++) p = p->link; if (p == NULL) printf("Index of link-list is out of range. ", i); return p; }
2.2.7.线性表的链式存储结构的代码实现
//LinkList.h #ifndef _LINKLIST_H_ #define _LINKLIST_H_ typedef void LinkList; typedef struct _tag_LinkListNode LinkListNode; struct _tag_LinkListNode { LinkListNode* next; }; LinkList* LinkList_Create(); void LinkList_Destroy(LinkList* list); void LinkList_Clear(LinkList* list); int LinkList_Length(LinkList* list); int LinkList_Insert(LinkList* list, LinkListNode* node, int pos); LinkListNode* LinkList_Get(LinkList* list, int pos); LinkListNode* LinkList_Delete(LinkList* list, int pos); #endif
//LinkList.c #include <stdio.h> #include <malloc.h> #include "LinkList.h" typedef struct _tag_LinkList { LinkListNode header; int length; } TLinkList; LinkList* LinkList_Create() { TLinkList* ret = (TLinkList*)malloc(sizeof(TLinkList)); if( ret != NULL ) { ret->length = 0; ret->header.next = NULL; } return ret; } void LinkList_Destroy(LinkList* list) { free(list); } void LinkList_Clear(LinkList* list) { TLinkList* sList = (TLinkList*)list; if( sList != NULL ) { sList->length = 0; sList->header.next = NULL; } } int LinkList_Length(LinkList* list) { TLinkList* sList = (TLinkList*)list; int ret = -1; if( sList != NULL ) { ret = sList->length; } return ret; } int LinkList_Insert(LinkList* list, LinkListNode* node, int pos) { TLinkList* sList = (TLinkList*)list; int ret = (sList != NULL) && (pos >= 0) && (node != NULL); int i = 0; if( ret ) { LinkListNode* current = (LinkListNode*)sList; for(i=0; (i<pos) && (current->next != NULL); i++) { current = current->next; } node->next = current->next; current->next = node; sList->length++; } return ret; } LinkListNode* LinkList_Get(LinkList* list, int pos) { TLinkList* sList = (TLinkList*)list; LinkListNode* ret = NULL; int i = 0; if( (sList != NULL) && (0 <= pos) && (pos < sList->length) ) { LinkListNode* current = (LinkListNode*)sList; for(i=0; i<pos; i++) { current = current->next; } ret = current->next; } return ret; } LinkListNode* LinkList_Delete(LinkList* list, int pos) { TLinkList* sList = (TLinkList*)list; LinkListNode* ret = NULL; int i = 0; if( (sList != NULL) && (0 <= pos) && (pos < sList->length) ) { LinkListNode* current = (LinkListNode*)sList; for(i=0; i<pos; i++) { current = current->next; } ret = current->next; current->next = ret->next; sList->length--; } return ret; }
//main.c #include <stdio.h> #include <stdlib.h> #include "LinkList.h" struct Value { LinkListNode header; int v; }; int main(int argc, char *argv[]) { int i = 0; LinkList* list = LinkList_Create(); struct Value v1; struct Value v2; struct Value v3; struct Value v4; struct Value v5; v1.v = 1; v2.v = 2; v3.v = 3; v4.v = 4; v5.v = 5; LinkList_Insert(list, (LinkListNode*)&v1, LinkList_Length(list)); LinkList_Insert(list, (LinkListNode*)&v2, LinkList_Length(list)); LinkList_Insert(list, (LinkListNode*)&v3, LinkList_Length(list)); LinkList_Insert(list, (LinkListNode*)&v4, LinkList_Length(list)); LinkList_Insert(list, (LinkListNode*)&v5, LinkList_Length(list)); for(i=0; i<LinkList_Length(list); i++) { struct Value* pv = (struct Value*)LinkList_Get(list, i); printf("%d ", pv->v); } while( LinkList_Length(list) > 0 ) { struct Value* pv = (struct Value*)LinkList_Delete(list, 0); printf("%d ", pv->v); } LinkList_Destroy(list); return 0; }
2.3.线性表的索引存储结构
有时候也可以使用一维数组来描述链表,只要定义一个结构类型(含数据域和指示域)数组,就可以完全描述链表,这种链表称为静态链表。数据域含义与前面相同,指示域相当于前面的指针域。静态链表的插入与删除操作与普通链表一样,不需要移动元素,只需修改指示器就可以了。

这种描述的方法便于在不设“指针”类型的高级程序设计语言中使用链表结构。在如上描述的链表中,数组的一个分量表示一个结点,同时用游标(指示器cur)代替指针指示结点在数组中的相对位置。数组的第0个分量可以看做头结点,其指针域指示链表的第一个结点。
2.3.1.线性表的索引存储结构的代码实现
//StaticList.h #ifndef _STATICLIST_H_ #define _STATICLIST_H_ typedef void StaticList; typedef void StaticListNode; StaticList* StaticList_Create(int capacity); void StaticList_Destroy(StaticList* list); void StaticList_Clear(StaticList* list); int StaticList_Length(StaticList* list); int StaticList_Capacity(StaticList* list); int StaticList_Insert(StaticList* list, StaticListNode* node, int pos); StaticListNode* StaticList_Get(StaticList* list, int pos); StaticListNode* StaticList_Delete(StaticList* list, int pos); #endif
//StaticList.c #include <stdio.h> #include <malloc.h> #include "StaticList.h" #define AVAILABLE -1 typedef struct _tag_StaticListNode { unsigned int data; int next; } TStaticListNode; typedef struct _tag_StaticList { int capacity; TStaticListNode header; TStaticListNode node[]; } TStaticList; StaticList* StaticList_Create(int capacity) { TStaticList* ret = NULL; int i = 0; if( capacity >= 0 ) { ret = (TStaticList*)malloc(sizeof(TStaticList) + sizeof(TStaticListNode) * (capacity + 1)); } if( ret != NULL ) { ret->capacity = capacity; ret->header.data = 0; ret->header.next = 0; for(i=1; i<=capacity; i++) { ret->node[i].next = AVAILABLE; } } return ret; } void StaticList_Destroy(StaticList* list) { free(list); } void StaticList_Clear(StaticList* list) { TStaticList* sList = (TStaticList*)list; int i = 0; if( sList != NULL ) { sList->header.data = 0; sList->header.next = 0; for(i=1; i<=sList->capacity; i++) { sList->node[i].next = AVAILABLE; } } } int StaticList_Length(StaticList* list) { TStaticList* sList = (TStaticList*)list; int ret = -1; if( sList != NULL ) { ret = sList->header.data; } return ret; } int StaticList_Capacity(StaticList* list) { TStaticList* sList = (TStaticList*)list; int ret = -1; if( sList != NULL ) { ret = sList->capacity; } return ret; } int StaticList_Insert(StaticList* list, StaticListNode* node, int pos) { TStaticList* sList = (TStaticList*)list; int ret = (sList != NULL); int current = 0; int index = 0; int i = 0; ret = ret && (sList->header.data + 1 <= sList->capacity); ret = ret && (pos >=0) && (node != NULL); if( ret ) { for(i=1; i<=sList->capacity; i++) { if( sList->node[i].next == AVAILABLE ) { index = i; break; } } sList->node[index].data = *(unsigned int*) node; sList->node[0] = sList->header; for(i=0; (i<pos) && (sList->node[current].next != 0); i++) { current = sList->node[current].next; } sList->node[index].next = sList->node[current].next; sList->node[current].next = index; sList->node[0].data++; sList->header = sList->node[0]; } return ret; } StaticListNode* StaticList_Get(StaticList* list, int pos) { TStaticList* sList = (TStaticList*)list; StaticListNode* ret = NULL; int current = 0; int object = 0; int i = 0; if( (sList != NULL) && (0 <= pos) && (pos < sList->header.data) ) { sList->node[0] = sList->header; for(i=0; i<pos; i++) { current = sList->node[current].next; } object = sList->node[current].next; ret = (StaticListNode*) (&(sList->node[object].data)); } return ret; } StaticListNode* StaticList_Delete(StaticList* list, int pos) { TStaticList* sList = (TStaticList*)list; StaticListNode* ret = NULL; int current = 0; int object = 0; int i = 0; if( (sList != NULL) && (0 <= pos) && (pos < sList->header.data) ) { sList->node[0] = sList->header; for(i=0; i<pos; i++) { current = sList->node[current].next; } object = sList->node[current].next; sList->node[current].next = sList->node[object].next; sList->node[0].data--; sList->header = sList->node[0]; sList->node[object].next = AVAILABLE; ret = (StaticListNode*)(&(sList->node[object].data)); } return ret; }
//main.c #include <stdio.h> #include <stdlib.h> #include "StaticList.h" int main(int argc, char *argv[]) { StaticList* list = StaticList_Create(10); int index = 0; int i = 0; int j = 1; int k = 2; int x = 3; int y = 4; int z = 5; StaticList_Insert(list, &i, 0); StaticList_Insert(list, &j, 0); StaticList_Insert(list, &k, 0); for(index=0; index<StaticList_Length(list); index++) { int* p = (int*)StaticList_Get(list, index); printf("%d ", *p); } printf(" "); while( StaticList_Length(list) > 0 ) { int* p = (int*)StaticList_Delete(list, 0); printf("%d ", *p); } printf(" "); StaticList_Insert(list, &x, 0); StaticList_Insert(list, &y, 0); StaticList_Insert(list, &z, 0); printf("Capacity: %d Length: %d ", StaticList_Capacity(list), StaticList_Length(list)); for(index=0; index<StaticList_Length(list); index++) { int* p = (int*)StaticList_Get(list, index); printf("%d ", *p); } StaticList_Destroy(list); return 0; }