转载请注明原文链接，谢谢啦！
0. 前言
凡谈机器学习，开山之作必是线性模型。何故？线性是数学表征中最为简单的一种，从而线性模型简单、高效，除了用于初步探索数据分布之外，更是建立机器学习模型中的首选，因为越是简单的模型，泛化性越高，大道至简，所言不虚。本文从数学原理到代码实现，希望能够尽可能的深扒线性模型。
1. 背景引入
机器学习模型中有用于回归的，有用于分类的，二者区别：回归预测的指标值为连续值，分类预测的类别值为离散值。可以用如下例子做一个形象解释：
回归问题：根据父母双方的身高,预测孩子的身高(预测值Υ为连续值)
| 样本编号 | 父亲身高(cm)(Χ1) | 母亲身高(cm)(Χ2) | 孩子身高(cm)(Υ) |
| 0 | 175.4 | 163.2 | 174.7 |
| 1 | 168.2 | 170.8 | 182.8 |
| 2 | 170.5 | 155.6 | 168.3 |
分类问题：根据适龄男青年的条件(“是/有”用“1”表示，“否/无”用“0”表示)，预测有无女朋友(预测值Υ为离散值)
| 样本编号 | 身高(cm)(Χ1) | 颜值(满分10分)(Χ2) | 财富(万RMB)(Χ3) | 是否从事IT行业(Χ4) | 有无女朋友(Υ) |
| 0 | 174.5 | 8 | 40 | 1 | 0 |
| 1 | 162.5 | 4 | 4000 | 0 | 1 |
| 2 | 188.3 | 7 | 30 | 0 | 0 |
| 3 | 176.8 | 6 | 80 | 1 | 1 |
按照上述表格，每一行是一个样本，每一列是一维特征。线性模型既可以用于回归问题，又可以用于分类问题，其本质是找到与特征x1，x2等对应的权重参数Θ1，Θ2等，之后进行线性组合，即建立如下数学表达式(其中Θ0为偏置项)，从而预测y值。权重参数表征每个特征在预测中的重要性。
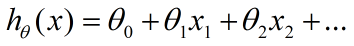
2. 概述
给定样本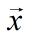
，我们用列向量表示该样本
。
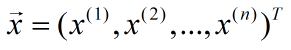样本有n种特征，我们用x(i)表示样本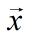的第i个特征。线性模型的形式为：
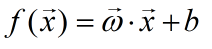
其中：
称为权重向量，其中每个分量是每个特征对应的权重，直观地表达了各个特征在预测中的重要性。
“线性”本质是一系列一次特征的线性组合，在二维空间中是一条直线，在三维空间中是一个平面，推广至n维空间，可以理解为广义线性模型，常见的包括岭回归、lasso回归、Elastic Net、逻辑回归、线性判别分析等。
3. 原理
3.1 普通线性回归
给定数据集
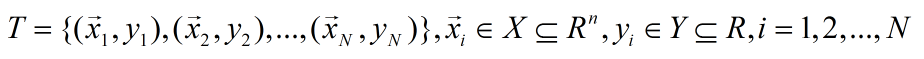
其中：
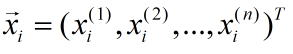
我们需要学习的模型为：
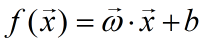
( 模型具体计算过程说明：参数向量的转置与某个样本列向量相乘，或者用样本列项量的转置与参数向量相乘，之后在加上偏置b，得到预测值)
即：根据已知的数据集T来计算参数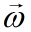 
和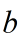
。
在很多讲解机器学习的教程中，这一步就直接给出用平方损失函数作为模型优化目标，如下所示：
给定样本：
其预测值为：
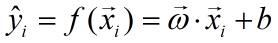
在训练集T上，模型的损失函数为：
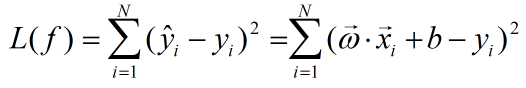
我们的目标是损失函数最小化，即：
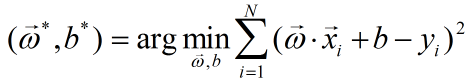
然后就使用梯度下降法求解上述最优化问题的数值解。(有关梯度下降法，参见第4节)
我们在这里就要深扒一下，为什么使用平方损失函数，在数学基础上找到使用平方损失函数的依据。
对于每个样本有如下误差分析：
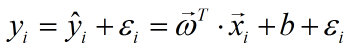
参数向量的转置在上文“ 模型具体计算过程说明”中已介绍；此外，我们为了方便计算，我们可以把偏置当作一个特殊权重，且每一个样本在这一维上的特征值都为1，故上式可以简化为：
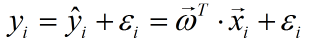
其中，在概率统计学中，绝大多数的误差可以看作是独立并且具有相同分布，并且服从均值为0，方差σ2的高斯分布，则有：
从而可以得到：
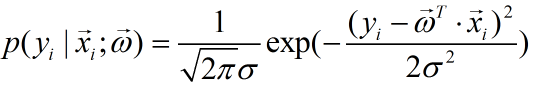
这样，我们对于样本集中的所有样本，就可以得到似然函数，即：
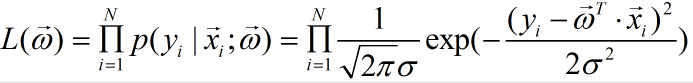
似然可以解释为：我们取什么样的参数与样本进行组合之后，得到的恰好是真实值。而上式就是这种情况在样本集上的概率函数。因为假设每个样本之间是不相关的，即独立同分布，所以我们需要把每个样本此情况下的概率函数累乘。
根据我们的模型预期，我们当然希望这种情况的概率越大越好。也就是说，能使出现这种情况的概率最大的参数向量，就是我们所要求得的参数估计值。这在数学上叫作“最大似然估计”。在概率学中，似然本质上是条件概率。(这里需要理解透彻，后续章节会讲到GMM(混合高斯模型)中，涉及到参数先验、后验、以及似然之间的关系，会进一步详细解释。)
因为计算机系统处理加法要比处理乘法容易得多，所以我们很有必要将似然通过对数乘法法则，转换为对数似然，即有：
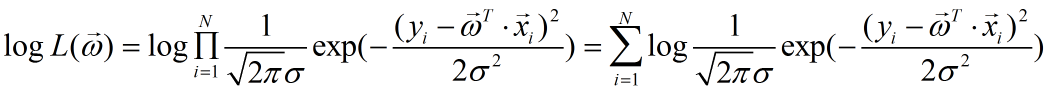
我们对上式的对数似然进行化简，可以得到：
我们预期目标是似然函数越大越好，即对数似然也越大越好，因为对于一个模型来说，样本数、误差的标准差、圆周率都是常数，则对于上式的因子：
应该越小越好。
可以看到，在这里，我们在数学中找到了“用平方损失函数作为模型优化目标”依据，其数学本质上是参数估计方法中的“最大似然估计”。
如果对于一个机器学习模型，我们知道了参数优化目标，似乎我们就可以利用梯度下降方法求解参数估计值了，但是我们在这里还是再深扒一步，因为对于线性模型的优化目标来说，较为简单，在数学中是可以直接用最小二乘法求解解析解，该问题称为多元线性回归。
我们的目标是损失函数最小化，即：
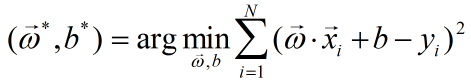
令：
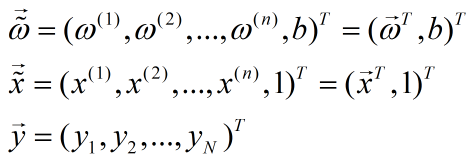
则有：
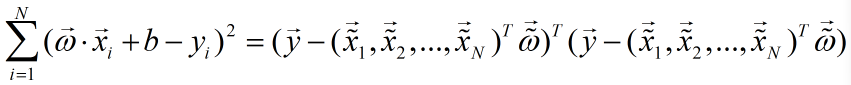
令：
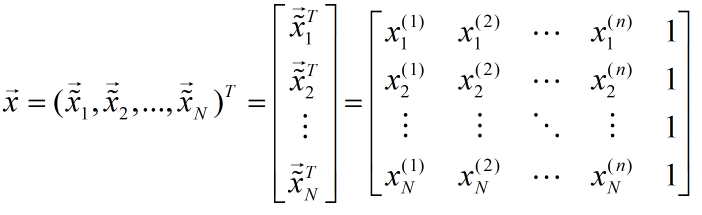
则：
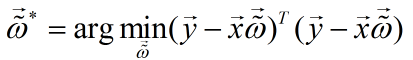
令：
求它的极小值(PS：其中涉及到机器学习领域中有关矩阵运算和求导法则，随后会上传一份资源，以便大家学习使用)，对
求导，并令导数为零，得到解析解：
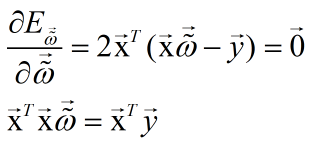
a. 当
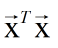
为满秩矩阵或者正定矩阵时，可得：
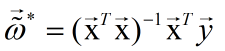
于是学到的多元线性回归模型为：
b. 当
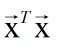
不是满秩矩阵时：比如N<n(样本数量小于特征种类的数量)，根据
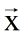
的秩小于等于(N，n)中的最小值，即小于等于N(矩阵的秩一定小于等于矩阵的行数和列数)；因为两矩阵相乘得到的矩阵，它的秩是小于等于两个因子矩阵的秩的最小值(即，若C=AB，则R(C)<=min(R(A)，R(B)。)
而矩阵
是n*n大小的，它的秩一定小于等于N，因此它不是满秩矩阵。此时存在多个解析解。常见的做法是引入L1或L2正则项。以L2正则化为例：
其中λ>0调整正则化项与均方误差的比例；||...||2为L2范数。
根据上述原理，我们得到多元线性回归算法：
输入：
数据集T，正则化项系数λ>0
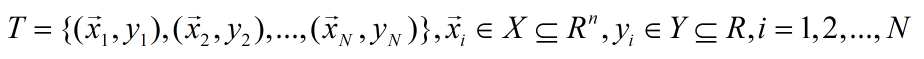
输出：
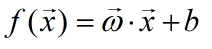
算法步骤：
a. 令：
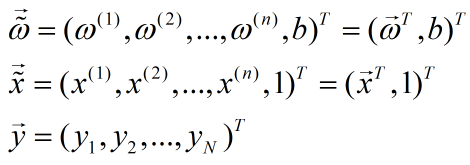
计算：
b. 求解：
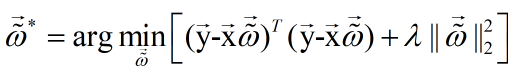
c. 最终学得模型：
3.2 广义线性模型
考虑单调可导函数h(•)，令：
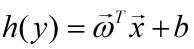
这样得到的模型称为广义线性模型。一个典型的例子就是对数线性回归，即当h(•)=ln(•)时的广义线性模型就是对数线性回归，即：
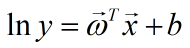
它是通过
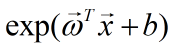
拟合y的。它虽然称为广义线性回归，但实质上是非线性的。
3.3 逻辑回归
上述均是用线性模型进行回归学习，而线性模型也可用于分类，逻辑回归就是利用线性模型进行分类的一种算法。
给定数据集T：
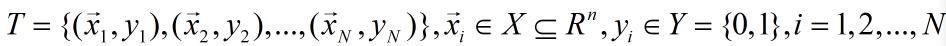
其中：
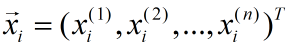
我们需要知道
该条件概率是：在已知测试样本的特征向量后，预测其为相应类的条件概率值。
考虑到
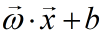
取值是连续的，因此它不能拟合离散变量。但是可以考虑用它来拟合条件概率
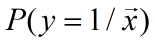
因为概率的取值也是连续的。要拟合概率，其取值范围为0~1，考虑采用广义线性模型，寻找到一个单调可导函数：对数概率函数(logistic function):
由于
则有：
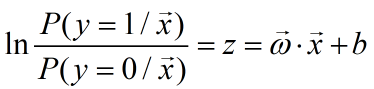
比值
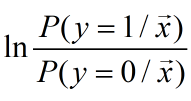
表示样本为正例的可能性比反例的可能性，称为概率(odds)，反映了样本作为正例的相对可能性。概率的对数称为对数概率(log odds，也称为logit)。
逻辑回归模型参数估计，估计原理是极大似然估计法估计模型参数：
将参数b吸收，令：
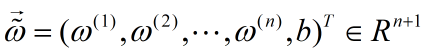
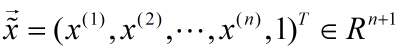
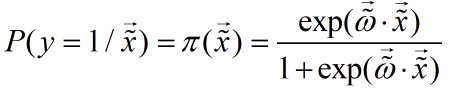
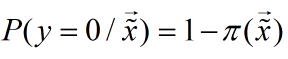
则似然函数为：
对数似然函数为：
又由于
因此：
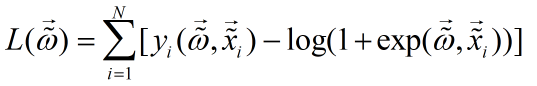
对
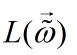
求极大值，
得到
的估计值
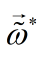
则逻辑回归模型为：
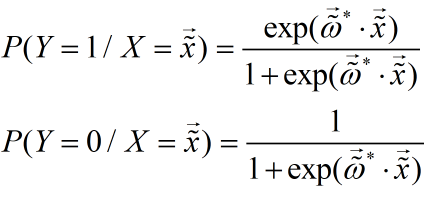
通常用梯度下降法或者拟牛顿法(后续章节会讲到)来求解该最大值问题。
以上讨论都是二类分类的逻辑回归模型，可将此推广到多类分类逻辑回归模型。设离散型随机变量 Y 的取值集合为：{1，2，...，K}，则多分类逻辑回归模型为：
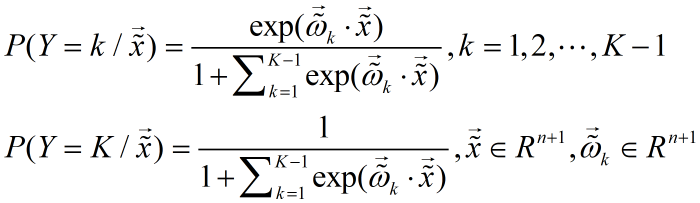
其参数估计方法类似二类分类逻辑回归模型。
3.4 线性判别分析
似二类分
4. 梯度下降
4.1
5. 代码实现
6. sklearn代码实现
7. 补充