20180613小测

这题真是OI题？

T1: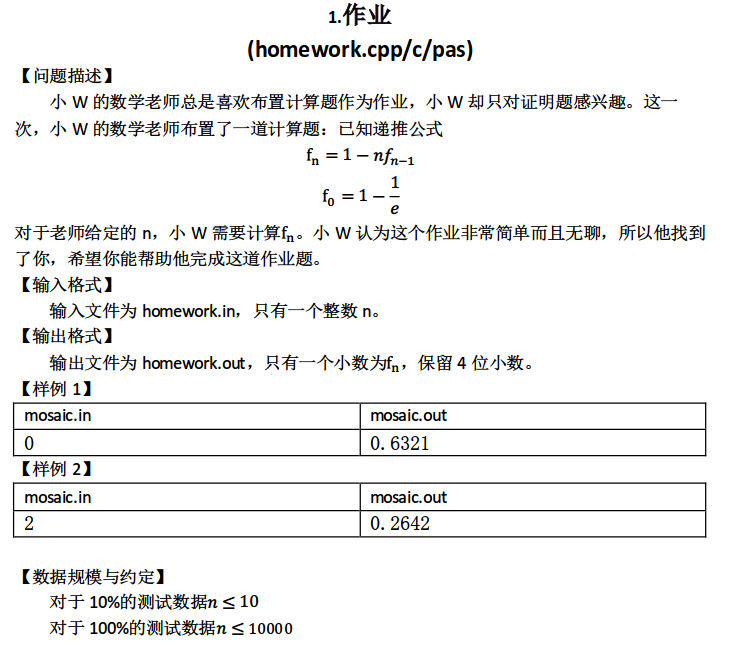

就是给你一个不明觉厉的递推式然后计算东西啦。
首先我们能用long double写一个暴力，发现前几项越来越小，后几项越来越大，明显不对......
考虑为什么，因为计算机中的浮点数是有误差的，这样推的话，误差会被放大到n!级，直接GG！
应该怎样做？手玩了半天发现没什么通项公式，难道写一个带压位FFT能做除法的高精度小数类？然后再求一个3w位有效数字的e？人干事，弃坑弃坑......
于是写了10分暴力。由于没有删调试语句爆了零。
考虑正解怎么做(抄题解？):
首先我们有一个结论:

于是我们可以这样从后向前递推f(n)，不存在精度误差。

(SDFZ某神仙：我观察到这东西绝对值越来越小，于是可以令f(1e5)=0，然后逆推f(n)，于是就这样AC了此题)
如何证明这个结论？
首先我们先构造一个积分:

考虑如何计算？首先我们有: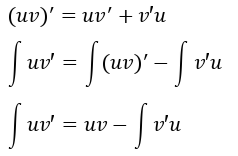

我们令u,v等于如下值，则有: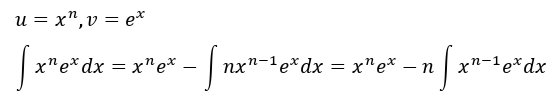

我们钦定g,h为如下意义: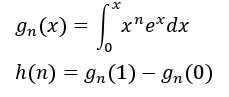

则有:

没错，这东西就是f了。
此外我们有: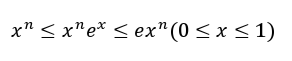

两边同时求积分，可得: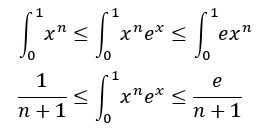

也就是: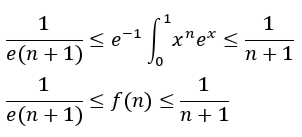

于是我们就证明完了......
(话说这真不是数竞巨佬的来强行出题了？)
考场爆零代码:

#include<cstdio>
#include<cmath>
typedef long double ldb;
const int maxn=1e4+1e2;
const ldb e = exp(1);

ldb f[maxn];

int main() {
    static int n;
    scanf("%d",&n) , *f = 1 - 1 / e;
    for(int i=1;i<=n;i++) f[i] = 1 - i * f[i-1];
    printf("%0.4Lf
",120/e-44);
    printf("%0.4Lf
",f[n]);
    return 0;
}

正解代码:

#include<cstdio>
#include<cmath>
typedef long double ldb;
using namespace std;
const int maxn=1e5+1e2,lim=1e5;
const ldb e = exp(1);

ldb f[maxn];

inline void work() {
    f[lim] = ( 1 / ( lim + 1 ) + 1 / ( ( lim + 1 ) * e ) ) / 2.0;
    for(int i=lim;i;i--) f[i-1] = ( 1 - f[i] ) / i;
}

int main() {
    static int n;
    scanf("%d",&n) , work() , printf("%0.4Lf
",f[n]);
    return 0;
}

T2:

这题什么鬼......
首先不共线的三点确定一个平面，那么我们能找不共线的三个点，钦定第一个点坐标为(0,0)，第二个点在x轴上，第三个点纵坐标非负，这样就确定平面了。
然后轻松地解方程求出其他所有点的坐标，因为题目保证有解，不会存在冲突的。
但是细节很多啊......
首先对于重合的点，我们要先用一个并查集把它们缩起来，否则如果第一个点和第二个点重合了，这题GG。
此外第二个和第三个点坐标的计算方法是要单独写的......
另外，如果前三个基准点共线的话，我们需要直接重选第三个基准点(显然不用重新计算共线那个点的坐标，因为它的位置是确定的)。
然后就可以AC啦！
代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define debug cerr
typedef long double ldb;
using namespace std;
const int maxn=1e2+1e1;
const ldb eps = 1e-4;

inline ldb sq(const ldb &x) {
    return x * x;
}
ldb in[maxn][maxn],x[maxn],y[maxn];
int n,sec,thr;

inline void calc_second() {
    x[sec] = in[1][sec];
}
inline void calc_third() {
    const ldb r1 = in[1][thr] , r2 = in[sec][thr] , rt = in[1][sec];
    const ldb rit = sq(r2) - sq(r1) - sq(rt);
    x[thr] = rit / ( -2 * x[sec] ) , y[thr] = sqrt( sq(r1) - sq(x[thr]) );
}
inline void calc_kth(int k) {
    const ldb r1 = in[1][k] , r2 = in[sec][k] , r3 = in[thr][k];
    const ldb rit = sq(r2) - sq(r1) - sq(in[1][sec]);
    x[k] = rit / ( -2 * x[sec] );
    const ldb rit2 = sq(r3) - sq(r1) - sq(in[1][thr]) + 2 * x[thr] * x[k];
    y[k] = rit2 / ( -2 * y[thr] );
}
inline bool same_line() {
    const ldb dx2 = x[sec] - x[1] , dy2 = y[sec] - y[1];
    const ldb dx3 = x[thr] - x[1] , dy3 = y[thr] - y[1];
    if( fabs( dx2 * dy3 - dx3 * dy2 ) <= eps ) return 1;
    return 0;
}

struct UnionFindSet {
    int fa[maxn];
    inline int findfa(int x) {
        return fa[x] == x ? x : fa[x] = findfa(fa[x]);
    }
    inline void merge(int x,int y) {
        if( findfa(x) != findfa(y) ) fa[findfa(y)] = findfa(x);
    }
    inline void init() {
        for(int i=1;i<=n;i++) fa[i] = i;
    }
}ufs;

inline ldb dis(int i,int j) {
    return sqrt(sq(x[ufs.findfa(i)]-x[ufs.findfa(j)])+sq(y[ufs.findfa(i)]-y[ufs.findfa(j)]));
}

int main() {
    scanf("%d",&n) , ufs.init();
    for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) {
        scanf("%Lf",in[i]+j);
        if( i < j && fabs(in[i][j]) <= eps ) ufs.merge(i,j);
    }
    for(int i=2;i<=n;i++) if( ufs.findfa(i) == i ) {
        if( !sec ) sec = i;
        else if( !thr ) {thr = i; break;}
    }
    if( sec ) calc_second();
    if( thr ) calc_third();
    for(int i=thr+1;i<=n;i++) if( ufs.findfa(i) == i ) {
        if( same_line() ) thr = i , calc_third();
        else calc_kth(i);
    }
    for(int i=1;i<=n;i++) printf("%Lf %Lf
",x[ufs.findfa(i)],y[ufs.findfa(i)]);
    return 0;
}

T3:

题目描述就是给你一个矩阵的第一行，让你构造一个值域满足要求的矩阵使其行列式为1。
由于矩阵转置行列式不变，我们可以先把第一行转置为第一列，最后再转置回来。
由于题目保证存在两个数gcd为1，那么我们可以枚举是哪两个数的gcd为1，用辗转相除消元把矩阵的第一列消成仅有一个1。
然后再枚举对角线上的值是+1还是-1，把消元的过程逆回去，看值域是否满足要求。
为什么要两遍枚举？为了保证不把有解的情况由于值域问题判定为无解。
于是这样写就能获得90分啦！
(为什么少10分？因为我有一个地方的swap没有应用上。话说这样才只扣10分)
考场90分代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#define debug cout
typedef long long int lli;
using namespace std;
const int maxn=7,lim=2e3;

inline lli gcd(lli x,lli y) {
    if( !x || !y ) return x | y;
    register lli t;
    while( ( t = x % y ) ) x = y , y = t;
    return y;
}

lli in[maxn],way[maxn],ans[maxn][maxn];
lli ope[maxn*maxn*maxn],sou[maxn*maxn*maxn],tar[maxn*maxn*maxn],mul[maxn*maxn*maxn];
int n,fs,cnt,lastnum;

inline bool judge() {
    for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if( abs(ans[i][j]) > lim ) return 0;
    return 1;
}
inline bool solve_sta(int ss) {
    memset(ans,0,sizeof(ans));
    int pi = 1; ans[1][1] = 1;
    for(int i=2;i<=n;i++) {
        if( ss & ( 1 << ( i - 2 ) ) ) ans[i][i] = -1;
        else ans[i][i] = 1;
        pi *= ans[i][i];
    }
    if( pi != lastnum ) return 0;
    for(int i=cnt;i;i--) {
        if( ope[i] == 1 ) { // swap
            for(int j=1;j<=n;j++) swap(ans[sou[i]][j],ans[tar[i]][j]);
        } else {
            for(int j=1;j<=n;j++) ans[tar[i]][j] += ans[sou[i]][j] * mul[i];
        }
    }
    return judge();
}
inline bool getway() {
    static int lasti=1,lastj=0;
    cnt = 0 , lastnum = 1;
    for(int i=1;i<=n;i++) way[i] = in[i];
    for(;lasti<=n;lasti++,lastj=0) {
        for(lastj++;lastj<=n;lastj++) if( lasti != lastj && gcd(in[lasti],in[lastj]) == 1 ) {
            while( way[lasti] && way[lastj] ) {
                if( way[lasti] > way[lastj] ) ope[++cnt] = 1 , sou[cnt] = lasti , tar[cnt] = lastj , lastnum *= -1 , swap(way[lasti],way[lastj]);
                int t = way[lastj] / way[lasti];
                ope[++cnt] = 0 , sou[cnt] = lasti , tar[cnt] = lastj , mul[cnt] = t , way[lastj] %= way[lasti];
            }
            if( !way[lasti] ) ope[++cnt] = 1 , sou[cnt] = lasti , tar[cnt] = lastj , lastnum *= -1 , swap(way[lasti],way[lastj]);
            if( lasti != 1 ) ope[++cnt] = 1 , sou[cnt] = lasti , tar[cnt] = 1 , lastnum *= 1;
            for(int j=2;j<=n;j++) if( way[j] ) ope[++cnt] = 0 , sou[cnt] = 1 , tar[cnt] = j , mul[cnt] = way[j] , way[j] = 0;
            return 1;
        }
    }
    return 0;
}

int main() {
    scanf("%d",&n) , fs = 1 << ( n - 1 );
    for(int i=1;i<=n;i++) scanf("%lld",in+i);
    for(int i=1;i<=n;i++) debug<<in[i]<<" "; debug<<endl;
    while(getway()) for(int ss=0;ss<fs;ss++) if( solve_sta(ss) ) {
        for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) printf("%lld%c",ans[j][i],j!=n?' ':'
');
        return 0;
    }
    puts("no solution");
    return 0;
}

正解代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#define debug cout
typedef long long int lli;
using namespace std;
const int maxn=7,lim=2e3;

inline lli gcd(lli x,lli y) {
    if( !x || !y ) return x | y;
    register lli t;
    while( ( t = x % y ) ) x = y , y = t;
    return y;
}

lli in[maxn],way[maxn],ans[maxn][maxn];
lli ope[maxn*maxn*maxn],sou[maxn*maxn*maxn],tar[maxn*maxn*maxn],mul[maxn*maxn*maxn];
int n,fs,cnt,lastnum;

inline bool judge() {
    for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if( abs(ans[i][j]) > lim ) return 0;
    return 1;
}
inline bool solve_sta(int ss) {
    memset(ans,0,sizeof(ans));
    int pi = 1; ans[1][1] = 1;
    for(int i=2;i<=n;i++) {
        if( ss & ( 1 << ( i - 2 ) ) ) ans[i][i] = -1;
        else ans[i][i] = 1;
        pi *= ans[i][i];
    }
    if( pi != lastnum ) return 0;
    for(int i=cnt;i;i--) {
        if( ope[i] == 1 ) { // swap
            for(int j=1;j<=n;j++) swap(ans[sou[i]][j],ans[tar[i]][j]);
        } else {
            for(int j=1;j<=n;j++) ans[tar[i]][j] += ans[sou[i]][j] * mul[i];
        }
    }
    return judge();
}
inline bool getway() {
    static int lasti=1,lastj=0;
    cnt = 0 , lastnum = 1;
    for(int i=1;i<=n;i++) way[i] = in[i];
    for(;lasti<=n;lasti++,lastj=0) {
        for(lastj++;lastj<=n;lastj++) if( lasti != lastj && gcd(in[lasti],in[lastj]) == 1 ) {
            while( way[lasti] && way[lastj] ) {
                if( way[lasti] > way[lastj] ) ope[++cnt] = 1 , sou[cnt] = lasti , tar[cnt] = lastj , lastnum *= -1 , swap(way[lasti],way[lastj]);
                int t = way[lastj] / way[lasti];
                ope[++cnt] = 0 , sou[cnt] = lasti , tar[cnt] = lastj , mul[cnt] = t , way[lastj] %= way[lasti];
            }
            if( !way[lasti] ) ope[++cnt] = 1 , sou[cnt] = lasti , tar[cnt] = lastj , lastnum *= -1 , swap(way[lasti],way[lastj]);
            if( lasti != 1 ) ope[++cnt] = 1 , sou[cnt] = lasti , tar[cnt] = 1 , lastnum *= -1 , swap(way[lasti],way[1]);
            for(int j=2;j<=n;j++) if( way[j] ) ope[++cnt] = 0 , sou[cnt] = 1 , tar[cnt] = j , mul[cnt] = way[j] , way[j] = 0;
            return 1;
        }
    }
    return 0;
}

int main() {
    scanf("%d",&n) , fs = 1 << ( n - 1 );
    for(int i=1;i<=n;i++) scanf("%lld",in+i);
    while(getway()) for(int ss=0;ss<fs;ss++) if( solve_sta(ss) ) {
        for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) printf("%lld%c",ans[j][i],j!=n?' ':'
');
        return 0;
    }
    puts("no solution");
    return 0;
}

这次只是在本学校Rank1了，SDFZ的那个神仙比我高10分......(话说我怎么会犯一些这么蠢的错误呢)

「你说，那片云的背后，又会是什么呢？」
「大概是一望无际的晴空吧。」
「但是，这和我，又有什么关系呢？」
只是这样想着，悲伤便满溢出来。

(不是，为什么要加这段话？)