一、内部排序:是一个逐步扩大记录有序序列长度的过程
其中,希尔排序不稳定
1.直接插入排序:O(n*n)、O(1)
基于顺序查找的排序方法
将一个记录插入一个已经排好序的有序表L中,从而得到一个新的、记录数增加1的有序表
特点是:从2开始一个个判断是否比前一个元素要大,如果比前面的小的话就要以0单元为哨兵,从该元素的前一个位置往前查找,比它大的元素后移一位,直到找到比它小的元素,
此时这个比它小的元素的后一位的位置就是这个哨兵元素应该呆的地方啦。


平均情况下,直接插入排序的时间复杂度为O(n2)。 直接插入排序仅需要一个记录的附加空间。所以空间复杂度为O(1).
2.折半插入排序:O(n*n)

3.希尔排序:不稳定的排序方法!!!
将记录序列分成若干子序列,分别对每个子序列进行插入排序。
且必须保证最后一次排序的增量d等于1,即对整个序列进行一次插入排序。


二、 快速排序:
其中,快速排序不稳定
1.起泡排序:O(n*n)
2.快速排序:不稳定的排序方法!!! O(nlogn)
每次都将最前面的那个元素当成是关键字进行排序。
设置low和high辅助比较和对换
首先对无序的记录序列进行“一次快速排序”,之后分别对分割所得两个子序列“递归”进行快速排序。

时间复杂度分析:
若待排记录的初始状态为按关键字有序时,快速排序将蜕化为起泡排序,其时间复杂度为O(n2)。
三、选择排序
1.简单选择排序:O(n*n)

分析比较次数:
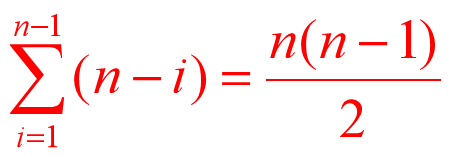
2.树型选择排序:O(nlogn)
首先对n个记录的关键字进行两两比较,然后在其中「n/2]个较小者之间再进行两两比较,如此重复,直至选出最小关键字的记录为止。
分析空间:
该方法占用空间较多,除需输出排序结果的n个单元外,尚需n-1个辅助单元。
3.堆排序:是不稳定的排序方法!!!O(nlogn)


四、归并排序
就是将两个或两个以上的有序表结合成一个新的有序表。
五、基数排列
1.多关键字的排列
分为MSD和LSD
前者是最高位优先行排列,需要分子序列
后者是最低位优先法,不需要进行子序列分配,而是直接对每个关键字都是整个序列参加排序
当对多关键字的记录序列进行LSD方法排序时,必须采用稳定的排序方法。
2.链式基数排列



总结:各种排序方法的分析
时间性能:
1.平均的时间性能
O(n*n)的称为简单排序方法,O(nlogn)的称为高效排序方法,O(dn)的称为基数排序方法

2.当待排序列关于关键字有序时:

3.

空间性能:(指的是所需要的辅助空间大小)


不稳定排序:
快速排序、希尔排序、堆排序:三个都是不稳定排序方法