20180525小测

T1:

简述一下题意，就是每天给你预算和一个点，让你用这个点到1的路径上的点做完全背包，问最大收益。
点数询问数<=5000，预算<=20000，时间限制1s，空间限制20Mb。
注意考试时是没有给预算的正确数据范围的，题意也不是很清晰，然后就弃疗了......(题意不明怪我喽)
考虑暴力怎么做，我们可以大力完全背包，时间空间复杂度都是O(ne)的。
可是显然会MLE啊......
考虑用时间换空间(计算机比你想象的快到不知道哪里去了)，如果我们能把空间复杂度的n优化为logn，时间复杂度再多个log也没事啊。
我们可以？树上cdq分治。
首先将询问离线，把询问全都放到点上。
考虑我们的分治结构，为树上的一个子联通块，我们已知这个联通块最高点到根的背包值。然后如何处理？
我们找出块重心，先递归包含最高点的部分。
然后暴力用重心到最高点的一条链上的权值和最高点的背包值求出重心的背包值，处理重心上的询问。
最后枚举重心的孩子，暴力处理出其背包值，然后递归计算。
时间复杂度O(nelogn)，由于最多递归logn层，所以空间复杂度O(elogn)。
代码:

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<algorithm>
 4 #include<vector>
 5 const int maxn=5e3+1e2,maxe=2e4+1e2;
 6 const int inf=0x3f3f3f3f;
 7 
 8 struct Query{ int siz,id; };
 9 int s[maxn],t[maxn<<1],nxt[maxn<<1],fa[maxn];
10 int cst[maxn],val[maxn],f[17][maxe];
11 int siz[maxn],mxs[maxn],ban[maxn];
12 int ans[maxn];
13 std::vector<Query> qs[maxn];
14 
15 inline void addedge(int from,int to) {
16     static int cnt;
17     t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt;
18 }
19 inline void trans(int* dst,const int &cst,const int &val) {
20     for(int i=cst;i<maxe;i++) dst[i] = std::max( dst[i] , dst[i-cst] + val );
21 }
22 
23 inline void getrt(int pos,int fa,const int &fs,int &rt) {
24     siz[pos] = 1 , mxs[pos] = 0;
25     for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa && !ban[t[at]] ) getrt(t[at],pos,fs,rt) , siz[pos] += siz[t[at]] , mxs[pos] = std::max( mxs[pos] , siz[t[at]] );
26     if( ( mxs[pos] = std::max( mxs[pos] , fs - siz[pos]) ) < mxs[rt] ) rt = pos;
27 }
28 inline void solve(int pos,int fs,int dep) { // pos is the highest point in this block , assert we know dp[pos] in f[dep].
29     if( fs == 1 ) {
30         for(unsigned i=0;i<qs[pos].size();i++) ans[qs[pos][i].id] = f[dep][qs[pos][i].siz];
31         return void(ban[pos]=1);
32     }
33     int rt = 0;
34     *mxs = inf , getrt(pos,-1,fs,rt) , ban[rt] = 1;
35     if( rt != pos ) memcpy(f[dep+1],f[dep],sizeof(f[0])) , solve(pos,fs-siz[rt],dep+1);
36     for(int i=rt;i!=pos;i=fa[i]) trans(f[dep],cst[i],val[i]);
37     for(unsigned i=0;i<qs[rt].size();i++) ans[qs[rt][i].id] = f[dep][qs[rt][i].siz];
38     for(int at=s[rt];at;at=nxt[at]) if( !ban[t[at]] ) memcpy(f[dep+1],f[dep],sizeof(f[0])) , trans(f[dep+1],cst[t[at]],val[t[at]]) , solve(t[at],siz[t[at]],dep+1);
39 }
40 
41 int main() {
42     static int n,m;
43     scanf("%d%d",&n,&m);
44     for(int i=1;i<=n;i++) scanf("%d%d",cst+i,val+i);
45     for(int i=2;i<=n;i++) scanf("%d",fa+i) , addedge(fa[i],i) , addedge(i,fa[i]);
46     for(int i=1;i<=m;i++) scanf("%d",ans+i);
47     for(int i=1,pos;i<=m;i++) scanf("%d",&pos) , qs[pos].push_back((Query){ans[i],i}) , ans[i] = 0;
48     trans(f[1],cst[1],val[1]) , solve(1,n,1);
49     for(int i=1;i<=m;i++) printf("%d
",ans[i]);
50     return 0;
51 }

View Code

T2:

这都是什么东西啊......
考虑暴力，中间没有特殊值的可以线段树，前面的25分？n^2暴力吧，能不能过看脸了。
写了，拍了，没错，感觉稳了。
然后评测下来发现只有10分！然后发现我赋值min和赋值max打反了，对拍的暴力的主函数是粘过去的，也是错的......
于是身败名裂。
这件事告诉我们对拍的暴力不要粘贴正解中除了头文件、变量声明和IO优化(如果有)以外的任何东西。因为你永远不知道你会在哪里出错。
正解弃坑啦！
10分代码:

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<cstring>
  4 #include<algorithm>
  5 #include<tr1/unordered_set>
  6 #define debug cerr
  7 typedef long long int lli;
  8 using namespace std;
  9 
 10 int n,m;
 11 
 12 namespace SubTask1 {
 13     const int maxn=5e3+1e2;
 14     const lli inf=0x3f3f3f3f3f3f3f3fll;
 15     lli in[maxn];
 16     tr1::unordered_set<lli> ban;
 17     
 18     inline void initban() {
 19         lli cur = 23;
 20         for(int i=1;i<=17;i++) cur = cur * 10 + 3 , ban.insert(cur);
 21     }
 22     inline void apply_add(int l,int r,const lli &x) {
 23         for(int i=l;i<=r;i++) in[i] += x;
 24     }
 25     inline void apply_fil(int l,int r,const lli &x) {
 26         for(int i=l;i<=r;i++) in[i] = x;
 27     }
 28     inline lli query_sum(int l,int r) {
 29         lli ret = 0;
 30         for(int i=l;i<=r;i++) ret += in[i];
 31         return ret;
 32     }
 33     inline lli query_mi(int l,int r) {
 34         lli ret = inf;
 35         for(int i=l;i<=r;i++) ret = min( ret , in[i] );
 36         return ret;
 37     }
 38     inline lli query_mx(int l,int r) {
 39         lli ret = -inf;
 40         for(int i=l;i<=r;i++) ret = max( ret , in[i] );
 41         return ret;
 42     }
 43     inline bool judge_ban(int l,int r) {
 44         for(int i=l;i<=r;i++) if( ban.find(in[i]) != ban.end() ) return 1;
 45         return 0;
 46     }
 47     void main() {
 48         initban();
 49         for(int i=1;i<=n;i++) scanf("%lld",in+i);
 50         for(int i=1,o,l,r,x;i<=m;i++) {
 51             scanf("%d",&o);
 52             if( o == 1 ) scanf("%d",&x) , printf("%lld
",query_sum(x,x));
 53             else {
 54                 scanf("%d%d",&l,&r);
 55                 if( o == 2 || o == 3 ) {
 56                     scanf("%d",&x);
 57                     if( o == 2 ) apply_fil(l,r,x);
 58                     else if( o == 3 ) apply_add(l,r,x);
 59                 } else {
 60                     lli val;
 61                     if( o == 4 ) val = query_mi(l,r);
 62                     else if( o == 5 ) val = query_mx(l,r);
 63                     else if( o == 6 ) val = query_sum(l,r) / ( r - l + 1 );
 64                     apply_fil(l,r,val);
 65                 }
 66                 if( o == 2 || o == 3 || o == 6 ) while( judge_ban(l,r) ) apply_add(l,r,1);
 67             }
 68         }
 69     }
 70 }
 71 
 72 namespace SubTask2 {
 73     const int maxn=1e5+1e2;
 74     int in[maxn];
 75     struct SegmentTree {
 76         int l[maxn<<2],r[maxn<<2],lson[maxn<<2],rson[maxn<<2],cnt;
 77         lli lazy_add[maxn<<2],lazy_fil[maxn<<2],sum[maxn<<2],mi[maxn<<2],mx[maxn<<2];
 78         SegmentTree() { memset(lazy_fil,-1,sizeof(lazy_fil)) , cnt = 1; }
 79         inline void apply_add(int pos,const lli &x) {
 80             mi[pos] += x , mx[pos] += x , sum[pos] += x * ( r[pos] - l[pos] + 1 );
 81             if( ~lazy_fil[pos] ) lazy_fil[pos] += x;
 82             else lazy_add[pos] += x;
 83         }
 84         inline void apply_fil(int pos,const lli &x) {
 85             mi[pos] = mx[pos] = lazy_fil[pos] = x , sum[pos] = x * ( r[pos] - l[pos] + 1 );
 86             lazy_add[pos] = 0;
 87         }
 88         inline void push(int pos) { // two marks will not appear at the same time .
 89             if( ~lazy_fil[pos] ) apply_fil(lson[pos],lazy_fil[pos]) , apply_fil(rson[pos],lazy_fil[pos]) , lazy_fil[pos] = -1;
 90             if( lazy_add[pos] ) apply_add(lson[pos],lazy_add[pos]) , apply_add(rson[pos],lazy_add[pos]) , lazy_add[pos] = 0;
 91         }
 92         inline void maintain(int pos) {
 93             sum[pos] = sum[lson[pos]] + sum[rson[pos]] , mi[pos] = min( mi[lson[pos]] , mi[rson[pos]] ) , mx[pos] = max( mx[lson[pos]] , mx[rson[pos]] );
 94         }
 95         inline void build(int pos,int ll,int rr) {
 96             if( ( l[pos] = ll ) == ( r[pos] =  rr ) ) return void(sum[pos] = mi[pos] = mx[pos] = in[ll]);
 97             const int mid = ( ll + rr ) >> 1;
 98             build(lson[pos]=++cnt,ll,mid) , build(rson[pos]=++cnt,mid+1,rr) , maintain(pos);
 99         }
100         inline void update_fil(int pos,const int &ll,const int &rr,const lli &x) {
101             if( rr < l[pos] || r[pos] < ll ) return;
102             if( ll <= l[pos] && r[pos] <= rr ) return apply_fil(pos,x);
103             push(pos) , update_fil(lson[pos],ll,rr,x) , update_fil(rson[pos],ll,rr,x) , maintain(pos);
104         }
105         inline void update_add(int pos,const int &ll,const int &rr,const lli &x) {
106             if( rr < l[pos] || r[pos] < ll ) return;
107             if( ll <= l[pos] && r[pos] <= rr ) return apply_add(pos,x);
108             push(pos) , update_add(lson[pos],ll,rr,x) , update_add(rson[pos],ll,rr,x) , maintain(pos);
109         }
110         inline lli query_mi(int pos,const int &ll,const int &rr) {
111             if( ll <= l[pos] && r[pos] <= rr ) return mi[pos];
112             push(pos); const int mid = ( l[pos] + r[pos] ) >> 1;
113             if( rr <= mid ) return query_mi(lson[pos],ll,rr);
114             else if( ll > mid ) return query_mi(rson[pos],ll,rr);
115             else return min( query_mi(lson[pos],ll,rr) , query_mi(rson[pos],ll,rr) );
116         }
117         inline lli query_mx(int pos,const int &ll,const int &rr) {
118             if( ll <= l[pos] && r[pos] <= rr ) return mx[pos];
119             push(pos); const int mid = ( l[pos] + r[pos] ) >> 1;
120             if( rr <= mid ) return query_mx(lson[pos],ll,rr);
121             else if( ll > mid ) return query_mx(rson[pos],ll,rr);
122             else return max( query_mx(lson[pos],ll,rr) , query_mx(rson[pos],ll,rr) );
123         }
124         inline lli query_sum(int pos,const int &ll,const int &rr) {
125             if( ll <= l[pos] && r[pos] <= rr ) return sum[pos];
126             push(pos); const int mid = ( l[pos] + r[pos] ) >> 1;
127             if( rr <= mid ) return query_sum(lson[pos],ll,rr);
128             else if( ll > mid ) return query_sum(rson[pos],ll,rr);
129             else return query_sum(lson[pos],ll,rr) + query_sum(rson[pos],ll,rr);
130         }
131     }sgt;
132     void main() {
133         for(int i=1;i<=n;i++) scanf("%d",in+i);
134         sgt.build(1,1,n);
135         for(int i=1,o,l,r,x;i<=m;i++) {
136             scanf("%d",&o);
137             if( o == 1 ) scanf("%d",&x) , printf("%lld
",sgt.query_sum(1,x,x));
138             else {
139                 scanf("%d%d",&l,&r);
140                 if( o == 2 || o == 3 ) {
141                     scanf("%d",&x);
142                     if( o == 2 ) sgt.update_fil(1,l,r,x);
143                     else sgt.update_add(1,l,r,x);
144                 } else {
145                     lli val;
146                     if( o == 4 ) val = sgt.query_mi(1,l,r);
147                     else if( o == 5 ) val = sgt.query_mx(1,l,r);
148                     else if( o == 6 ) val = sgt.query_sum(1,l,r) / ( r - l + 1 );
149                     sgt.update_fil(1,l,r,val);
150                 }
151             }
152         }
153     }
154 }
155 
156 int main() {
157     scanf("%d%d",&n,&m);
158     if( n <= 4000 && m <= 4000 ) SubTask1::main();
159     else SubTask2::main();
160     return 0;
161 }

View Code

50分暴力代码:

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<cstring>
  4 #include<algorithm>
  5 #include<tr1/unordered_set>
  6 #define debug cerr
  7 typedef long long int lli;
  8 using namespace std;
  9 
 10 int n,m;
 11 
 12 namespace SubTask1 {
 13     const int maxn=5e3+1e2;
 14     const lli inf=0x3f3f3f3f3f3f3f3fll;
 15     lli in[maxn];
 16     tr1::unordered_set<lli> ban;
 17     
 18     inline void initban() {
 19         lli cur = 23;
 20         for(int i=1;i<=17;i++) cur = cur * 10 + 3 , ban.insert(cur);
 21     }
 22     inline void apply_add(int l,int r,const lli &x) {
 23         for(int i=l;i<=r;i++) in[i] += x;
 24     }
 25     inline void apply_fil(int l,int r,const lli &x) {
 26         for(int i=l;i<=r;i++) in[i] = x;
 27     }
 28     inline lli query_sum(int l,int r) {
 29         lli ret = 0;
 30         for(int i=l;i<=r;i++) ret += in[i];
 31         return ret;
 32     }
 33     inline lli query_mi(int l,int r) {
 34         lli ret = inf;
 35         for(int i=l;i<=r;i++) ret = min( ret , in[i] );
 36         return ret;
 37     }
 38     inline lli query_mx(int l,int r) {
 39         lli ret = -inf;
 40         for(int i=l;i<=r;i++) ret = max( ret , in[i] );
 41         return ret;
 42     }
 43     inline bool judge_ban(int l,int r) {
 44         for(int i=l;i<=r;i++) if( ban.find(in[i]) != ban.end() ) return 1;
 45         return 0;
 46     }
 47     void main() {
 48         initban();
 49         for(int i=1;i<=n;i++) scanf("%lld",in+i);
 50         for(int i=1,o,l,r,x;i<=m;i++) {
 51             scanf("%d",&o);
 52             if( o == 1 ) scanf("%d",&x) , printf("%lld
",query_sum(x,x));
 53             else {
 54                 scanf("%d%d",&l,&r);
 55                 if( o == 2 || o == 3 ) {
 56                     scanf("%d",&x);
 57                     if( o == 2 ) apply_fil(l,r,x);
 58                     else if( o == 3 ) apply_add(l,r,x);
 59                 } else {
 60                     lli val;
 61                     if( o == 4 ) val = query_mx(l,r);
 62                     else if( o == 5 ) val = query_mi(l,r);
 63                     else if( o == 6 ) val = query_sum(l,r) / ( r - l + 1 );
 64                     apply_fil(l,r,val);
 65                 }
 66                 if( o == 2 || o == 3 || o == 6 ) while( judge_ban(l,r) ) apply_add(l,r,1);
 67             }
 68         }
 69     }
 70 }
 71 
 72 namespace SubTask2 {
 73     const int maxn=1e5+1e2;
 74     int in[maxn];
 75     struct SegmentTree {
 76         int l[maxn<<2],r[maxn<<2],lson[maxn<<2],rson[maxn<<2],cnt;
 77         lli lazy_add[maxn<<2],lazy_fil[maxn<<2],sum[maxn<<2],mi[maxn<<2],mx[maxn<<2];
 78         SegmentTree() { memset(lazy_fil,-1,sizeof(lazy_fil)) , cnt = 1; }
 79         inline void apply_add(int pos,const lli &x) {
 80             mi[pos] += x , mx[pos] += x , sum[pos] += x * ( r[pos] - l[pos] + 1 );
 81             if( ~lazy_fil[pos] ) lazy_fil[pos] += x;
 82             else lazy_add[pos] += x;
 83         }
 84         inline void apply_fil(int pos,const lli &x) {
 85             mi[pos] = mx[pos] = lazy_fil[pos] = x , sum[pos] = x * ( r[pos] - l[pos] + 1 );
 86             lazy_add[pos] = 0;
 87         }
 88         inline void push(int pos) { // two marks will not appear at the same time .
 89             if( ~lazy_fil[pos] ) apply_fil(lson[pos],lazy_fil[pos]) , apply_fil(rson[pos],lazy_fil[pos]) , lazy_fil[pos] = -1;
 90             if( lazy_add[pos] ) apply_add(lson[pos],lazy_add[pos]) , apply_add(rson[pos],lazy_add[pos]) , lazy_add[pos] = 0;
 91         }
 92         inline void maintain(int pos) {
 93             sum[pos] = sum[lson[pos]] + sum[rson[pos]] , mi[pos] = min( mi[lson[pos]] , mi[rson[pos]] ) , mx[pos] = max( mx[lson[pos]] , mx[rson[pos]] );
 94         }
 95         inline void build(int pos,int ll,int rr) {
 96             if( ( l[pos] = ll ) == ( r[pos] =  rr ) ) return void(sum[pos] = mi[pos] = mx[pos] = in[ll]);
 97             const int mid = ( ll + rr ) >> 1;
 98             build(lson[pos]=++cnt,ll,mid) , build(rson[pos]=++cnt,mid+1,rr) , maintain(pos);
 99         }
100         inline void update_fil(int pos,const int &ll,const int &rr,const lli &x) {
101             if( rr < l[pos] || r[pos] < ll ) return;
102             if( ll <= l[pos] && r[pos] <= rr ) return apply_fil(pos,x);
103             push(pos) , update_fil(lson[pos],ll,rr,x) , update_fil(rson[pos],ll,rr,x) , maintain(pos);
104         }
105         inline void update_add(int pos,const int &ll,const int &rr,const lli &x) {
106             if( rr < l[pos] || r[pos] < ll ) return;
107             if( ll <= l[pos] && r[pos] <= rr ) return apply_add(pos,x);
108             push(pos) , update_add(lson[pos],ll,rr,x) , update_add(rson[pos],ll,rr,x) , maintain(pos);
109         }
110         inline lli query_mi(int pos,const int &ll,const int &rr) {
111             if( ll <= l[pos] && r[pos] <= rr ) return mi[pos];
112             push(pos); const int mid = ( l[pos] + r[pos] ) >> 1;
113             if( rr <= mid ) return query_mi(lson[pos],ll,rr);
114             else if( ll > mid ) return query_mi(rson[pos],ll,rr);
115             else return min( query_mi(lson[pos],ll,rr) , query_mi(rson[pos],ll,rr) );
116         }
117         inline lli query_mx(int pos,const int &ll,const int &rr) {
118             if( ll <= l[pos] && r[pos] <= rr ) return mx[pos];
119             push(pos); const int mid = ( l[pos] + r[pos] ) >> 1;
120             if( rr <= mid ) return query_mx(lson[pos],ll,rr);
121             else if( ll > mid ) return query_mx(rson[pos],ll,rr);
122             else return max( query_mx(lson[pos],ll,rr) , query_mx(rson[pos],ll,rr) );
123         }
124         inline lli query_sum(int pos,const int &ll,const int &rr) {
125             if( ll <= l[pos] && r[pos] <= rr ) return sum[pos];
126             push(pos); const int mid = ( l[pos] + r[pos] ) >> 1;
127             if( rr <= mid ) return query_sum(lson[pos],ll,rr);
128             else if( ll > mid ) return query_sum(rson[pos],ll,rr);
129             else return query_sum(lson[pos],ll,rr) + query_sum(rson[pos],ll,rr);
130         }
131     }sgt;
132     void main() {
133         for(int i=1;i<=n;i++) scanf("%d",in+i);
134         sgt.build(1,1,n);
135         for(int i=1,o,l,r,x;i<=m;i++) {
136             scanf("%d",&o);
137             if( o == 1 ) scanf("%d",&x) , printf("%lld
",sgt.query_sum(1,x,x));
138             else {
139                 scanf("%d%d",&l,&r);
140                 if( o == 2 || o == 3 ) {
141                     scanf("%d",&x);
142                     if( o == 2 ) sgt.update_fil(1,l,r,x);
143                     else sgt.update_add(1,l,r,x);
144                 } else {
145                     lli val;
146                     if( o == 4 ) val = sgt.query_mx(1,l,r);
147                     else if( o == 5 ) val = sgt.query_mi(1,l,r);
148                     else if( o == 6 ) val = sgt.query_sum(1,l,r) / ( r - l + 1 );
149                     sgt.update_fil(1,l,r,val);
150                 }
151             }
152         }
153     }
154 }
155 
156 int main() {
157     scanf("%d%d",&n,&m);
158     if( n <= 4000 && m <= 4000 ) SubTask1::main();
159     else SubTask2::main();
160     return 0;
161 }

View Code

T3:

感觉这次考试唯一的一道好题......
题意就是要你造出一棵生成树满足权值最小，数据中所有数字非负。
什么为什么是树？因为不是树显然不优啊。
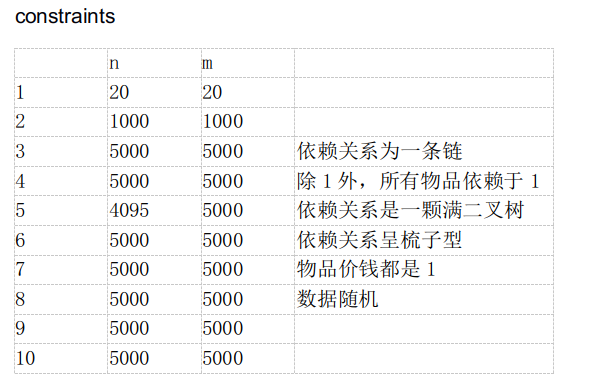
这种提交答案题首先要观察数据发现特殊性质，然后分类。
我分了如下几类：

测试点0本来就是一棵树，直接顺序输出即可。
代码:

1 #include<bits/stdc++.h>
2 
3 int main() {
4     int n,m;
5     scanf("%d%d",&n,&m);
6     for(int i=1;i<=m;i++) printf("%d
",i);
7     return 0;
8 }

View Code

测试点1最多有一个环，tarjan缩一发边双然后枚举删边(然而数据其实是一个大环，所以只有一个边双)。
代码:

 1 #include<bits/stdc++.h>
 2 #define debug cerr
 3 typedef long long int lli;
 4 using namespace std;
 5 const int maxn=1e6+1e2;
 6 
 7 map<lli,int> app;
 8 int s[maxn],t[maxn<<1],nxt[maxn<<1];
 9 int dfn[maxn],low[maxn],stk[maxn],ins[maxn],vis[maxn],ban[maxn],top; // ban will be 1 if bridge .
10 lli val[maxn],col[maxn],su,cv=0x3f3f3f3f3f3f3f3f;
11 int n,m,ans;
12 
13 inline void coredge(int from,int to) {
14     static int cnt = 1;
15     t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt;
16 }
17 inline void addedge(int a,int b) {
18     coredge(a,b) , coredge(b,a);
19 }
20 
21 inline void dfs(int pos,int fae) {
22     static int dd;
23     vis[pos] = 1 , low[pos] = dfn[pos] = ++dd;
24     for(int at=s[pos];at;at=nxt[at]) if( at != ( fae ^ 1 ) ) {
25         if( !vis[t[at]] ) {
26             dfs(t[at],at) , low[pos] = min( low[pos] , low[t[at]] );
27             if( low[t[at]] > dfn[pos] ) ban[at>>1] = 1;
28         } else low[pos] = min( low[pos] , dfn[t[at]] );
29     }
30 }
31 
32 inline lli calc(int edg) {
33     lli cs = app.size() - ( app[col[edg]] == 1 );
34     return ( su - val[edg] ) * cs;
35 }
36 
37 int main() {
38     scanf("%d%d",&n,&m);
39     for(int i=1,a,b;i<=m;i++) scanf("%d%d%lld%d",&a,&b,val+i,col+i) , addedge(a,b) , ++app[col[i]] , su += val[i];
40     dfs(1,0);
41     for(int i=1;i<=m;i++) {
42         if( !ban[i] && calc(i) <= cv ) cv =  calc(i) , ans = i;
43     }
44     for(int i=1;i<=m;i++) if( i != ans ) printf("%d
",i);
45     return 0;
46 }

View Code

测试点2只有一种颜色，最接最小生成树。
代码:

 1 #include<bits/stdc++.h>
 2 typedef long long int lli;
 3 using namespace std;
 4 const int maxn=1e5+1e2,maxe=1e6+1e2;
 5 
 6 int n,m;
 7 lli ans;
 8 
 9 struct Edge {
10     int u,v,id;
11     lli w;
12     friend bool operator < (const Edge &a,const Edge &b) {
13         return a.w < b.w;
14     }
15 }es[maxe];
16 
17 struct UnionFindSet {
18     int fa[maxn];
19     inline int findfa(int x) {
20         return fa[x] == x ? x : fa[x] = findfa(fa[x]);
21     }
22     inline bool merge(int x,int y) {
23         x = findfa(x) , y = findfa(y);
24         return x == y ? 0 : fa[x] = y;
25     }
26     inline void init() {
27         for(int i=1;i<=n;i++) fa[i] = i;
28     }
29 }ufs;
30 
31 int main() {
32     scanf("%d%d",&n,&m) , ufs.init();
33     for(int i=1;i<=m;i++) scanf("%d%d%lld%*d",&es[i].u,&es[i].v,&es[i].w) , es[i].id = i;
34     sort(es+1,es+1+m);
35     for(int i=1;i<=m;i++) if( ufs.merge(es[i].u,es[i].v) ) ans += es[i].w , printf("%d
",es[i].id);
36     return 0;
37 }

View Code

测试点3，5的颜色都比较少，我们可以状压枚举颜色然后最小生成树(测试点3编译选项Ofast优化全开，台式6代i5跑了半个小时QAQ)。
代码:

 1 #include<bits/stdc++.h>
 2 typedef long long int lli;
 3 using namespace std;
 4 const int maxn=1e5+1e2,maxe=1e6+1e2;
 5 const lli inf=0x3f3f3f3f3f3f3f3fll;
 6 
 7 int n,m;
 8 lli ans=inf;
 9 set<int> cs;
10 int way[maxe],mem[maxe];
11 
12 struct Edge {
13     int u,v,col,id;
14     lli w;
15     friend bool operator < (const Edge &a,const Edge &b) {
16         return a.w < b.w;
17     }
18 }es[maxe];
19 
20 struct UnionFindSet {
21     int fa[maxn];
22     inline int findfa(int x) {
23         return fa[x] == x ? x : fa[x] = findfa(fa[x]);
24     }
25     inline bool merge(int x,int y) {
26         x = findfa(x) , y = findfa(y);
27         return x == y ? 0 : fa[x] = y;
28     }
29     inline void init() {
30         for(int i=1;i<=n;i++) fa[i] = i;
31     }
32 }ufs;
33 
34 inline int getsiz(int x) {
35     int ret = 0;
36     while(x) ++ret , x -= (x&-x);
37     return ret;
38 }
39 inline lli calc(int sta) {
40     lli ret = 0 , sel = 0; ufs.init();
41     for(int i=1;i<=m;i++) if( ( es[i].col & sta ) && ufs.merge(es[i].u,es[i].v) ) ret += es[i].w , way[++sel]=i;
42     return sel == n - 1 ? ret * getsiz(sta) : inf;
43 }
44 
45 
46 int main() {
47     scanf("%d%d",&n,&m) , ufs.init();
48     for(int i=1;i<=m;i++) scanf("%d%d%lld%d",&es[i].u,&es[i].v,&es[i].w,&es[i].col) , es[i].col = 1 << ( es[i].col - 1 ) , cs.insert(es[i].col) , es[i].id = i;
49     sort(es+1,es+1+m);
50     int ss = 1 << cs.size();
51     cerr<<"inf = "<<inf<<endl;
52     for(int i=1;i<=m;i++) if( es[i].col >= ss ) cerr<<"color size error!"<<endl , exit(0);
53     for(int i=0;i<ss;i++) {
54         lli cal = calc(i);
55         if( cal < ans ) ans = cal , memcpy(mem,way,sizeof(int)*n) , cerr<<"copy i = "<<i<<endl;
56     }
57     for(int i=1;i<n;i++) printf("%d
",es[mem[i]].id);
58     return 0;
59 }

View Code

剩下的测试点(4,6,7,8,9)没发现啥特殊性质，直接上模拟退火(随机数种子？当然是我老婆的名字啦)。
代码:

 1 #include<bits/stdc++.h>
 2 typedef long long int lli;
 3 using namespace std;
 4 const int maxn=1e3+1e2,maxe=1e4+1e2;
 5 const lli inf=0x3f3f3f3f3f3f3f3fll;
 6 const double eps=1e-5,mul=0.9999,lambda=0.1,ini=1e8;
 7 
 8 int n,m;
 9 
10 struct UnionFindSet {
11     int fa[maxn];
12     inline int findfa(int x) {
13         return fa[x] == x ? x : fa[x] = findfa(fa[x]);
14     }
15     inline bool merge(int x,int y) {
16         x = findfa(x) , y = findfa(y);
17         return x == y ? 0 : fa[x] = y;
18     }
19     inline void init() {
20         for(int i=1;i<=n;i++) fa[i] = i;
21     }
22 }ufs;
23 
24 struct Edge {
25     int u,v,val,col,id;
26 }es[maxe];
27 
28 int cur[maxe],now[maxe],ans[maxe];
29 lli calc_cur,calc_now,calc_ans;
30 double temp;
31 
32 inline lli calc() {
33     set<int> cs; lli su = 0; ufs.init();
34     for(int t=1;t<=m;t++) {
35         const int i = cur[t];
36         if( ufs.merge(es[i].u,es[i].v) ) su += es[i].val , cs.insert(es[i].col);
37     }
38     return su * cs.size();
39 }
40 inline void printans() {
41     ufs.init();
42     for(int t=1;t<=m;t++) {
43         const int i = ans[t];
44         if( ufs.merge(es[i].u,es[i].v) ) printf("%d
",es[i].id);
45     }
46 }
47 inline void solve() {
48     memcpy(cur+1,now+1,sizeof(int)*m) , random_shuffle(cur+1,cur+1+m) , calc_cur = calc();
49     if( calc_cur < calc_ans ) memcpy(ans+1,cur+1,sizeof(int)*m) , calc_ans = calc_cur;
50     if( calc_cur < calc_now || ( temp > lambda && (double) rand() / ( rand() + 1 ) > temp ) ) memcpy(now+1,cur+1,sizeof(int)*m) , calc_now = calc_cur;
51 }
52 inline void random_seq() {
53     int l = rand() % m + 1 , r = rand() % m + 1;
54     if( l > r ) swap(l,r);
55     random_shuffle(cur+l,cur+r+1);
56 }
57 inline void solve2() {
58     memcpy(cur+1,now+1,sizeof(int)*m) , random_seq() , calc_cur = calc();
59     if( calc_cur < calc_ans ) memcpy(ans+1,cur+1,sizeof(int)*m) , calc_ans = calc_cur;
60     if( calc_cur < calc_now || ( temp > lambda && (double) rand() / ( rand() + 1 ) > temp ) ) memcpy(now+1,cur+1,sizeof(int)*m) , calc_now = calc_cur;
61 
62 }
63 inline void getans() {
64     calc_now = calc_ans = inf;
65     for(int i=1;i<=m;i++) now[i] = i;
66     for(temp=ini;temp>eps;temp*=mul) solve();
67     for(int i=1;i<=m;i++) now[i] = i;
68     calc_now = inf;
69     for(temp=ini;temp>eps;temp*=mul) solve2();
70 }
71 
72 
73 inline void init() { // it can work 
74     static const char seed[] = "KurenaiKisaragi";
75     uint su = 0 , li = strlen(seed);
76     for(uint i=0;i<li;i++) su += seed[i];
77     srand(su);
78 }
79 
80 int main() {
81     scanf("%d%d",&n,&m) , init();
82     for(int i=1;i<=m;i++) scanf("%d%d%d%d",&es[i].u,&es[i].v,&es[i].val,&es[i].col) , es[i].id = i;
83     getans() , printans();
84     return 0;
85 }

View Code

结果下来测试点0,1,2,3,5,7都A了，4,6挂得很惨，8,9的分数不算太低。
这题总分数下来全场第三，比两个学弟低不少(人家一个随机爬山爬到收敛，一个枚举选边颜色蒙特卡洛跑半个小时，好像还商量了(商量还行？))。
其实测试点4，6的颜色都比较少，正解都是先钦定割边必选然后爆搜颜色+剪枝(你测试点1写的tarjan怎么不知道拿过来用了？)。
依旧没有rank1(什么提答大战你这种续命选手还想rank1？)，然而也没有办法啦。考挂自己菜......

为什么没歌词了？额......改天再补嘛。
(这都能拖延？我还是快滚粗吧)

相关阅读:
log4j（四）——如何控制不同风格的日志信息的输出？
log4j（三）——如何控制不同级别的日志信息的输出？
log4j（二）——如何控制日志信息的输出？
【完全开源】知乎日报UWP版：增加Live磁贴、Badge、以及Toast通知
 【完全开源】知乎日报UWP版：项目结构说明、关键源代码解释
 【完全开源】知乎日报UWP版（下篇）：商店APP、github源码、功能说明。Windows APP 良心出品。
UWP开发：APP之间的数据交互（以微信为例）
【完全开源】知乎日报UWP版（上篇）：界面设计、官方API分析
 【完全开源】博客园客户端UWP版带源码、带APP（下篇）
UWP开发之控件：用WebView做聊天框
原文地址：https://www.cnblogs.com/Cmd2001/p/9089836.html