国际惯例的题面: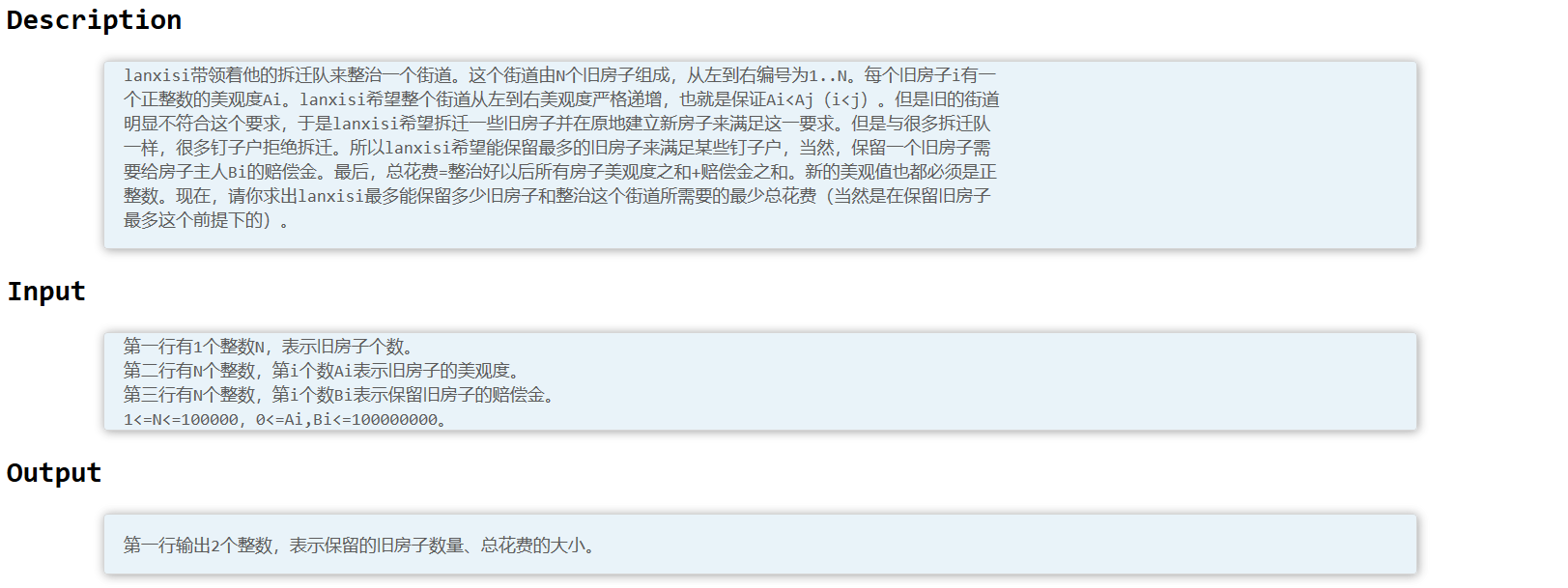
我们考虑大力DP。
首先重新定义代价为:1e13*选择数量-(总高度+总补偿)。这样我们只需要一个long long就能维护。
然后重新定义高度为heighti - i,这样我们能选择高度相同的点,同时可以把无论如何也不会被选择的点扔掉(这样他们的高度<0)。
之后就是转移,我们枚举i前面的被选择的点j,我们要满足的东西有:hj<=hi。
考虑我们再次选择一个点会产生怎样的代价,显然最终的答案一定是一个阶梯状的东西,所以我们选择了i之后之后所有点的高度相对于仅选择j都会上升(hi-hj)。
于是我们就可以转移了,fi=max{fj+(hi-hj)*(n-i+1)}(hj<=hi)+cost[i],cost[i]为单点价值减去选i的补偿代价。于是你可以写对拍用的n^2暴力了。
仔细观察这个转移方程,显然是一个可斜率优化的方程,我们可以把hi当成x,把fi当成j,把(n-i+1)当成a,把1当成b,这样最优答案就是ax+by的形式了。
因为hi不满足单调性,所以我们需要set维护凸包
考虑到我们还有hj<=hi的限制,所以需要再套一层cdq分治......
注意:
cdq分治在排序的时候不能只排单一关键字,需要做双关键字排序,否则会导致一些能更新的东西无法更新。
然后发现你这么写并不能AC,因为常数太大......
代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<set> 6 #include<cmath> 7 #include<vector> 8 #define debug cout 9 typedef long long int lli; 10 using namespace std; 11 const int maxn=1e5+1e2; 12 const lli mul = 1e13+1e10; 13 14 namespace Convex { 15 int cmp; // 0 compare x , 1 compare slope . 16 struct Point { 17 lli x,y; 18 long double slop; 19 friend bool operator < (const Point &a,const Point &b) { 20 if( !cmp ) return a.x != b.x ? a.x < b.x : a.y < b.y; 21 return a.slop > b.slop; 22 } 23 friend Point operator - (const Point &a,const Point &b) { 24 return (Point){a.x-b.x,a.y-b.y}; 25 } 26 friend long double operator * (const Point &a,const Point &b) { 27 return (long double)a.x * b.y - (long double)b.x * a.y; 28 } 29 inline lli calc(lli a,lli b) const { 30 return a * x + b * y; 31 } 32 }; 33 set<Point> st; 34 35 inline void Pop_right(set<Point>::iterator nxt,const Point &p) { 36 set<Point>::iterator lst; 37 while(1) { 38 nxt = st.lower_bound(p); 39 lst = nxt , ++nxt; 40 if( nxt == st.end() ) return; 41 if( lst->x == p.x ) { 42 if( p.y > lst->y ) st.erase(lst); 43 else break; 44 } 45 else { 46 if( (*lst-p) * (*nxt-*lst) < 0 ) return; 47 st.erase(lst); 48 } 49 } 50 } 51 inline void Pop_left(set<Point>::iterator prv,const Point &p) { 52 set<Point>::iterator lst; 53 prv = st.lower_bound(p) , --prv; 54 if( prv == st.begin() && prv->x == p.x ) return void(st.erase(prv)); 55 while(prv!=st.begin()) { 56 prv = st.lower_bound(p) , --prv; 57 lst = prv , --prv; 58 if( p.x == lst->x ) { 59 if( p.y > lst->y ) st.erase(lst); 60 else break; 61 continue; 62 } 63 else { 64 if( (*lst-*prv) * (p-*lst) < 0 ) break; 65 st.erase(lst); 66 } 67 } 68 } 69 inline bool fail(const Point &p) { 70 set<Point>::iterator it = st.lower_bound((Point){p.x,0,0}); 71 if( it != st.end() && it->x == p.x ) { 72 if( it->y >= p.y ) return 1; // p is useless at all . 73 else return 0; // p must be on convex . 74 } 75 if( it != st.end() && it != st.begin() ) { 76 set<Point>::iterator prv = it; --prv; 77 if( ( p - *prv ) * (*it - p ) > 0 ) return 1; 78 } 79 return 0; 80 } 81 inline void insert(const Point &p) { 82 cmp = 0; 83 if( fail(p) ) return; 84 set<Point>::iterator prv,nxt,lst=st.lower_bound(p); 85 if(lst!=st.begin()) Pop_left(--lst,p); 86 lst=st.lower_bound(p); 87 if(lst!=st.end()) Pop_right(lst,p); 88 st.insert(p) , lst = st.find(p); 89 if(lst!=st.begin()) { 90 prv = lst , --prv; 91 Point x = *prv; 92 x.slop = (long double)( p.y - x.y ) / ( p.x - x.x ); 93 st.erase(prv) , st.insert(x); 94 } 95 nxt = lst = st.find(p) , ++nxt; 96 if(nxt!=st.end()) { 97 Point x = p , n = *nxt; 98 x.slop = (long double)( n.y - x.y ) / ( n.x - x.x ); 99 st.erase(lst) , st.insert(x); 100 } else { 101 Point x = p; 102 x.slop = -1e18; 103 st.erase(lst) , st.insert(x); 104 } 105 } 106 inline lli query(const lli &k) { 107 cmp = 1; 108 set<Point>::iterator it = st.lower_bound((Point){0,0,(long double)-k}); // it can't be st.end() if st isn't empty . 109 if( it==st.end() ) return 0; 110 lli ret = it->calc(k,1); 111 if( it != st.begin() ) { 112 --it; 113 ret = max( ret , it->calc(k,1) ); 114 } 115 ++it; if( ++it!=st.end() ) ret = max( ret , it->calc(k,1) ); 116 return ret; 117 } 118 inline void clear() { 119 st.clear() , cmp = 0; 120 } 121 } 122 123 lli ina[maxn],inb[maxn],f[maxn],cst[maxn],ans,add; // f[id] . 124 bool isl[maxn]; 125 int n; 126 127 int cmp; // 0 compare height , 1 compare id . 128 struct Node { 129 lli hei,id; 130 friend bool operator < (const Node &a,const Node &b) { 131 if( cmp ) return a.id != b.id ? a.id < b.id : a.hei < b.hei; 132 else return a.hei != b.hei ? a.hei < b.hei : a.id < b.id; 133 } 134 }ns[maxn]; 135 136 vector<Node> vec; 137 138 inline void solve(vector<Node> &vec) { 139 if( vec.size() <= 1 ) { 140 if( vec.size() ) f[vec[0].id] = max( f[vec[0].id] , cst[vec[0].id] ); 141 return; 142 } 143 vector<Node> vl,vr; 144 const unsigned mid = vec.size() >> 1; 145 for(unsigned i=0;i<mid;i++) vl.push_back(vec[i]); 146 for(unsigned i=mid;i<vec.size();i++) vr.push_back(vec[i]); 147 solve(vl); 148 for(unsigned i=0;i<vl.size();i++) isl[vl[i].id] = 1; 149 for(unsigned i=0;i<vr.size();i++) isl[vr[i].id] = 0; 150 cmp = 1 , sort(vec.begin(),vec.end()) , Convex::clear(); 151 for(unsigned i=0;i<vec.size();i++) { 152 if( isl[vec[i].id] ) { 153 Convex::insert((Convex::Point){vec[i].hei,f[vec[i].id],0}); 154 } else { 155 f[vec[i].id] = max( f[vec[i].id] , cst[vec[i].id] + Convex::query(n-vec[i].id+1)); 156 } 157 } 158 solve(vr); 159 } 160 161 int main() { 162 static lli sel,lst; 163 scanf("%d",&n) , add = (lli) n * ( n + 1 ) >> 1; 164 for(int i=1;i<=n;i++) scanf("%lld",ina+i) , ina[i] -= i; 165 for(int i=1;i<=n;i++) { 166 scanf("%lld",inb+i); 167 if( ina[i] >= 0 ) { 168 cst[i] = mul - inb[i] - ina[i] * ( n - i + 1 ) , 169 vec.push_back((Node){ina[i],i}); 170 } 171 } 172 cmp = 0 , sort(vec.begin(),vec.end()); 173 solve(vec); 174 for(int i=1;i<=n;i++) ans = max( ans , f[i] ); 175 ans -= add; 176 sel = ( ans + mul ) / mul; 177 lst = mul * sel - ans; 178 printf("%lld %lld ",sel,lst); 179 return 0; 180 }
另外这个东西其实不用平衡树维护凸包,如果你外层分治位置,内层分治height的话,height就会有序,这样只需要写一个普通凸包就好了......
在BZOJ上只有这样才能AC......//QAQ
代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 #define debug cout 7 typedef long long int lli; 8 typedef long double ldb; 9 using namespace std; 10 const int maxn=1e5+1e2; 11 const lli mul = 1e13 + 1e10; 12 13 14 struct Convex { 15 struct Point { 16 lli x,y; 17 friend Point operator - (const Point &a,const Point &b) { 18 return (Point){a.x-b.x,a.y-b.y}; 19 } 20 friend ldb operator * (const Point &a,const Point &b) { 21 return (ldb)a.x*b.y - (ldb)a.y*b.x; 22 } 23 friend lli operator ^ (const Point &a,const Point &b) { 24 return a.x * b.x + a.y * b.y; 25 } 26 }ps[maxn]; 27 int top; 28 inline void push(const Point &p) { 29 while( top > 1 ) { 30 if( p.x == ps[top].x && p.y > ps[top].y ) --top; 31 else if( ( ps[top] - ps[top-1] ) * ( p - ps[top] ) > 0 ) --top; 32 else break; 33 } 34 if( top == 1 && p.x == ps[top].x && p.y > ps[top].y ) --top; 35 if( !top || p.x != ps[top].x ) ps[++top] = p; 36 } 37 inline lli query(const Point &p) { 38 int l = 1 , r = top , lmid , rmid; 39 while( r > l + 2 ) { 40 lmid = ( l + l + r ) / 3 , rmid = ( l + r + r ) / 3; 41 if( ( p ^ ps[lmid] ) < ( p ^ ps[rmid] ) ) l = lmid; 42 else r = rmid; 43 } 44 lli ret = 0; 45 for(int i=l;i<=r;i++) ret = max( ret , p ^ ps[i] ); 46 return ret; 47 } 48 inline void clear() { 49 top = 0; 50 } 51 }con; 52 53 lli ina[maxn],inb[maxn],f[maxn],cst[maxn],ans,add; // f[id] . 54 bool isl[maxn]; 55 int n; 56 57 int cmp; // 0 compare height , 1 compare id . 58 struct Node { 59 lli hei,id; 60 friend bool operator < (const Node &a,const Node &b) { 61 if( cmp ) return a.id != b.id ? a.id < b.id : a.hei < b.hei; 62 else return a.hei != b.hei ? a.hei < b.hei : a.id < b.id; 63 } 64 }ns[maxn]; 65 66 vector<Node> vec; 67 68 inline void solve(vector<Node> &vec) { 69 if( vec.size() <= 1 ) { 70 if( vec.size() ) f[vec[0].id] = max( f[vec[0].id] , cst[vec[0].id] ); 71 return; 72 } 73 vector<Node> vl,vr; 74 const unsigned mid = vec.size() >> 1; 75 for(unsigned i=0;i<mid;i++) vl.push_back(vec[i]); 76 for(unsigned i=mid;i<vec.size();i++) vr.push_back(vec[i]); 77 solve(vl); 78 for(unsigned i=0;i<vl.size();i++) isl[vl[i].id] = 1; 79 for(unsigned i=0;i<vr.size();i++) isl[vr[i].id] = 0; 80 cmp = 0 , sort(vec.begin(),vec.end()) , con.clear(); 81 for(unsigned i=0;i<vec.size();i++) { 82 if( isl[vec[i].id] ) { 83 con.push((Convex::Point){vec[i].hei,f[vec[i].id]}); 84 } else { 85 f[vec[i].id] = max( f[vec[i].id] , cst[vec[i].id] + con.query((Convex::Point){n-vec[i].id+1,1})); 86 } 87 } 88 solve(vr); 89 } 90 91 int main() { 92 static lli sel,lst; 93 scanf("%d",&n) , add = (lli) n * ( n + 1 ) >> 1; 94 for(int i=1;i<=n;i++) scanf("%lld",ina+i) , ina[i] -= i; 95 for(int i=1;i<=n;i++) { 96 scanf("%lld",inb+i); 97 if( ina[i] >= 0 ) { 98 cst[i] = mul - inb[i] - ina[i] * ( n - i + 1 ) , 99 vec.push_back((Node){ina[i],i}); 100 } 101 } 102 cmp = 1 , sort(vec.begin(),vec.end()); 103 solve(vec); 104 for(int i=1;i<=n;i++) ans = max( ans , f[i] ); 105 ans -= add; 106 sel = ( ans + mul ) / mul; 107 lst = mul * sel - ans; 108 printf("%lld %lld ",sel,lst); 109 return 0; 110 }
