如果给你平面内一些点,让你求距离某一个指定点最近的点,应该怎么办呢?
O(n)遍历!
但是,在遍历的过程中,我们发现有一些点是永远无法更新答案的。
如果我们把这些点按照一定顺序整理起来,省略对不必要点的遍历,是不是可以降低时间复杂度呢?
这样的话,我们要用到的工具就是KDtree。
KDtree本质上是一颗BST(二叉搜索树),只不过每一层按照不同的维度分割,也就是说,一层划分x,一层划分y,交替进行。大概就是这样:
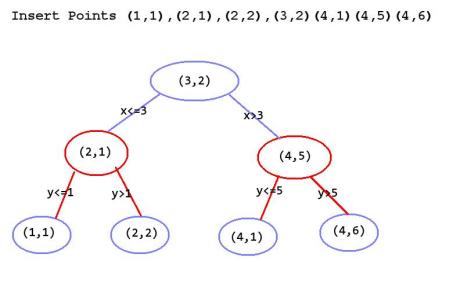
如果我们把他画在二维平面上的话,会发现KDtree实际上把一个矩形分割成了多个小矩形:
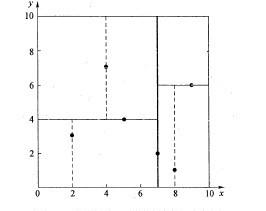
(我是来盗图的QAQ)
更新答案时,采用邻域搜索的方式。我们发现我们查询的点落在了某个小矩形内,我们用这个小矩形内的点去更新答案。然后进行回溯,看一下周围的矩形有没有可能存在更优答案,如果不可能的话,就不用搜索它了。
这样下来的复杂度最优是O(logn),随机数据介于O(logn)~O(sqrt(n))之间。如果是特意构造的数据,可以卡到O(n)(比如精度要求实数,给你一个圆,让你查询距离圆心最近的点)。
然而一般情况下KDtree比较好写,在考场上可以比较经济地拿到大部分分数,还是值得学习的。
关于代码实现,自己YY即可。反正我是脑补出来的。
例题:
BZOJ2716/2648:
KDtree查曼哈顿距离的板子,由于数据比较水所以直接插入可过,不需要考虑平衡性的问题。
代码自己YY。我的仅供参考(虽然我自行胡编的代码没什么参考价值QAQ)。
代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cstdlib> 6 using namespace std; 7 const int maxn=1.5e6+1e2; 8 const int inf=0x3f3f3f3f; 9 10 int cmp,ans; 11 struct Point { 12 int d[2]; 13 friend bool operator < (const Point &a,const Point &b) { 14 return a.d[cmp] < b.d[cmp]; 15 } 16 int dis(const Point &o) const { 17 int ret = 0; 18 for(int i=0;i<2;i++) 19 ret += abs( d[i] - o.d[i] ); 20 return ret; 21 } 22 }ps[maxn]; 23 24 int lson[maxn],rson[maxn],mi[maxn][2],mx[maxn][2]; 25 Point dv[maxn]; 26 int cnt; 27 28 inline void update(int pos) { 29 if( lson[pos] ) { 30 for(int i=0;i<2;i++) 31 mi[pos][i] = min( mi[pos][i] , mi[lson[pos]][i] ), 32 mx[pos][i] = max( mx[pos][i] , mx[lson[pos]][i] ); 33 } 34 if( rson[pos] ) { 35 for(int i=0;i<2;i++) 36 mi[pos][i] = min( mi[pos][i] , mi[rson[pos]][i] ), 37 mx[pos][i] = max( mx[pos][i] , mx[rson[pos]][i] ); 38 } 39 } 40 inline void fill(int pos,const Point &p) { 41 dv[pos] = p; 42 for(int i=0;i<2;i++) 43 mx[pos][i] = mi[pos][i] = p.d[i]; 44 } 45 inline void build(int pos,int pl,int pr,int dir) { 46 const int pmid = ( pl + pr ) >> 1; 47 cmp = dir; 48 nth_element(ps+pl,ps+pmid,ps+pr+1); 49 fill(pos,ps[pmid]); 50 if( pl < pmid ) build(lson[pos]=++cnt,pl,pmid-1,dir^1); 51 if( pr > pmid ) build(rson[pos]=++cnt,pmid+1,pr,dir^1); 52 update(pos); 53 } 54 inline void insert(int pos,Point np,int dir) { 55 cmp = dir; 56 if( np < dv[pos] ) { 57 if( lson[pos] ) insert(lson[pos],np,dir^1); 58 else { 59 lson[pos] = ++cnt; 60 fill(lson[pos],np); 61 } 62 } else { 63 if( rson[pos] ) insert(rson[pos],np,dir^1); 64 else { 65 rson[pos] = ++cnt; 66 fill(rson[pos],np); 67 } 68 } 69 update(pos); 70 } 71 inline int dis(int pos,const Point &p) { 72 int ret = 0; 73 for(int i=0;i<2;i++) 74 ret += max( p.d[i] - mx[pos][i] , 0 ) + max( mi[pos][i] - p.d[i] , 0 ); 75 return ret; 76 } 77 inline void query(int pos,const Point &p) { 78 ans = min( ans , p.dis(dv[pos]) ); 79 int dl = lson[pos] ? dis(lson[pos],p) : inf; 80 int dr = rson[pos] ? dis(rson[pos],p) : inf; 81 if( dl < dr ) { 82 if( dl < ans ) query(lson[pos],p); 83 if( dr < ans ) query(rson[pos],p); 84 } else { 85 if( dr < ans ) query(rson[pos],p); 86 if( dl < ans ) query(lson[pos],p); 87 } 88 } 89 90 int main() { 91 static int n,m; 92 static Point p; 93 94 scanf("%d%d",&n,&m); 95 for(int i=1;i<=n;i++) 96 scanf("%d%d",ps[i].d,ps[i].d+1); 97 98 build(cnt=1,1,n,0); 99 100 for(int i=1,t;i<=m;i++) { 101 scanf("%d%d%d",&t,p.d,p.d+1); 102 if(t == 1) { 103 insert(1,p,0); 104 } else { 105 ans = inf; 106 query(1,p); 107 printf("%d ",ans); 108 } 109 } 110 return 0; 111 }
BZOJ4066:
查询二维区间和。
本来这个题能够有多种做法,结果强制在线卡了cdq分治,20mb内存卡了树套树(什么你说你敢写?去写吧再见),其他一些奇奇怪怪的算法(分块线段树,分块splay之类的)并不是很容易实现。于是就只好KDtree了。
我们用KDtree上每一个节点去维护当前四边形的sum值,同时维护size。如果size过于不平衡了就进行重构(替罪羊树原理),同时手写内存池回收节点。
然而这样做并不能AC(怕不是我写搓了),需要在替罪羊重构的基础上判定一个修改次数,如果两次重构之间修改太少则不进行重构(否则不停地重构依旧TLE),另外你需要一个文件快读来保证AC。
另外如果这样写了仍不能AC,请注意调参,我用的是替罪羊的alpha设0.8,修改次数的lambda设1000,这样能够卡着50s的时限AC。
另外,如果实在TLE,那就弃了吧......
实在不明白为什么网上别人暴力重构和不重构能轻松AC。
代码:

1 #pragma GCC optimize(3) 2 #include<cstdio> 3 #include<algorithm> 4 #include<cctype> 5 using namespace std; 6 const int maxn=2e5+1e1; 7 const double alpha = 0.8; 8 9 int cmp; 10 struct Point { 11 int d[2],val; 12 friend bool operator < (const Point &a,const Point &b) { 13 return a.d[cmp] < b.d[cmp]; 14 } 15 friend bool operator == (const Point &a,const Point &b) { 16 return a.d[0] == b.d[0] && a.d[1] == b.d[1]; 17 } 18 Point operator += (const Point &x) { 19 val += x.val; 20 return *this; 21 } 22 inline void reset() { 23 d[0] = d[1] = val = 0; 24 } 25 }ps[maxn],nv[maxn]; 26 27 int lson[maxn],rson[maxn],mi[maxn][2],mx[maxn][2],sum[maxn],siz[maxn]; 28 int reb,delta,root; 29 30 namespace RamPool { 31 int pool[maxn],top; 32 inline void DelNode(int x) { 33 lson[x] = rson[x] = 0; 34 pool[++top] = x; 35 } 36 inline int NewNode() { 37 return pool[top--]; 38 } 39 } 40 41 using RamPool::DelNode;using RamPool::NewNode; 42 43 inline void update(int pos) { 44 sum[pos] = nv[pos].val; 45 if( lson[pos] ) { 46 for(int i=0;i<2;i++) 47 mi[pos][i] = min( mi[pos][i] , mi[lson[pos]][i] ), 48 mx[pos][i] = max( mx[pos][i] , mx[lson[pos]][i] ); 49 sum[pos] += sum[lson[pos]]; 50 } 51 if( rson[pos] ) { 52 for(int i=0;i<2;i++) 53 mi[pos][i] = min( mi[pos][i] , mi[rson[pos]][i] ), 54 mx[pos][i] = max( mx[pos][i] , mx[rson[pos]][i] ); 55 sum[pos] += sum[rson[pos]]; 56 } 57 } 58 inline void fill(int pos,const Point &p) { 59 nv[pos] = p , siz[pos] = 1; 60 for(int i=0;i<2;i++) 61 mi[pos][i] = mx[pos][i] = p.d[i]; 62 sum[pos] = p.val; 63 } 64 inline void build(int pos,int ll,int rr,int dir) { 65 cmp = dir; 66 const int mid = ( ll + rr ) >> 1; 67 nth_element(ps+ll,ps+mid,ps+rr+1); 68 fill(pos,ps[mid]); siz[pos] = rr - ll + 1; 69 if( ll < mid ) build(lson[pos]=NewNode(),ll,mid-1,dir^1); 70 if( rr > mid ) build(rson[pos]=NewNode(),mid+1,rr,dir^1); 71 update(pos); 72 } 73 inline void recycle(int pos,int& pcnt) { 74 if( lson[pos] ) recycle(lson[pos],pcnt); 75 if( rson[pos] ) recycle(rson[pos],pcnt); 76 ps[++pcnt] = nv[pos]; 77 DelNode(pos); 78 } 79 inline int rebuild(int pos,int dir) { 80 reb = 1; 81 int pcnt = 0; 82 recycle(pos,pcnt); 83 int ret = NewNode(); 84 build(ret,1,pcnt,dir); 85 return ret; 86 } 87 88 inline int insert(int pos,int dir,const Point &p) { 89 cmp = dir; 90 if( !nv[pos].val ) { 91 fill(pos,p); 92 return pos; 93 } 94 if( p == nv[pos] ) { 95 nv[pos] += p; 96 sum[pos] += p.val; 97 return pos; 98 } 99 ++siz[pos]; 100 if( p < nv[pos] ) { 101 if( !lson[pos] ) lson[pos] = NewNode(); 102 lson[pos] = insert(lson[pos],dir^1,p); 103 if( !reb && delta > 1000 && siz[lson[pos]] > (double) siz[pos] * alpha ) 104 return rebuild(pos,dir); 105 } else { 106 if( !rson[pos] ) rson[pos] = NewNode(); 107 rson[pos] = insert(rson[pos],dir^1,p); 108 if( !reb && delta > 1000 && siz[rson[pos]] > (double) siz[pos] * alpha ) 109 return rebuild(pos,dir); 110 } 111 update(pos); 112 return pos; 113 } 114 115 inline bool inside(const int &Insx,const int &Insy,const int &Intx,const int &Inty,const int &Osx,const int &Osy,const int &Otx,const int &Oty) { 116 return Osx <= Insx &&Intx <= Otx && Osy <= Insy &&Inty <= Oty; 117 } 118 inline bool outside(const int &Insx,const int &Insy,const int &Intx,const int &Inty,const int &Osx,const int &Osy,const int &Otx,const int &Oty) { 119 return Insx > Otx || Intx < Osx || Insy > Oty || Inty < Osy; 120 } 121 inline bool inside(const Point &p,const int &Osx,const int &Osy,const int &Otx,const int &Oty) { 122 return inside(p.d[0],p.d[1],p.d[0],p.d[1],Osx,Osy,Otx,Oty); 123 } 124 inline int query(int pos,const int &sx,const int &sy,const int &tx,int const &ty) { 125 if( outside(mi[pos][0],mi[pos][1],mx[pos][0],mx[pos][1],sx,sy,tx,ty) ) return 0; 126 if( inside(mi[pos][0],mi[pos][1],mx[pos][0],mx[pos][1],sx,sy,tx,ty) ) return sum[pos]; 127 int ret = 0; 128 if( inside(nv[pos],sx,sy,tx,ty) ) ret += nv[pos].val; 129 if( lson[pos] ) ret += query(lson[pos],sx,sy,tx,ty); 130 if( rson[pos] ) ret += query(rson[pos],sx,sy,tx,ty); 131 return ret; 132 } 133 134 inline void init() { 135 for(int i=1;i<maxn;i++) 136 DelNode(i); 137 root = NewNode(); 138 } 139 140 inline char nextchar() { 141 static char buf[1<<22],*st=buf+(1<<22),*ed=buf+(1<<22); 142 if( st == ed ) ed = buf + fread(st=buf,1,1<<22,stdin); 143 return st == ed ? -1 : *st++; 144 } 145 inline int getint() { 146 int ret = 0,ch; 147 while( !isdigit(ch=nextchar()) ); 148 do ret=ret*10+ch-'0'; while( isdigit(ch=nextchar()) ); 149 return ret; 150 } 151 152 int main() { 153 static int ope,lastans,sx,sy,tx,ty,xx,yy,num; 154 init(); 155 156 getint(); 157 while( ( ope = getint() ) != 3 ) { 158 if( ope == 1 ) { 159 xx = getint() , yy = getint() , num = getint(); 160 reb = 0 , ++delta; 161 xx ^= lastans , yy ^= lastans , num ^= lastans; 162 root = insert(root,0,(Point){xx,yy,num}); 163 } else { 164 sx = getint() , sy = getint() , tx = getint() , ty = getint(); 165 sx ^= lastans , sy ^= lastans , tx ^= lastans , ty ^= lastans; 166 printf("%d ", lastans = query(root,sx,sy,tx,ty) ); 167 } 168 } 169 170 return 0; 171 }
Upd20180104:
其实那个TLE是我替罪羊重构写的姿势不对了,正确的姿势是找到最浅的不平衡点进行重构,不需要判断size的。虽然这样还是比暴力重构慢,但好在能稳稳地AC了QAQ。
代码:

1 #pragma GCC optimize(3) 2 #include<cstdio> 3 #include<algorithm> 4 #include<cctype> 5 using namespace std; 6 const int maxn=2.5e5+1e2; 7 const double alpha=0.8; 8 9 int cmp; 10 struct Point { 11 int d[2],val; 12 Point(){} 13 Point(int xx,int yy,int vv) {d[0] = xx , d[1] = yy , val = vv;} 14 friend bool operator < (const Point &a,const Point &b) { 15 return a.d[cmp] < b.d[cmp]; 16 } 17 friend bool operator == (const Point &a,const Point &b) { 18 return a.d[0] == b.d[0] && a.d[1] == b.d[1]; 19 } 20 Point operator += (const Point &r) { 21 val += r.val; 22 return *this; 23 } 24 }ps[maxn],dv[maxn]; 25 struct QNode { 26 int mi[2],mx[2]; 27 QNode(int Mix,int Miy,int Mxx,int Mxy) { 28 mi[0] = Mix , mi[1] = Miy , mx[0] = Mxx , mx[1] = Mxy; 29 } 30 }; 31 int lson[maxn],rson[maxn],siz[maxn],mi[maxn][2],mx[maxn][2],sum[maxn]; 32 int root,rebp,rebfa,rebdir; 33 34 namespace RamPool { 35 int pool[maxn],top; 36 inline void DelNode(int x) { 37 siz[x] = lson[x] = rson[x] = 0; 38 pool[++top] = x; 39 } 40 inline int NewNode() { 41 return pool[top--]; 42 } 43 } 44 using RamPool::DelNode; using RamPool::NewNode; 45 46 inline void fill(int pos,const Point &p) { 47 dv[pos] = p , sum[pos] = p.val , siz[pos] = 1; 48 for(int i=0;i<2;i++) 49 mi[pos][i] = mx[pos][i] = p.d[i]; 50 } 51 inline void coreupdate(const int &fa,const int &son) { 52 sum[fa] += sum[son] , siz[fa] += siz[son]; 53 for(int i=0;i<2;i++) 54 mi[fa][i] = min( mi[fa][i] , mi[son][i] ) , 55 mx[fa][i] = max( mx[fa][i] , mx[son][i] ); 56 } 57 inline void update(int pos) { 58 sum[pos] = dv[pos].val , siz[pos] = 1; 59 if( lson[pos] ) 60 coreupdate(pos,lson[pos]); 61 if( rson[pos] ) 62 coreupdate(pos,rson[pos]); 63 } 64 inline void build(int pos,int ll,int rr,int dir) { 65 cmp = dir; 66 const int mid = ( ll + rr ) >> 1; 67 nth_element(ps+ll,ps+mid,ps+rr+1); 68 fill(pos,ps[mid]); 69 if( ll < mid ) build(lson[pos]=NewNode(),ll,mid-1,dir^1); 70 if( rr > mid ) build(rson[pos]=NewNode(),mid+1,rr,dir^1); 71 update(pos); 72 } 73 inline void recycle(int pos,int& pcnt) { 74 if( lson[pos] ) recycle(lson[pos],pcnt); 75 if( rson[pos] ) recycle(rson[pos],pcnt); 76 ps[++pcnt] = dv[pos]; 77 DelNode(pos); 78 } 79 inline int rebuild(int pos,int dir) { 80 int pcnt = 0; 81 recycle(pos,pcnt); 82 int ret = NewNode(); 83 build(ret,1,pcnt,dir); 84 return ret; 85 } 86 inline void insert(int pos,int dir,const Point &p) { 87 cmp = dir; 88 if( !dv[pos].val ) { 89 fill(pos,p); 90 return; 91 } 92 if( dv[pos] == p ) { 93 dv[pos] += p , sum[pos] += p.val; 94 return; 95 } 96 if( p < dv[pos] ) { 97 if( !lson[pos] ) lson[pos] = NewNode(); 98 insert(lson[pos],dir^1,p); 99 update(pos); 100 if( siz[lson[pos]] > siz[pos] * alpha ) rebp = pos , rebdir = dir , rebfa = 0; 101 else if( lson[pos] == rebp ) rebfa = pos; 102 } else { 103 if( !rson[pos] ) rson[pos] = NewNode(); 104 insert(rson[pos],dir^1,p); 105 update(pos); 106 if( siz[rson[pos]] > siz[pos] * alpha ) rebp = pos , rebdir = dir , rebfa = 0; 107 else if( rson[pos] == rebp ) rebfa = pos; 108 } 109 } 110 111 inline bool inside(const int* mi,const int* mx,const QNode &q) { 112 return q.mi[0] <= mi[0] && mx[0] <= q.mx[0] && q.mi[1] <= mi[1] && mx[1] <= q.mx[1]; 113 } 114 inline bool inside(const Point &p,const QNode &q) { 115 return inside(p.d,p.d,q); 116 } 117 inline bool inside(const int &pos,const QNode &q) { 118 return inside(mi[pos],mx[pos],q); 119 } 120 inline bool outside(const int* mi,const int* mx,const QNode &q) { 121 return mx[0] < q.mi[0] || q.mx[0] < mi[0] || mx[1] < q.mi[1] || q.mx[1] < mi[1]; 122 } 123 inline bool outside(const int &pos,const QNode &q) { 124 return outside(mi[pos],mx[pos],q); 125 } 126 inline int query(int pos,const QNode &q) { 127 if( outside(pos,q) ) return 0; 128 if( inside(pos,q) ) return sum[pos]; 129 int ret = 0; 130 if( inside(dv[pos],q) ) ret = dv[pos].val; 131 if( lson[pos] ) ret += query(lson[pos],q); 132 if( rson[pos] ) ret += query(rson[pos],q); 133 return ret; 134 } 135 136 inline void init() { 137 for(int i=maxn-1;i;i--) 138 DelNode(i); 139 root = NewNode(); 140 } 141 inline void rebuild() { 142 if( !rebfa ) root = rebuild(root,0); 143 else if( rebp == lson[rebfa] ) lson[rebfa] = rebuild(rebp,rebdir); 144 else rson[rebfa] = rebuild(rebp,rebdir); 145 } 146 147 inline char nextchar() { 148 static char buf[1<<21],*st=buf+(1<<21),*ed=buf+(1<<21); 149 if( st == ed ) ed = buf + fread(st=buf,1,1<<21,stdin); 150 return st != ed ? *st++ : -1; 151 } 152 inline int getint() { 153 int ret = 0 , ch; 154 while( !isdigit(ch=nextchar()) ); 155 do ret=ret*10+ch-'0'; while( isdigit(ch=nextchar()) ); 156 return ret; 157 } 158 159 int main() { 160 static int ope,xx,yy,add,sx,sy,tx,ty,lastans; 161 init(); 162 getint(); 163 while( ( ope = getint() ) != 3 ) { 164 if( ope == 1 ) { 165 xx = getint()^lastans , yy = getint()^lastans , add = getint()^lastans; 166 rebp = rebfa = rebdir = 0; 167 insert(root,0,Point(xx,yy,add)); 168 if( rebp ) rebuild(); 169 } else if( ope == 2 ) { 170 sx = getint()^lastans , sy = getint()^lastans , tx = getint()^lastans , ty = getint()^lastans; 171 printf("%d ", lastans = query( root , QNode(sx,sy,tx,ty) ) ); 172 } 173 } 174 175 return 0; 176 }
另外KDtree还有一道水题:
BZOJ2850:
让你求平面内ax+by<=c的点的权值和。没有插入只有查询……KDtree随便做一下就好了,看一看当前块是不是全部包含在可行范围内,如果全部包含则返回sum,如果全部不包含则返回0,否则递归查询子树。
这样的复杂度大概是log级的,考虑每次分成4块,最多往下递归3块,这样是log级的。
代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #define lli long long int 6 #define debug cout 7 using namespace std; 8 const int maxn=1e6+1e2; 9 10 int cmp; 11 struct Point { 12 lli d[2],h; 13 friend bool operator < (const Point &a,const Point &b) { 14 return a.d[cmp] < b.d[cmp]; 15 } 16 inline lli f(int a,int b) const { 17 return a * d[0] + b * d[1]; 18 } 19 }ps[maxn],dv[maxn]; 20 21 int lson[maxn],rson[maxn],cnt; 22 lli mx[maxn][2],mi[maxn][2],sum[maxn]; 23 lli c; 24 25 inline lli f(lli x,lli y,int a,int b) { 26 return a * x + b * y; 27 } 28 29 inline void update(int pos) { 30 if( lson[pos] ) { 31 for(int i=0;i<2;i++) 32 mi[pos][i] = min( mi[pos][i] , mi[lson[pos]][i] ), 33 mx[pos][i] = max( mx[pos][i] , mx[lson[pos]][i] ); 34 sum[pos] += sum[lson[pos]]; 35 } 36 if( rson[pos] ) { 37 for(int i=0;i<2;i++) 38 mi[pos][i] = min( mi[pos][i] , mi[rson[pos]][i] ), 39 mx[pos][i] = max( mx[pos][i] , mx[rson[pos]][i] ); 40 sum[pos] += sum[rson[pos]]; 41 } 42 } 43 inline void fill(int pos,const Point &p) { 44 dv[pos] = p; 45 for(int i=0;i<2;i++) 46 mx[pos][i] = mi[pos][i] = p.d[i]; 47 sum[pos] = p.h; 48 } 49 inline void build(int pos,int ll,int rr,int dir) { 50 cmp = dir; 51 const int mid = ( ll + rr ) >> 1; 52 nth_element(ps+ll,ps+mid,ps+rr+1); 53 fill(pos,ps[mid]); 54 if( ll < mid ) build(lson[pos]=++cnt,ll,mid-1,dir^1); 55 if( rr > mid ) build(rson[pos]=++cnt,mid+1,rr,dir^1); 56 update(pos); 57 } 58 inline int judge(int pos,int a,int b) { 59 return ( f(mx[pos][0],mx[pos][1],a,b) < c ) + ( f(mx[pos][0],mi[pos][1],a,b) < c ) + 60 ( f(mi[pos][0],mx[pos][1],a,b) < c ) + ( f(mi[pos][0],mi[pos][1],a,b) < c ) ; 61 } 62 inline lli query(int pos,int a,int b) { 63 lli ret = 0; 64 if( dv[pos].f(a,b) < c ) 65 ret += dv[pos].h; 66 if( lson[pos] ) { 67 int jl = judge(lson[pos],a,b); 68 if( jl == 4 ) ret += sum[lson[pos]]; 69 else if( jl ) ret += query(lson[pos],a,b); 70 } 71 if( rson[pos] ) { 72 int jr = judge(rson[pos],a,b); 73 if( jr == 4 ) ret += sum[rson[pos]]; 74 else if( jr ) ret += query(rson[pos],a,b); 75 } 76 return ret; 77 } 78 79 int main() { 80 static int n,m; 81 scanf("%d%d",&n,&m); 82 for(int i=1;i<=n;i++) 83 scanf("%lld%lld%lld",ps[i].d,ps[i].d+1,&ps[i].h); 84 85 build(cnt=1,1,n,0); 86 87 for(int i=1,a,b;i<=m;i++) { 88 scanf("%d%d%lld",&a,&b,&c); 89 printf("%lld ",query(1,a,b)); 90 } 91 return 0; 92 }
