搜索
DFS
void dfs(int x)
{
vis[x] = 1;
for(int i = head[x];i;i = e[i].x)
{
if(!vis[e[i].t])
{
dfs(e[i].t);
}
}
}
例1 P1101 单词方阵
题目描述
给一n×n的字母方阵,内可能蕴含多个“yizhong”单词。单词在方阵中是沿着同一方向连续摆放的。摆放可沿着 8个方向的任一方向,同一单词摆放时不再改变方向,单词与单词之间可以交叉,因此有可能共用字母。输出时,将不是单词的字母用*代替,以突出显示单词。例如:
输入:
8 输出:
qyizhong *yizhong
gydthkjy gy******
nwidghji n*i*****
orbzsfgz o**z****
hhgrhwth h***h***
zzzzzozo z****o**
iwdfrgng i*****n*
yyyygggg y******g
输入输出格式
输入格式:
第一行输入一个数n。(7≤n≤100)。
第二行开始输入n×n的字母矩阵。
输出格式:
突出显示单词的n×n矩阵。
输入输出样例
输入样例#1: 复制
7
aaaaaaa
aaaaaaa
aaaaaaa
aaaaaaa
aaaaaaa
aaaaaaa
aaaaaaa
输出样例#1: 复制
*******
*******
*******
*******
*******
*******
*******
输入样例#2: 复制
8
qyizhong
gydthkjy
nwidghji
orbzsfgz
hhgrhwth
zzzzzozo
iwdfrgng
yyyygggg
输出样例#2: 复制
*yizhong
gy******
n*i*****
o**z****
h***h***
z****o**
i*****n*
y******g
标程
#include<bits/stdc++.h>
using namespace std;
const int maxn=110;
char ss[maxn][maxn],zz[]="yizhong";
int vis[maxn][maxn];
int fuck[][2]={{-1,-1},{-1,0},{-1,1},{0,-1},{0,1},{1,-1},{1,0},{1,1}};
struct wahaha
{
int a,b;
}c[maxn];
void dfs_one(int n);
void dfs_tow(int x,int y,int k,int cnt,wahaha c[]);
void dfs_one(int n){
for(int i=0;i< n;++i){
for(int j=0;j< n;++j){
if(ss[i][j]=='y'){
for(int k = 0; k < 8; k++)
{
int x=i+fuck[k][0];
int y=j+fuck[k][1];
if(ss[x][y]=='i') {
dfs_tow(i,j,k,0,c);
}
}
}
}
}
}
void dfs_tow(int x,int y,int k,int cnt,wahaha c[]){
if(cnt==7) {
for(int i=0;i<7;++i){
vis[c[i].a][c[i].b]=1;
}
}
else{
int dx=x+fuck[k][0];
int dy=y+fuck[k][1];
if(cnt==6||ss[dx][dy]==zz[cnt+1]){
c[cnt].a=x;c[cnt].b=y;
dfs_tow(dx,dy,k,cnt+1,c);
}
}
}
inline void init()
{
int n;
scanf("%d",&n);
for(int i=0;i<n;++i){
scanf("%s",&ss[i]);
}
memset(vis,0,sizeof(vis));
dfs_one(n);
for(int i=0;i<n;++i){
for(int j=0;j<n;++j){
if(vis[i][j]) printf("%c",ss[i][j]);
else printf("*");
}
printf("
");
}
}
int main(int argc, char const *argv[])
{
init();
return 0;
}
例2 P1605 迷宫
题目背景
给定一个N*M方格的迷宫,迷宫里有T处障碍,障碍处不可通过。给定起点坐标和
终点坐标,问: 每个方格最多经过1次,有多少种从起点坐标到终点坐标的方案。在迷宫
中移动有上下左右四种方式,每次只能移动一个方格。数据保证起点上没有障碍。
1≤N,M≤5
输入输出格式
输入格式:
【输入】
第一行N、M和T,N为行,M为列,T为障碍总数。第二行起点坐标SX,SY,终点
坐标FX,FY。接下来T行,每行为障碍点的坐标。
输出格式:
【输出】
给定起点坐标和终点坐标,问每个方格最多经过1次,从起点坐标到终点坐标的方
案总数。
输入输出样例
输入样例#1: 复制
2 2 1
1 1 2 2
1 2
输出样例#1: 复制
1
标程
#include<bits/stdc++.h>
using namespace std;
int SX,SY,FX,FY;
int MAP[6][6],vis[6][6];
int dx[]={0,0,-1,1},dy[]={-1,1,0,0};
int ans=0;
int n,m,t;
void dfs(int x,int y)
{
if(x==FX && y==FY)
{
ans++;
return ;
}
else
{
for(int i = 0; i <= 3; i++)
{
if(vis[x+dx[i]][y+dy[i]]==0 && MAP[x+dx[i]][y+dy[i]]==1)
{
vis[x][y]=1;
dfs(x+dx[i],y+dy[i]);
vis[x][y]=0;
}
}
}
}
inline void init()
{
scanf("%d%d%d",&n,&m,&t);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
MAP[i][j]=1;
}
}
scanf("%d%d%d%d",&SX,&SY,&FX,&FY);
for(int i=1;i<=t;++i)
{
int x,y;
scanf("%d%d",&x,&y);
MAP[x][y]=0;
}
memset(vis,0,sizeof(vis));
dfs(SX,SY);
printf("%d",ans);
}
int main(int argc, char const *argv[])
{
init();
return 0;
}
例3 P1019 单词接龙
题目描述
单词接龙是一个与我们经常玩的成语接龙相类似的游戏,现在我们已知一组单词,且给定一个开头的字母,要求出以这个字母开头的最长的“龙”(每个单词都最多在“龙”中出现两次),在两个单词相连时,其重合部分合为一部分,例如 beastbeast和astonish,如果接成一条龙则变为beastonish,另外相邻的两部分不能存在包含关系,例如at 和 atide 间不能相连。
输入输出格式
输入格式:
输入的第一行为一个单独的整数n (n≤20)表示单词数,以下n 行每行有一个单词,输入的最后一行为一个单个字符,表示“龙”开头的字母。你可以假定以此字母开头的“龙”一定存在.
输出格式:
只需输出以此字母开头的最长的“龙”的长度
输入输出样例
输入样例#1: 复制
5
at
touch
cheat
choose
tact
a
输出样例#1: 复制
23
说明
(连成的“龙”为atoucheatactactouchoose)
NOIp2000提高组第三题
标程
#include<bits/stdc++.h>
using namespace std;
const int maxn=105;
char a[55][55],b[55];
int n,np=0,first[maxn],ans=100000,vis[maxn];
struct edge{
int to,next,w;
}E[maxn<<1];
void addedge(int u,int v,int w)
{
E[++np]=(edge){v,first[u],w};
first[u]=np;
// printf("%d %d %d
",u,v,w);
}
void dfs(int i,int l)
{
vis[i]++;//技巧
ans=max(ans,l);
for(int p=first[i];p;p=E[p].next)
{
int j=E[p].to,w=E[p].w;
if(vis[j]==2) continue;
dfs(j,l+w);
}
vis[i]--;
}
int check(int i,int j)
{
int lenj=strlen(a[j]);
int leni=strlen(a[i]);
int ans=0;
int k;
for(k=0;k+1<min(leni,lenj);k++)
{
int ok=1;
for(int r=0;r<=k;r++)
{
if(a[i][leni-1-k+r]!=a[j][r]) {ok=0;break;}
}
if(ok){ ans=k+1;break;}
}
if(ans==0) return 0;
return lenj-ans;
}
void init()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%s",&a[i]);memcpy(a[i+n],a[i],sizeof(a[i]));
}
scanf("%s",a[2*n+1]);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
int w=check(i,j);
if(w) addedge(i,j,w);
}
for(int i=1;i<=n;i++)//最后一个点编号随意
{
if(a[i][0]==a[2*n+1][0]) addedge(2*n+1,i,strlen(a[i])-1);
}
}
int main()
{
init();
ans=0;
dfs(2*n+1,1);
printf("%d",ans);
return 0;
}
例4 P1162 马的遍历
题目描述
由数字0组成的方阵中,有一任意形状闭合圈,闭合圈由数字1构成,围圈时只走上下左右4个方向。现要求把闭合圈内的所有空间都填写成2.例如:6×6的方阵(n=6),涂色前和涂色后的方阵如下:
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1
输入输出格式
输入格式:
每组测试数据第一行一个整数n(1≤n≤30)
接下来n行,由0和1组成的n×n的方阵。
方阵内只有一个闭合圈,圈内至少有一个0。
//感谢黄小U饮品指出本题数据和数据格式不一样. 已修改(输入格式)
输出格式:
已经填好数字2的完整方阵。
输入输出样例
输入样例#1: 复制
6
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1
输出样例#1: 复制
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1
标程
#include<bits/stdc++.h>
using namespace std;
int maps[100][100],mapCLON[100][100]={0};
int n,x,y;
void dfs(int x,int y)
{
if(x>n||x<1||y>n||y<1||maps[x][y]!=0)//判断是否越界
return;
maps[x][y]=1;
dfs(x+1,y);
dfs(x-1,y);
dfs(x,y+1);
dfs(x,y-1);//四个方向
}
inline void init()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
cin>>maps[i][j];
if(maps[i][j]==1) mapCLON[i][j]=-1;//b用来存原来的位置
}
int flag=0;
for(int i=1;i<=n;i++)
{
if(maps[i][1]!=1) dfs(i,1);
if(maps[i][n]!=1) dfs(i,n);//搜第i行的第一列和第n列
}
for(int i=1;i<=n;i++)
{
if(maps[1][i]!=1) dfs(1,i);
if(maps[n][i]!=1) dfs(n,i);//搜第i列的第一行和第n行
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(mapCLON[i][j]==-1) printf("1 ");
else if(maps[i][j]==0) printf("2 ");
else printf("0 ");
}
printf("
");
}
}
int main()
{
init();
return 0;
}
剪枝优化
例1 P1433 吃奶酪
题目描述
房间里放着n块奶酪。一只小老鼠要把它们都吃掉,问至少要跑多少距离?老鼠一开始在(0,0)点处。
输入输出格式
输入格式:
第一行一个数n (n<=15)
接下来每行2个实数,表示第i块奶酪的坐标。
两点之间的距离公式=sqrt((x1-x2)(x1-x2)+(y1-y2)(y1-y2))
输出格式:
一个数,表示要跑的最少距离,保留2位小数。
输入输出样例
输入样例#1: 复制
4
1 1
1 -1
-1 1
-1 -1
输出样例#1: 复制
7.41
标程
#include<bits/stdc++.h>
using namespace std;
int n,vis[1001];
double x[100],y[20];
double dis[1001][1001];
double ans=0x3f3f3f;
inline void init()
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>x[i]>>y[i];
x[0]=0;y[0]=0;
for(int i=0;i<=n;i++)
for(int j=0;j<=n;j++)
dis[i][j]=sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));
}
void dfs(int step,int now,double length)
{
if(length>ans)
return;
if(step==n)
{
ans=min(ans,length);
return;
}
for(int i=1;i<=n;i++)
if(!vis[i])
{
vis[i]=1;
dfs(step+1,i,length+dis[now][i]);
vis[i]=0;
}
}
int main(void)
{
init();
dfs(0,0,0.0);
printf("%.2f",ans);
return 0;
}
例2 P1312 MaYan游戏
题目描述
Mayan puzzle是最近流行起来的一个游戏。游戏界面是一个7 行5×5列的棋盘,上面堆放着一些方块,方块不能悬空堆放,即方块必须放在最下面一行,或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块,消除方块的规则如下:
1 、每步移动可以且仅可以沿横向(即向左或向右)拖动某一方块一格:当拖动这一方块时,如果拖动后到达的位置(以下称目标位置)也有方块,那么这两个方块将交换位置(参见输入输出样例说明中的图6到图7 );如果目标位置上没有方块,那么被拖动的方块将从原来的竖列中抽出,并从目标位置上掉落(直到不悬空,参见下面图1 和图2);
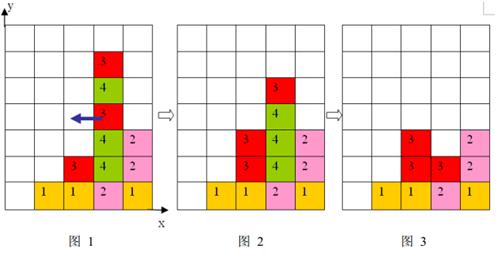
2 、任一时刻,如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块,则它们将立即被消除(参见图1 到图3)。
注意:
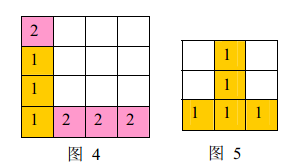
a) 如果同时有多组方块满足消除条件,几组方块会同时被消除(例如下面图4 ,三个颜色为1 的方块和三个颜色为 2 的方块会同时被消除,最后剩下一个颜色为2的方块)。
b) 当出现行和列都满足消除条件且行列共享某个方块时,行和列上满足消除条件的所有方块会被同时消除(例如下面图5 所示的情形,5 个方块会同时被消除)。
3 、方块消除之后,消除位置之上的方块将掉落,掉落后可能会引起新的方块消除。注意:掉落的过程中将不会有方块的消除。
上面图1 到图 3 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为(0, 0 ),将位于(3, 3 )的方块向左移动之后,游戏界面从图 1 变成图 2 所示的状态,此时在一竖列上有连续三块颜色为4 的方块,满足消除条件,消除连续3 块颜色为4 的方块后,上方的颜色为3 的方块掉落,形成图 3 所示的局面。
输入输出格式
输入格式:
共 6 行。
第一行为一个正整数n,表示要求游戏通关的步数。
接下来的5行,描述7×5 的游戏界面。每行若干个整数,每两个整数之间用一个空格隔开,每行以一个0 结束,自下向上表示每竖列方块的颜色编号(颜色不多于10种,从1开始顺序编号,相同数字表示相同颜色)。
输入数据保证初始棋盘中没有可以消除的方块。
输出格式:
如果有解决方案,输出n行,每行包含 3 个整数x,y,g表示一次移动,每两个整数之间用一个空格隔开,其中(x,y)表示要移动的方块的坐标,g 表示移动的方向,1 表示向右移动,−1表示向左移动。注意:多组解时,按照x为第一关健字,y为第二关健字,1优先于−1 ,给出一组字典序最小的解。游戏界面左下角的坐标为(0,0)。
如果没有解决方案,输出一行,包含一个整数−1。
输入输出样例
输入样例#1: 复制
3
1 0
2 1 0
2 3 4 0
3 1 0
2 4 3 4 0
输出样例#1: 复制
2 1 1
3 1 1
3 0 1
说明
【输入输出样例说明】
按箭头方向的顺序分别为图6到图11
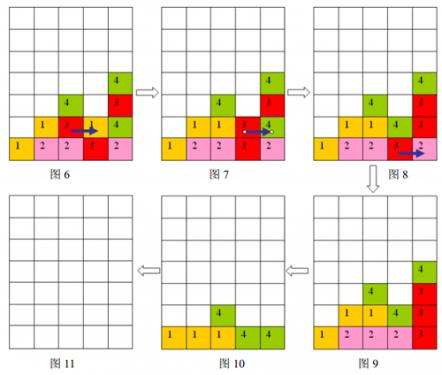
样例输入的游戏局面如上面第一个图片所示,依次移动的三步是:(2,1)处的方格向右移动,(3,1)处的方格向右移动,(3,0)(3,0)处的方格向右移动,最后可以将棋盘上所有方块消除。
【数据范围】
对于30%的数据,初始棋盘上的方块都在棋盘的最下面一行;
对于100%的数据,0<n≤5 。
noip2011提高组day1第3题
标程
#include <bits/stdc++.h>
using namespace std;
#define il inline
int n;
int mapp[10][10],ans[10][10],last[10][10][10],tong[10][10];
il int read()
{
int X=0,w=0; char ch=0;
while(!isdigit(ch)) {w|=ch=='-';ch=getchar();}
while(isdigit(ch)) X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
return w?-X:X;
}
il bool reover()
{
bool flag = 1;
for(int i = 1;i <= 5;++i)
for(int j = 1;j <= 7;++j)
{
if(i-1 >= 1 && i+1 <= 5 && mapp[i][j] && mapp[i][j] == mapp[i-1][j] && mapp[i][j] == mapp[i+1][j])
{
tong[i][j] = 1;
tong[i-1][j] = 1;
tong[i+1][j] = 1;
flag = 0;
}
if(j-1 >= 1 && j+1 <= 7 && mapp[i][j] && mapp[i][j] == mapp[i][j-1] && mapp[i][j] == mapp[i][j+1])
{
tong[i][j] = 1;
tong[i][j-1] = 1;
tong[i][j+1] = 1;
flag = 0;
}
}
if(flag) return 0;
for(int i = 1;i <= 5;++i)
for(int j = 1;j <= 7;++j)
{
if(tong[i][j])
{
mapp[i][j] = 0;
tong[i][j] = 0;
}
}
return 1;
}
//玩完了
il bool gameover()
{
for(int i = 1;i <= 5;++i)
if(mapp[i][1]) return 0;
return 1;
}
//记录操作(搜索回溯还原)
il void copy (int x)
{
for(int i = 1;i <= 5;++i)
for(int j = 1;j <= 7;++j)
{
last[x][i][j] = mapp[i][j];
}
}
//下沉操作
il void update()
{
for(int i = 1;i <= 5;++i)
{
int flag = 0;
for(int j = 1;j <= 7;++j)
{
if(!mapp[i][j]) flag++;
else
{
if(!flag) continue;
mapp[i][j - flag] = mapp[i][j];
mapp[i][j] = 0;
}
}
}
}
//交换操作
il void move(int i,int j,int flag)
{
swap(mapp[i][j],mapp[i+flag][j]);
update();
while(reover()) update();
}
//搜索
void dfs(int x)
{
if(gameover())
{
for(int i = 1;i <= n;++i)
{
if(i != 1) cout << endl;
cout << ans[i][1] <<" "<< ans[i][2] <<" "<< ans[i][3];
}
exit(0);
}
if(x == n+1) return;
copy(x);
for(int i = 1;i <= 5;++i)
for(int j = 1;j <= 7;++j)
{
if(mapp[i][j])
{
if(i-1 >= 1 && mapp[i-1][j] == 0)
{
move(i,j,-1);
ans[x][1] = i-1;
ans[x][2] = j-1;
ans[x][3] = -1;
dfs(x+1);
for(int i = 1;i <= 5;++i)
for(int j = 1;j <= 7;++j)
mapp[i][j] = last[x][i][j];
ans[x][1] = 0;
ans[x][2] = 0;
ans[x][3] = 0;
}
if(i+1 <= 5 && mapp[i][j] != mapp[i+1][j])
{
move(i,j,1);
ans[x][1] = i-1;
ans[x][2] = j-1;
ans[x][3] = 1;
dfs(x+1);
for(int i = 1;i <= 5;++i)
for(int j = 1;j <= 7;++j)
mapp[i][j] = last[x][i][j];
ans[x][1] = 0;
ans[x][2] = 0;
ans[x][3] = 0;
}
}
}
}
int main(int argc, char const *argv[])
{
n = read();
for(int i = 1;i <= 5;++i)
for(int j = 1;j <= 8;++j)
{
int x = read();
if(x == 0) break;
mapp[i][j] = x;
}
dfs(1);
printf("-1
");
return 0;
}
例3 P1120 小木棍
题目描述
乔治有一些同样长的小木棍,他把这些木棍随意砍成几段,直到每段的长都不超过50。
现在,他想把小木棍拼接成原来的样子,但是却忘记了自己开始时有多少根木棍和它们的长度。
给出每段小木棍的长度,编程帮他找出原始木棍的最小可能长度。
输入输出格式
输入格式:
共二行。
第一行为一个单独的整数N表示砍过以后的小木棍的总数,其中N≤65
(管理员注:要把超过50的长度自觉过滤掉,坑了很多人了!)
第二行为N个用空个隔开的正整数,表示N根小木棍的长度。
输出格式:
一个数,表示要求的原始木棍的最小可能长度
输入输出样例
输入样例#1: 复制
9
5 2 1 5 2 1 5 2 1
输出样例#1: 复制
6
说明
2017/08/05
数据时限修改:
-#17 #20 #22 #27 四组数据时限500ms
-#21 #24 #28 #29 #30五组数据时限1000ms
其他时限改为200ms(请放心食用)
标程
#include<bits/stdc++.h>
using namespace std;
const int maxx = 66;
int n,maxn = -maxx,minn = maxx;
int tong[maxx];
void dfs( int res , int sum , int target , int p ) {
if( res == 0 ) {
printf("%d", target );
exit( 0 );
}
if( sum == target ) {
dfs( res - 1 , 0 , target , maxn );
return;
}
for( int i = p ; i >= minn ; i -- ) {
if( tong[ i ] && i + sum <= target ) {
tong[ i ] -- ;
dfs( res , sum + i , target , i );
tong[ i ] ++ ;
if ( sum == 0 || sum + i == target )
break;
}
}
return;
}
int main(int argc, char const *argv[])
{
scanf("%d",&n);
int x,cnt = 0,sum;
while(n--)
{
scanf("%d",&x);
if(x <= 50)
{
cnt++;
tong[x]++;
sum += x;
maxn = max(maxn,x);
minn = min(minn,x);
}
}
x = sum/2;
for(int i = maxn;i <= x;i++)
{
if(sum%i == 0)
{
dfs(sum/i,0,i,maxn);
}
}
printf("%d",sum);
return 0;
}