数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已。

5.1、数据清洗
5.1.1 数据样本抽样
· 样本要具有代表性
· 样本比例要平衡以及样本不均衡时如何处理
· 考虑全量数据
5.1.2异常值(空值)处理
· 识别异常值和重复值
Pandas:isnull()/duplicated()----判断是否有重复的项
·
直接丢弃(包括重复数据)
Pandas:drop()/dropna()/drop_duplicated()
·
把异常当作一个新的属性,替代原值
Pandas:fillna()
·
集中值指代
Pandas:fillna()
·
边界值指代
Pandas:fillna()
·
插值
Pandas:interpolate() --- 针对于Series
若插入值是位于首部,则插入第二个数的数值大小;
若插入值是位于尾部,则插入倒数第二个数的数值大小;
若插入值位于中部,则取前后两数的平均值;
import numpy as np
import pandas as pd
df = pd.DataFrame({'A':['a0','a1','a1','a2','a3','a4'],
'B':['b0','b1','b2','b2','b3',None],
'C':[1,2,None,3,4,5],
'D':[0.1,10.2,11.4,8.9,9.1,12],
'E':[10,19,32,25,8,None],
'F':['f0','f1','g2','f3','f4','f5']})
print(df)
# print(df.duplicated())
#删除空值所在行
# df = df.dropna()
#删除某一属性的空值
df = df.dropna(subset=['B'])
#删除重复数所在的行,保留第一个(默认),last为保留最后一个
df = df.drop_duplicates('A',keep='first')
df['B'] = df.fillna('b*')
#插值只能对Series进行处理
df['E'] = df['E'].interpolate()
upper_q = df['D'].quantile(q=0.75)
lower_q = df['D'].quantile(q=0.25)
k = 1.5
q_int = upper_q - lower_q
df = df[df['D'] < upper_q + k * q_int][df["D"] > lower_q - k * q_int]
# print(pd.Series([1,None,9,16,25]).interpolate())
print(df)
#要求F列必须以f开头
df[[True if item.startswith('f') else False for item in list(df['F'].values)]]
print(df)
'''
结果:
A B C D E F
1 a1 a1 2.0 10.2 19.0 f1
3 a2 a2 3.0 8.9 25.0 f3
4 a3 a3 4.0 9.1 8.0 f4
'''
5.2、特征预处理
标注(标记、标签label)-------反应目的的属性
5.2.1特征选择
剔除与标注不相关或者冗余的属性
思路:过滤思想(SelectKBest:是对卡方检验的实现---检验定性自变量对定性因变量的相关性)
卡方检验就是统计样本的实际观测值与理论值推断之间的偏离程度,卡方值越大,越不符合!
包裹思想(RFE)、
嵌入思想(SelectModel)

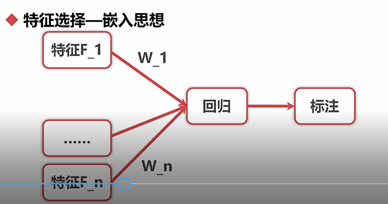
import numpy as np
import pandas as pd
import scipy.stats as ss
df = pd.DataFrame({'A':ss.norm.rvs(size =10),
'B':ss.norm.rvs(size =10),
'C':ss.norm.rvs(size=10),
'D':np.random.randint(low=0,high=2,size=10)})
print('原始数据','
',df)
from sklearn.svm import SVR
from sklearn.tree import DecisionTreeRegressor
#特征
X = df.loc[:,['A','B','C']]
#标注
Y = df.loc[:,'D']
#引入特征选择的主要方法
# SelectKBest是过滤思想常用的一个类,RFE是包裹思想常用的类,SelectModel是嵌入思想常用的类
from sklearn.feature_selection import SelectKBest,RFE,SelectFromModel
#过滤思想
#k表示特征选择的自由度
skb = SelectKBest(k=2)
skb.fit(X,Y)
skbTran = skb.transform(X)
print('过滤思想过滤后的值','
',skbTran)
#包裹思想
#n_features_to_select只最终要选择的特征个数;
# step表示没迭代一次需要去掉的特征数
rfe = RFE(estimator = SVR(kernel='linear'),n_features_to_select=2,step=1)
# rfe.fit(X,Y)
# rfeTran = rfe.transform(X)
rfeTran = rfe.fit_transform(X,Y)
print('包裹思想过滤后的值','
',rfeTran)
#嵌入思想
#threshold笔试中重要因子的数,低于这个值将会被去掉
sfm = SelectFromModel(estimator=DecisionTreeRegressor(),threshold=0.001)
sfmTran = sfm.fit_transform(X,Y)
print('嵌入思想过滤后的值','
',sfmTran)
'''
原始数据
A B C D
0 -0.343069 1.209042 0.907560 1
1 -1.639497 0.079508 -0.906982 0
2 -0.469982 1.218025 -1.683698 1
3 1.985778 0.623312 -0.362048 0
4 -0.702992 0.225288 -0.093547 0
5 -0.758332 0.888060 0.873699 0
6 -0.448316 -1.424388 1.156535 1
7 0.278143 -0.137433 0.235821 1
8 -0.609878 0.971602 -1.385594 0
9 0.695930 1.942863 -0.933565 0
过滤思想过滤后的值
[[ 1.20904233 0.90756004]
[ 0.07950784 -0.90698164]
[ 1.21802486 -1.68369767]
[ 0.62331202 -0.36204764]
[ 0.22528754 -0.0935473 ]
[ 0.88805974 0.87369887]
[-1.4243878 1.15653461]
[-0.13743341 0.23582091]
[ 0.97160152 -1.38559355]
[ 1.94286318 -0.9335654 ]]
包裹思想过滤后的值
[[ 1.20904233 0.90756004]
[ 0.07950784 -0.90698164]
[ 1.21802486 -1.68369767]
[ 0.62331202 -0.36204764]
[ 0.22528754 -0.0935473 ]
[ 0.88805974 0.87369887]
[-1.4243878 1.15653461]
[-0.13743341 0.23582091]
[ 0.97160152 -1.38559355]
[ 1.94286318 -0.9335654 ]]
嵌入思想过滤后的值
[[-0.34306925]
[-1.63949715]
[-0.46998151]
[ 1.98577754]
[-0.70299218]
[-0.75833209]
[-0.44831583]
[ 0.27814316]
[-0.60987799]
[ 0.69592956]]
'''
5.2.2 特征变换
方法:
(1)对指化(numpy.log(),numpy.exp())
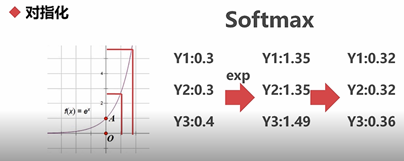
sum_exp = sum([1.35,1.35,1.49]) softmax = [round(i/sum_exp,3) for i in [1.35,1.35,1.49]] print(softmax) #[0.322, 0.322, 0.356]
(2)离散化(数据平滑):将连续变量分成几段(bins)
原因:克服数据缺陷、默写算法要求(例:朴素贝叶斯)、非线性数据映射。
方法:等频(等深分箱qcut())、等距(等宽分箱cut())、自因变量优化(即根据自变量、因变量的分布找到特殊拐点进行离散化,可见探索性数据分析4.2.3相关分析)
数据进行分箱之前必须排序
import numpy as np import pandas as pd lst = [6,8,10,15,16,24,25,40,67] #等深分箱 print(pd.qcut(lst,q=3)) print(pd.qcut(lst,q=3,labels=['low','medium','high'])) #等宽分箱 print(pd.cut(lst,bins=3)) print(pd.cut(lst,bins=3,labels=['low','medium','high']))
(3)归一化(MinMaxScaler()):将数据的范围先定在0,1之间
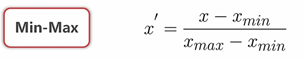
(4)标准化、正态化(StandardScaler() 此处所指标准化是狭义上的标准化,指的是将数据缩放到均值为0,标准差为1的尺度上,从而体现一个数据与该特征下其他数据的相对大小的关系)
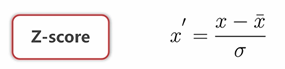
import numpy as np
import pandas as pd
#preprocessing庫中包括许多的预处理函数
from sklearn.preprocessing import MinMaxScaler,StandardScaler
#归一化
#reshape(-1,1)表示不指定具体的行数,但必须是1列
guiyi = MinMaxScaler().fit_transform(np.array([1,4,9,16,25]).reshape(-1,1))
print('归一化结果','
',guiyi.reshape(1,-1))
#标准化
stand = StandardScaler().fit_transform(np.array([1,4,9,16,25]).reshape(-1,1))
print('标准化结果','
',stand.reshape(1,-1))
'''
归一化结果
[[0. 0.125 0.33333333 0.625 1. ]]
标准化结果
[[-1.15624323 -0.80937026 -0.23124865 0.57812161 1.61874052]]
'''
(5)数值化:将非数值数据转化成数值数据的过程

定类:标签化(LabelEncoder)
定序:独热(OneHotEncoder)


import numpy as np
import pandas as pd
from sklearn.preprocessing import LabelEncoder,OneHotEncoder
#标签化
label = LabelEncoder().fit_transform(["Down","Up","Up","Down"])
print('标签化结果:','
',label) #[0 1 1 0]
#读热编码
label_encoder = LabelEncoder()
label_trans = label_encoder.fit_transform(np.array(["Red","Yellow","Blue","Green"]))
print('标签化后结果:','
',label_trans) #[2 3 0 1]----按照首字母的顺序
oht_encoder = OneHotEncoder().fit(label_trans.reshape(-1,1))
oneHot_trans = oht_encoder.transform(label_encoder.transform(np.array(["Red","Blue","Green"])).reshape(-1,1)).toarray()
print('读热结果:','
',oneHot_trans)
# [[0. 0. 1. 0.]
# [1. 0. 0. 0.]
# [0. 1. 0. 0.]]
注意:pandas库中提供的直接进行OneHotEncoder()的方法是get_dummies()
df = pd.get_dummies(df,columns= ['department'])
(6)正规化(规范化Normalizer()):将一个向量的长度正规到单位1


在数据分析处理中的正规化的三种用法:
a:用在特征上(使用的较少)
b:用在每个对象的各个特征的表示(特征矩阵的行)
c:模型的参数上(回归模型使用较多)
import numpy as np
import pandas as pd
from sklearn.preprocessing import Normalizer
norm1 = Normalizer(norm = 'l1').fit_transform(np.array([1,1,3,-1,2]).reshape(-1,1))
#正规化实际上是对行进行正规化
print('正规化的结果:','
',norm1)
norm2 = Normalizer(norm = 'l1').fit_transform(np.array([[1,1,3,-1,2]]))
print('正规化的结果(对行进行处理):','
',norm2)# [[ 0.125 0.125 0.375 -0.125 0.25 ]]
norm3 = Normalizer(norm = 'l2').fit_transform(np.array([[1,1,3,-1,2]]))
print('正规化的结果(对行进行处理):','
',norm3)# [[ 0.25 0.25 0.75 -0.25 0.5 ]]
5.2.3 特征降维
(1)PCA、奇异值分解等线性降维
· 求特征协方差矩阵
· 求协方差的特征值和特征向量
· 将特征值从大到小排序,选择其中最大的k个
· 将样本点投影到选取的特征向量上
(2)LDA降维(Linear Discriminant Analysis 线性判别式分析)
核心思想:投影变化后同一标注内距离尽可能小;不同标注间距离尽可能大
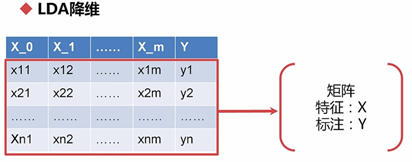


乘以参数矩阵w0和w1时,标注Y并不参与其中
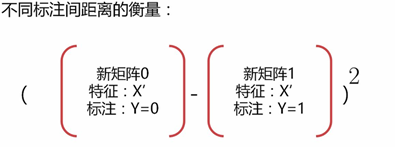


转化成数学公式:

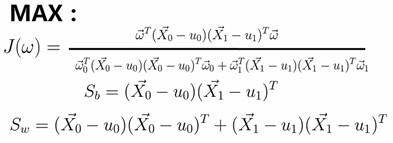
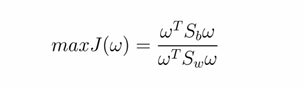
import numpy as np
import pandas as pd
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
X = np.array([[-1,-1],[-2,-1],[-3,-2],[1,1],[2,1],[3,2]])
Y = np.array([1,1,1,2,2,2])
#n_components=1表示将至1维
lda = LinearDiscriminantAnalysis(n_components=1).fit_transform(X,Y)
print('LDA降维后的效果:','
',lda)
'''
LDA降维后的效果:
[[-1.73205081]
[-1.73205081]
[-3.46410162]
[ 1.73205081]
[ 1.73205081]
[ 3.46410162]]
'''
#也可以将LDA作为一个分类器
clf = LinearDiscriminantAnalysis(n_components=1).fit(X,Y)
predict = clf.predict([[0.8,2],[-5,4]])
print('预测结果:',predict) #预测结果: [2 2]
5.2.4 特征衍生
加减乘除
求导与高阶求导
人工归纳

5.2.5 实例:HR表的特征处理
import numpy as np
import pandas as pd
from sklearn.preprocessing import MinMaxScaler,StandardScaler,LabelEncoder,OneHotEncoder,Normalizer
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.decomposition import PCA
pd.set_option('display.max_columns',None) #控制列的输出
#sl:satisfaction_level ---- False:MinMaxScaler;True:StandardScaler
#le:last_evaluation ---- False:MinMaxScaler;True:StandardScaler
#npr:number_project ---- False:MinMaxScaler;True:StandardScaler
#amh:average_monthly_hours ---- False:MinMaxScaler;True:StandardScaler
#tsc:time_spend_company ---- False:MinMaxScaler;True:StandardScaler
#wa:Work_accident ---- False:MinMaxScaler;True:StandardScaler
#pl5:promotion_last_5years ---- False:MinMaxScaler;True:StandardScaler
#dp:department ---- False:LabelEncoder;True:OneHotEncoder
#slr:salary ---- False:LabelEncoder;True:OneHotEncoder
def hr_preprocessing(sl = False,le = False,npr = False,amh = False,tsc = False,
wa = False,pl5 = False,dp = False,slr = False,lower_d = False,ld_n = 1):
df = pd.read_csv('yuanHR.csv')
# 1、清洗数据--即去除异常值或抽样
df = df.dropna(subset=['satisfaction_level','last_evaluation'])
df = df[df['satisfaction_level']<=1][df['salary']!='nme']
# 2、得到标注
label = df['left']
df = df.drop('left', axis=1)
#3、特征选择
#4、特征处理
scaler_lst = [sl,le,npr,amh,tsc,wa,pl5]
column_lst = ['satisfaction_level','last_evaluation','number_project',
'average_monthly_hours','time_spend_company','Work_accident',
'promotion_last_5years']
for i in range(len(scaler_lst)):
if not scaler_lst[i]:
df[column_lst[i]] =
MinMaxScaler().fit_transform(df[column_lst[i]].values.reshape(-1,1)).reshape(1,-1)[0]
else:
df[column_lst[i]] =
StandardScaler().fit_transform(df[column_lst[i]].values.reshape(-1,1)).reshape(1,-1)[0]
scaler_lst = [slr, dp]
column_lst = ['salary', 'department']
for i in range(len(scaler_lst)):
if not scaler_lst[i]:
if column_lst[i] == 'salary':
df[column_lst[i]] = [map_salary(s) for s in df['salary'].values]
else:
df[column_lst[i]] = LabelEncoder().fit_transform(df[column_lst[i]])
#將'salary', 'department'进行归一化处理
df[column_lst[i]] = MinMaxScaler().fit_transform(df[column_lst[i]].values.reshape(-1,1)).reshape(1,-1)[0]
else:
#pandas库中提供的直接进行OneHotEncoder的方法是get_dummies()
df = pd.get_dummies(df,columns=[column_lst[i]])
if lower_d == True:
return PCA(n_components=ld_n).fit_transform(df.values)
return df,label
d =dict([("low",0),('medium',1),('high',2)])
def map_salary(s):
return d.get(s,0)
def main():
print(hr_preprocessing())
if __name__ == "__main__":
main()