Terrible Sets
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 5325 | Accepted: 2713 |
Description
Let N be the set of all natural numbers {0 , 1 , 2 , . . . }, and R be the set of all real numbers. wi, hi for i = 1 . . . n are some elements in N, and w0 = 0.
Define set B = {< x, y > | x, y ∈ R and there exists an index i > 0 such that 0 <= y <= hi ,∑0<=j<=i-1wj <= x <= ∑0<=j<=iwj}
Again, define set S = {A| A = WH for some W , H ∈ R+ and there exists x0, y0 in N such that the set T = { < x , y > | x, y ∈ R and x0 <= x <= x0 +W and y0 <= y <= y0 + H} is contained in set B}.
Your mission now. What is Max(S)?
Wow, it looks like a terrible problem. Problems that appear to be terrible are sometimes actually easy.
But for this one, believe me, it's difficult.
Define set B = {< x, y > | x, y ∈ R and there exists an index i > 0 such that 0 <= y <= hi ,∑0<=j<=i-1wj <= x <= ∑0<=j<=iwj}
Again, define set S = {A| A = WH for some W , H ∈ R+ and there exists x0, y0 in N such that the set T = { < x , y > | x, y ∈ R and x0 <= x <= x0 +W and y0 <= y <= y0 + H} is contained in set B}.
Your mission now. What is Max(S)?
Wow, it looks like a terrible problem. Problems that appear to be terrible are sometimes actually easy.
But for this one, believe me, it's difficult.
Input
The input consists of several test cases. For each case, n is given in a single line, and then followed by n lines, each containing wi and hi separated by a single space. The last line of the input is an single integer -1, indicating the end of input. You may assume that 1 <= n <= 50000 and w1h1+w2h2+...+wnhn < 109.
Output
Simply output Max(S) in a single line for each case.
Sample Input
3 1 2 3 4 1 2 3 3 4 1 2 3 4 -1
Sample Output
12 14
题意:
在 x 轴上给定一些不会重叠的矩形宽和高,矩形沿着x轴对齐,求这些矩形组成的连续矩形区域的最大面积。
Sample One
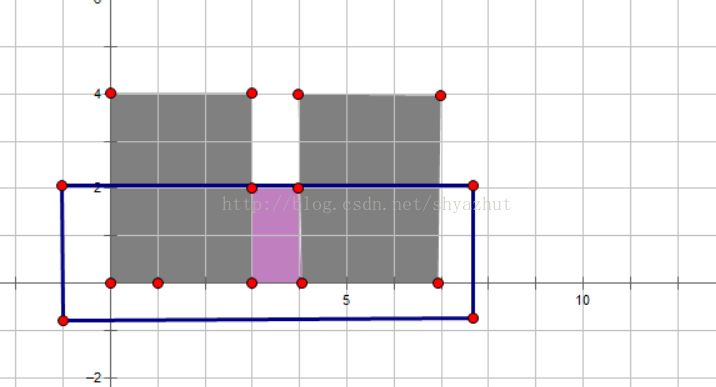
题解:维护一个高度非递减的栈,如果遇到一个高度更小的矩形,则他和比他高的矩形可共用底边,而当他入队时,他的宽就是和前面可共用的宽的和,(而后面的进来的矩形一定比他高更大,所以无影响,而比他低的又可以和他共用底)注意一边弹栈一边更新ans的值
#include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> #include<stack> using namespace std; const int maxn = 50000 + 5; struct node{ int h,w; }p[maxn]; int H[maxn]; int main(){ int n; ios::sync_with_stdio(false); while(scanf("%d",&n)==1){ if(n == -1)break; int ans = 0; stack <node> s; for(int i = 1; i <= n; i++){ cin>>p[i].w>>p[i].h; int nw = 0, nh =0; if(!s.empty() && p[i].h < s.top().h){ while(!s.empty() && p[i].h < s.top().h){ nw += s.top().w; nh = s.top().h; ans = max(ans , nw*nh); s.pop(); } p[i].w += nw; s.push(p[i]); } else s.push(p[i]); } int nw = 0, nh = 0; while(!s.empty()){ nh = s.top().h; nw += s.top().w; ans = max(ans , nw*nh); s.pop(); } cout<<ans<<endl; } }