这一章节其实就是讲一个主题——判断模型有无高方差或高偏差,也就是过拟合还是欠拟合。同时,如果模型有问题,怎么修正这一问题?
需要注意的是,这一章主要针对线性回归问题。当然,这一思路也可以应用于逻辑回归和简单的神经网络的训练。
个人是按照按照作业里设置好的训练步骤,逐条记录,和课程的顺序有所不同。
数据集的划分

NG的建议是,将总数据集划分为60%的Train set,20%的Cross validation set和20%的Test set。这里解释下各集合的作用:
- Train set:训练集。顾名思义,专门用作训练。
- Cross validation set:交叉验证集。是用来辅助训练,判断训练集的拟合情况,绘制学习曲线的。
- Test set:检验集。用来检验训练模型的准确度。
学习曲线
不同情况的特点
这里介绍的是如何通过学习曲线来判断模型的问题。这里有三种学习曲线:

这是高偏差情况。学习曲线的特点是交叉集和训练集曲线趋于收敛,但是收敛值偏高(区分好交叉验证集、训练集和试验集的不同)。对于高偏差情况,一味地增加数据量是没用的。
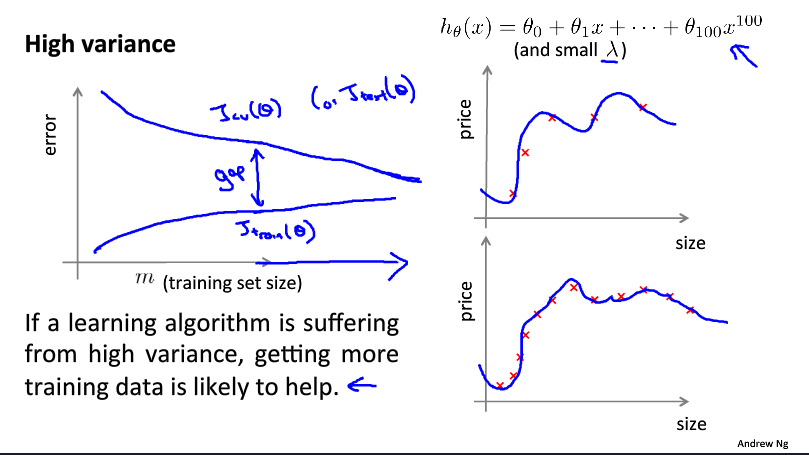
这是高方差情况。学习曲线的特点是两条曲线很难收敛。对于高方差情况(也就是过拟合),增加数据量是有效的。
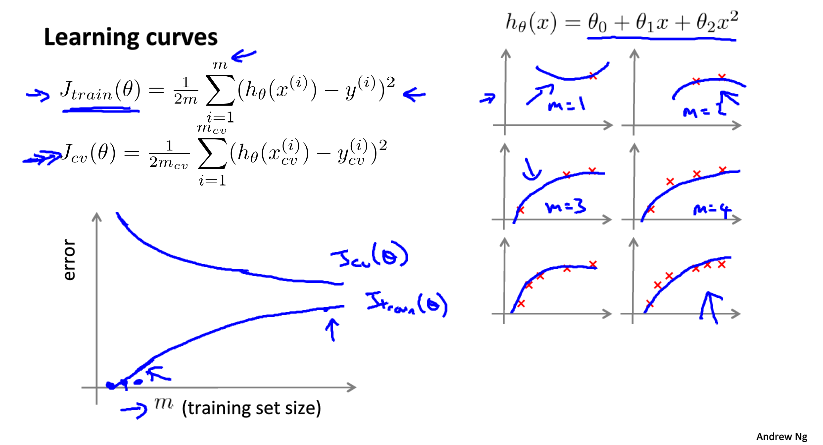
这是正确的学习曲线,当然只是理论上的。学习曲线的特点是趋于收敛,且收敛值很低。这里增加数据量也是很有效的。
以作业作为实例
需要注意的是,上面只是理论上的情况。实际上学习曲线不总是那么标准,曲线也不总是那么光滑,比如这次的作业题,当处于欠拟合状态时,学习曲线看起来却没太大问题(?)

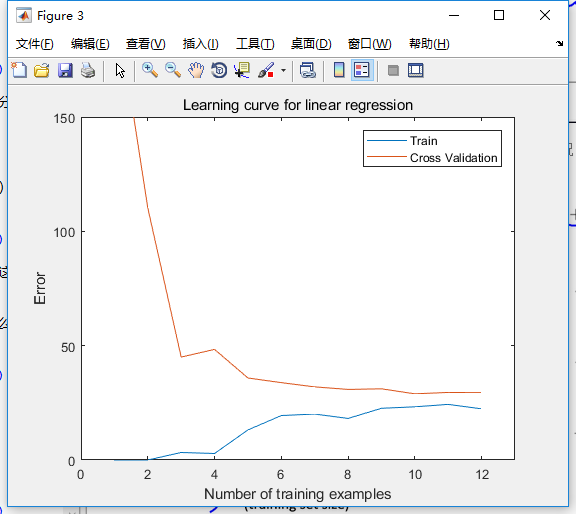
如上面两图,从第一幅图里可以判断是欠拟合,第二幅图却看不出问题。但如果对比着正常的拟合情况就会发现问题了。如下是特征增长处理后的拟合情况和学习曲线:

可以看到,正确的拟合情况下,学习曲线的训练误差趋于0,而交叉验证的曲线相对上面那种情况来讲会更低,而且可以判断的是,随着训练集的增加,验证曲线也会逐渐趋向训练曲线。
那么问题来了,针对作业题,过拟合情况是怎样的?之前正确拟合所设置的特征增长维度p=8,当我改为16时图像如下:
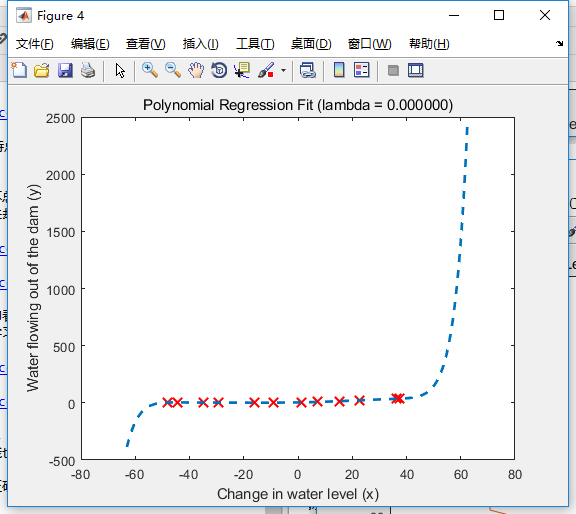
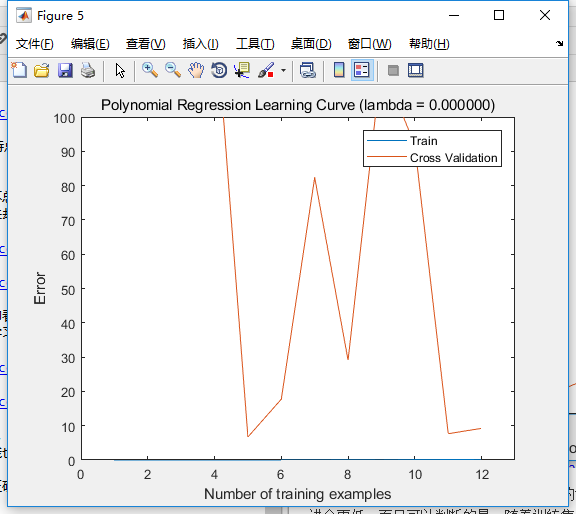
可以看到,学习曲线中,训练集误差还和之前一样趋于零,而交叉集的误差波动很大,看不出收敛趋势。
同时,我还发现三幅拟合曲线的纵轴分度各不相同。对于过拟合情况,我们可以判断,一小部分数据的微小干扰,根本不会影响整体的拟合特征。
另外,之所以两种情况训练误差都是0,个人分析原因是数据量太少。如果数据量加大,应该是过拟合趋于0,正常情况下有训练误差,但是误差很小。如果数据量扩大到现有的100倍,有可能过拟合所采用的特征维度才更合适。简而言之,数据量与相对应的合适特征维度应该是有一定的线性关系的。
模型选择
之前其实已经讨论过学习曲线和模型特征维度之间的关系,不过这里还是有必要再做一个总结,如下图:
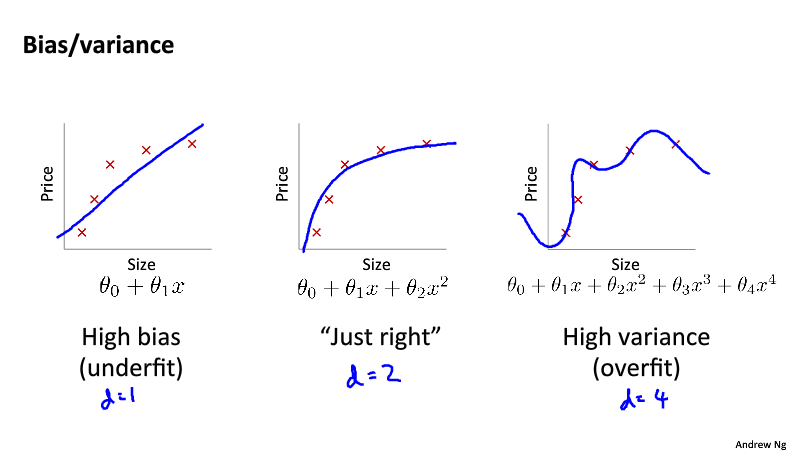
这是NG之前反复提及的拟合问题,只不过这次用了两个名词来表达——偏差和方差。可以看到,在同样的数据量下,模型维度过高过低都是不合适的。具体的模型维度与误差的关系曲线如下图:
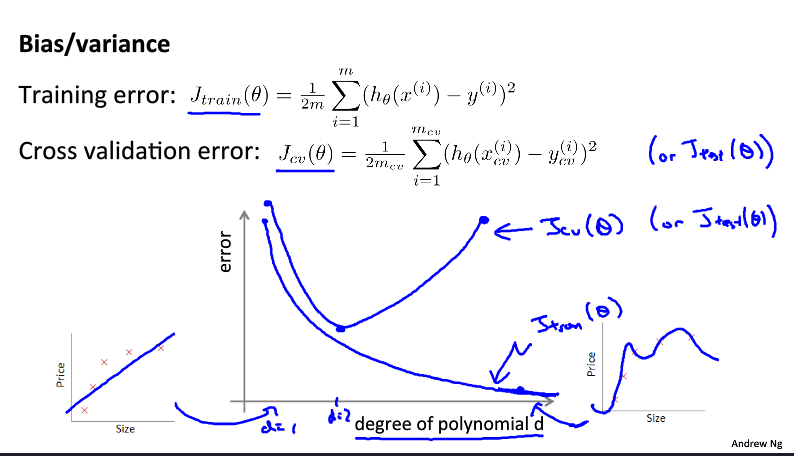
对于线性拟合问题,模型的选择其实就是特征维度的选择。在真实场景中,我们其实很难判断到底多少合适(如上)。好的做法应该是选择一定区间,一个一个跑一遍,比较它们学习曲线的优劣,就如同‘学习曲线’部分所分析的那样。
正则化
之前NG讲过,正则化同样可以解决偏差和方差的问题。也就是说,正则化可以在一定程度上修正训练集过少或特征维度过高,以及特征维度过低所产生的误差。针对之前作业例子中提到的欠拟合和过拟合问题,我们来进行正则化修正,看看效果如何。
修正过拟合问题
首先是过拟合问题,我们先根据如下曲线,选择一个最佳的正则化参数。
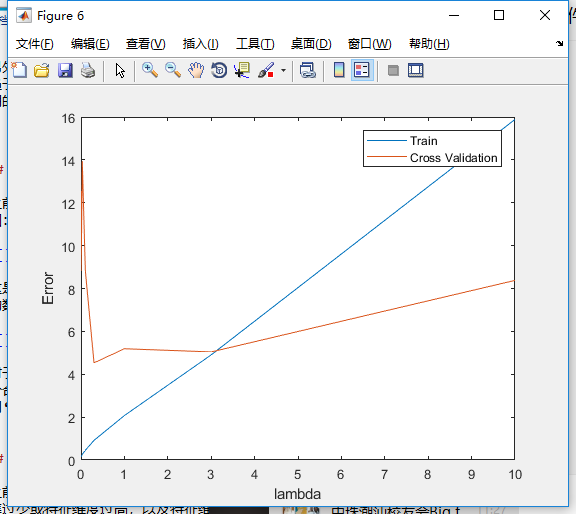
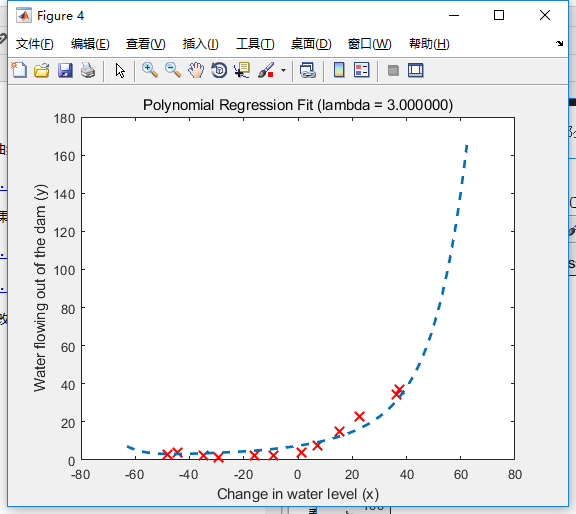
可以看到,(lambda=3)是比较合适的。那么我们就选择这个值,修正我们的模型。


拟合情况有所改善,之前一小部分数据的微小干扰,根本不会影响整体的拟合特征,现在已经好多了。另外学习曲线中交叉集误差波动的情况也修正了。可以说十分有效。
修正欠拟合问题
针对本例的欠拟合问题(p=1),我们先看下能不能根据曲线来选择正则化参数。
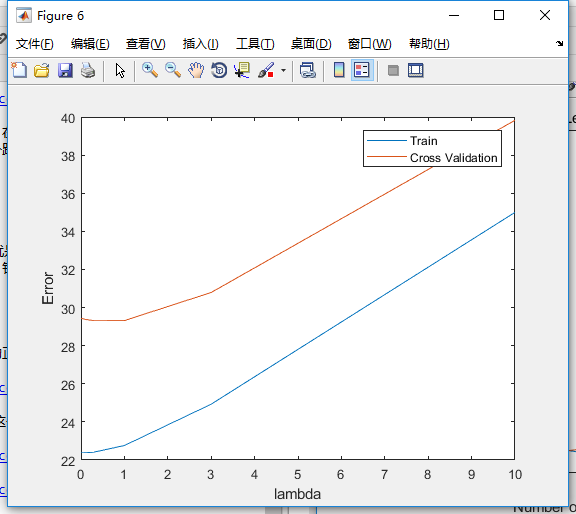
很遗憾的是,曲线不收敛,我们没法找出最佳参数。那如果我们试下(lambda=3)会怎样?
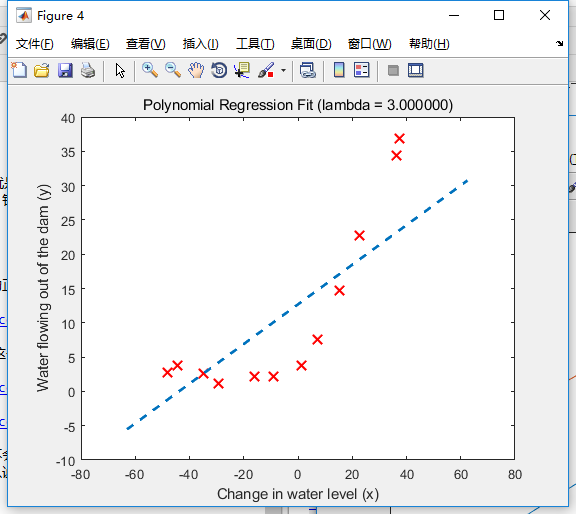
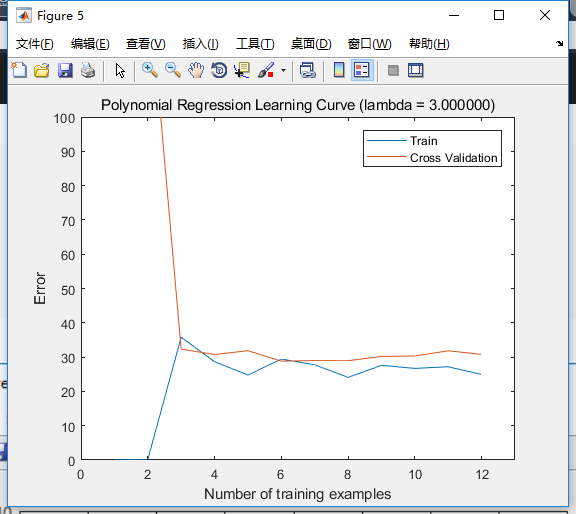
可以看到,无论是拟合情况还是学习曲线都没有得到明显改善。也就是说,本例中正则化无法修正误差,更合适的做法应该是进行适当的特征增长。
在选择合适模型下正则化
如果模型选择好了,正则化效果如何呢?如下两图:

比起没有正则化时,收敛的趋势更加明显。所以说还是很有效的。
数据随机化
作业题中有一道选作,是针对数据集很小的情况,让我们在训练过程中随机化数据,多次重复拟合并算出误差平均值。需要注意的是,这里每次运行得到的结果都是不同的,但是整体趋势还是稳定不变的。
这里网上很难找到选做题,我也是思考了很久,并且到处搜索,终于找到一篇博客,最终才写出可运行代码。下面贴出代码:
%% ==== Optional exercise 1: Computing test seterror =========
% find better lambda
index = 1;
min = exp(100);
for a = 1:length(lambda_vec)
if (min > abs(error_train(a) - error_val(a)))
min = abs(error_train(a) - error_val(a));
index = a;
end
end
lambda = lambda_vec(index);
m = size(X_poly, 1);
n = size(X_poly_test,1);
theta = trainLinearReg([ones(m, 1) X_poly], y, lambda);
error_test = linearRegCostFunction([ones(n, 1) X_poly_test], ytest, theta, 0);
fprintf('lambda: %f(this value should be about 3)
', lambda);
fprintf('error_test: %f(this value should be about 3.8599)
', error_test);
fprintf('Program paused. Press enter to continue.
');
pause;
%% =============== Optional exercise 2 ========================
% Plotting learningcurves with randomly selected examples
tic; % 开始计时
lambda = 0.01;
m = size(X, 1);
n = size(Xval, 1);
error_train = zeros(m, 1);
error_val = zeros(m, 1);
repeat = 50;
for i = 1:m
for time = 1:repeat
seq = randperm(m, i); % 随机化(1:m)序列并选出其中的i个
X_poly_rand = X_poly(seq,:);
y_rand = y(seq,:);
seq_val = randperm(n, i);
Xval_poly_rand = X_poly_val(seq_val,:);
yval_rand = yval(seq_val,:);
theta = trainLinearReg([ones(i, 1) X_poly_rand], y_rand, lambda);
J = linearRegCostFunction([ones(i, 1) X_poly_rand], y_rand, theta, 0);
Jval = linearRegCostFunction([ones(i, 1) Xval_poly_rand], yval_rand, theta, 0);
error_train(i) = error_train(i) + J;
error_val(i) = error_val(i) + Jval;
end
end
error_train = error_train / repeat;
error_val = error_val / repeat;
figure;
plot(1:m, error_train, 1:m, error_val);
title(sprintf('Polynomial Regression Learning Curve (lambda = %f)', lambda));
legend('Train', 'Cross Validation');
xlabel('Number of training examples');
ylabel('Error');
axis([0 13 0 100]);
toc; % 停止计时
fprintf('Program paused. Press enter to continue.
');
pause;
这个方法相比之前要运行很久,在我的小破本里一般要6-8分钟,算是让我体验到了机器学习过程中那种奇妙的期待感。
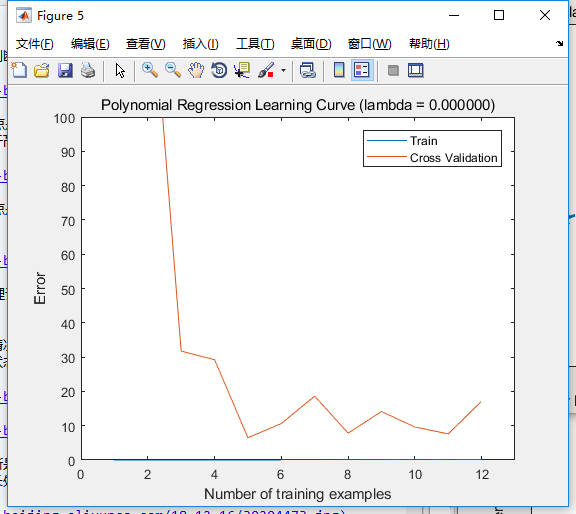
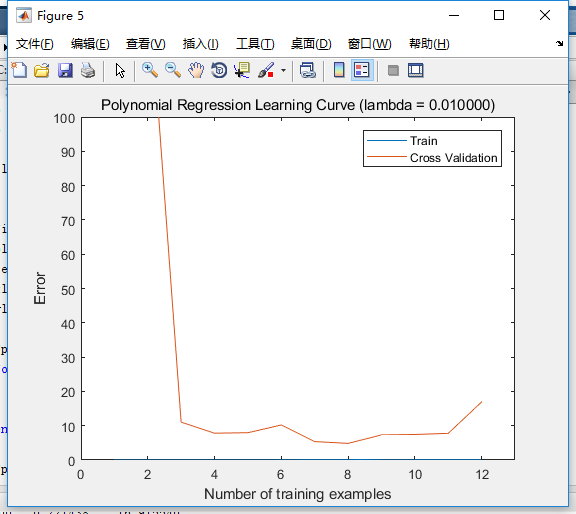
上面的代码,选择的参数p=8,(lambda=0.01),拟合次数为50次。最终得到的学习曲线如下图:

相比没有这么处理的情况,如下图,似乎更差了?不过还是可以发现,交叉集误差波动没那么大了,收敛的趋势也更加明显。
如果正则化参数为3,其它照旧时,这个方法的学习曲线如下:
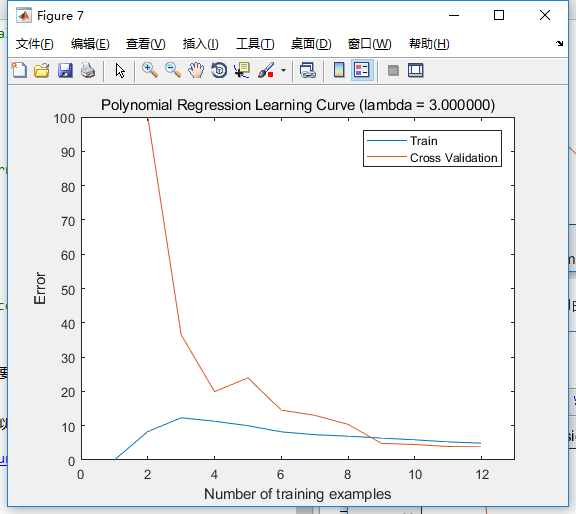
总而言之,这个方法是针对数据集量很少的情况,对于误差的计算会更加准确。
总结
本章其实只针对线性回归的拟合修正进行了讨论,当然,其中的一些思想对其它拟合方式也有效,比如说正则化在逻辑回归和简单的神经网络中也很有效。下面对线性回归拟合进行一般性步骤总结:
- 将总数据集合适划分。
- 选择合适区间,比较不同特征维度p的学习曲线和拟合情况,选择最合适的特征维度。
- 选择合适区间,比较不同正则化参数(lambda)的误差曲线,选择合适的正则化参数。
- 如果数据集很小的话,训练过程中尽量随机化数据,多次拟合并算出误差平均值。