1796.字符串中第二大的数字
解题思路
遍历这个字符串,维护两个两个值——第一大的数字和第二大的数字。
注意不存在第二大数字的时候要返回-1。
参考代码
class Solution { public int secondHighest(String s) { int maxx1 = -1 , maxx2 = -1; for(int i=0;i<s.length();i++){ char x = s.charAt(i); //获取当前下标的字符 if(x<'0'||x>'9') continue; //当前是字母 int now = x - '0'; //计算出当前字符代表的数字 if(now > maxx1){ //如果比第一大数字大,那么第一大就成第二大,当前数字为第一大 maxx2 = maxx1; maxx1 = now; } if(now > maxx2 && now < maxx1){//比第一大要小,但比第二大数字大 maxx2 = now; } } return maxx2; } }
1716.计算力扣银行的钱
解题思路1
我们对这n天一天天地模拟,计算出每一天应该加多少钱,然后统计进答案。
参考代码1
class Solution { public int totalMoney(int n) { int week = 1,num = 0; // week为当前星期一加的钱,num为当天应加的钱 int res = 0; for(int i=1;i<=n;i++){ if(i%7 == 1){ //当今天是星期一 num = week; week++; //下周一要比这周一多1块 } res += num; //统计答案 num++; //明天应该多加1块钱 } return res; } }
解题思路2
我们观察每一周加的总钱数:28 35 42
可以知道这是一个等差数列,我们可以使用等差数列的求和公式:
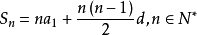
计算出前x周加的总钱数为28x +x(x-1)7/2
然后零散的几天,第一天加的钱数是n/7+1,最后一天为n/7+n%7,使用等差数列求和公式,一共是(n/7+1+n/7+n%7)(n%7)/2
参考代码2
class Solution { public int totalMoney(int n) { int a = n / 7, b = n % 7; //a为n有多少周,b为不足一周的剩余的天数 int ans = 28 * a + a * (a - 1) * 7 / 2 + (a + 1 + a + b) * b / 2; return ans; } }