【问题描述】
商店里出售n种不同品种的花。为了装饰桌面,你打算买m支花回家。你觉得放两支一样的花很难看,因此每种品种的花最多买1支。求总共有几种不同的买花的方案?答案可能很大,输出答案mod p的值。
【输入格式】
一行3个整数n,m,p,意义如题所述。
【输出格式】
一个整数,表示买花的方案数。
【输入输出样例1】
|
flower.in |
flower.out |
|
4 2 5 |
1 |
见选手目录下的flower / flower1.in与flower / flower1.out
【输入输出样例1说明】
用数字1,2,3,4来表示花的种类的话,4种花里买各不相同的2支的方案有(1,2)、(1,3)、(1,4)、(2,3)、(2,4)、(3,4),共6种方案,模5后余数是1。
【输入输出样例2】
见选手目录下的flower / flower2.in与flower / flower2.out
【数据范围】
对于30%的数据,n,m≤10
对于50%的数据,n,m≤1000
对于80%的数据,1≤m≤n≤50,000
对于100%的数据,1≤m≤n≤1,000,000,p≤1,000,000,000
思路:
对于公式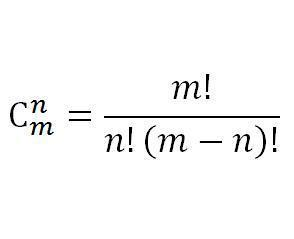 进行分解质因数处理用分子的每个质因数个数 减去 分母的质因数,最后快速幂乘起来。
进行分解质因数处理用分子的每个质因数个数 减去 分母的质因数,最后快速幂乘起来。
找质因数的时候,先筛出可能用到的质数,再应用下面的原理,就能很快求出,质因数个数了。
x!中质因数p的个数=【x/p】+[x/(p*p)】+【x/(p*p*p)】.......直到p^t>x .
.
详见《初等数论(闵嗣鹤、严士健)》函数【x】与{x}。
#include<iostream> #include<cstdio> #include<cstring> #include<queue> #include<algorithm> #include<vector> using namespace std; #define LL long long int n,m,p; int a[1000009]; int prime[200000];bool mark[1000009]; LL P; void innt() { for(int i=2;i<=n;i++) { if(!mark[i]) prime[++prime[0]]=i; for(int j=1;j<=prime[0];j++) { if(i*prime[j]>n) break; mark[i*prime[j]]=1; if(i%prime[j]==0) break; } } } void fen(int x,int y) { for(int i=1;i<=prime[0];i++) { P=prime[i]; while(P<=x) { a[i]+=1LL*y*(x/P); P*=prime[i]; } } } long long qm(LL a,LL b) { LL tot=1; while(b) { if(b&1) (tot*=a)%p; b/=2;a=(a*a)%p; } return tot; } int main() { freopen("flower.in","r",stdin); freopen("flower.out","w",stdout); scanf("%d%d%d",&n,&m,&p); innt(); fen(n,1);fen(m,-1);fen(n-m,-1); long long ans=1; for(int i=1;i<=prime[0];i++) ans=ans*qm(prime[i],a[i])%p; cout<<ans; }