概述
隐马尔可夫模型(hidden Markov model, HMM)是可用于标注问题的统计学习模型,描述由隐藏的马尔可夫链随机生成观测序列的过程,属于生成模型。
隐马尔科夫模型的基本概念
1、隐马尔科夫模型的定义
(1)定义10.1 (隐马尔可夫模型)
隐马尔可夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测而产生观测随机序列的过程。
隐藏的马尔可夫链随机生成的状态的序列,称为状态序列(state sequence)。每个状态生成一个观测,而由此产生的观测的随机序列,称为观测序列(observation sequenoe )。序列的每一个位置又可以看作是一个时刻。
(2)隐马尔可夫模型的形式定义
设Q是所有可能的状态的集合,V是所有可能的观侧的集合:![]() 。其中,N是可能的状态数,M是可能的观测数。
。其中,N是可能的状态数,M是可能的观测数。
I是长度为T的状态序列,O是对应的观测序列:![]() 。
。
隐马尔可夫模型由初始概率分布、状态转移概率分布以及观测概率分布确定。
①状态转移概率矩阵A:![]()
其中![]() 是在时刻t处于状态qi的条件下在时刻t+1转移到状态qj的概率。
是在时刻t处于状态qi的条件下在时刻t+1转移到状态qj的概率。
②观测概率矩阵B:![]()
其中![]() 是在时刻t处于状态qj的条件下生成观测vk的概率。
是在时刻t处于状态qj的条件下生成观测vk的概率。
③初始状态概率向量π:![]()
其中![]() 是时刻t=1处于状态qi的概率。
是时刻t=1处于状态qi的概率。
隐马尔可夫模型兄可以用三元符号表示,即![]() 。A,B,π称为隐马尔可夫模型的三要素。
。A,B,π称为隐马尔可夫模型的三要素。
状态转移概率矩阵A与初始状态概率向量π确定了隐藏的马尔可夫链,生成不可观测的状态序列。
观测概率矩阵B确定了如何从状态生成观测,与状态序列综合确定了如何产生观测序列。
(3)隐马尔可夫模型作了两个基本假设:
①齐次马尔可夫性假设,即假设隐藏的马尔可夫链在任意时刻t的状态只依赖于其前一时刻的状态,与其他时刻的状态及观测无关,也与时刻t无关。
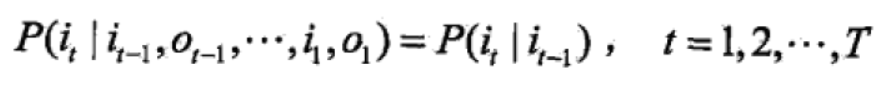
②观测独立性假设,即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态,与其他观测及状态无关。
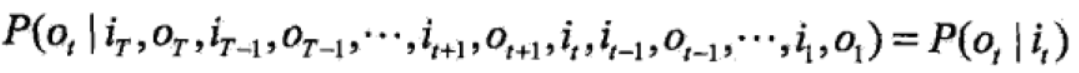
2、观测序列的生成过程

3、隐马尔可夫模型的3个基本问题
(1)概率计算问题。给定模型![]() 和观测序列
和观测序列![]() ,计算在模型lamda之下观测序列O出现的概率
,计算在模型lamda之下观测序列O出现的概率![]() 。
。
(2)学习问题。己知观测序列![]() ,估计模型
,估计模型![]() 参数,使得在该模型下观测序列概率
参数,使得在该模型下观测序列概率![]() 最大。即用极大似然估计的方法估计参数。
最大。即用极大似然估计的方法估计参数。
(3)预测问题。也称为解码(decoding)问题。己知模型![]() 和观测序列
和观测序列![]() ,求对给定观测序列条件概率
,求对给定观测序列条件概率![]() 最大的状态序列
最大的状态序列![]() ,即给定观测序列,求最有可能的对应的状态序列。
,即给定观测序列,求最有可能的对应的状态序列。
概率计算算法
(这个博客讲的清楚:https://blog.csdn.net/u013597931/article/details/80593210?tdsourcetag=s_pcqq_aiomsg)
1、直接计算法


2、前向算法
(1)前向概率定义

(2)观测序列概率的前向算法

3、后向算法
(1)后向概率定义

(2)观测序列概率的后向算法

4、直接计算、前向和后向算法例子
参见博客: https://blog.csdn.net/zhuqiang9607/article/details/83934961
5、一些概率和期望值的计算(前后向概率性质)



学习算法
隐马尔可夫模型的学习,根据训练数据是包括观测序列和对应的状态序列还是只有观测序列,可以分为监督学习与非监督学习。
1、监督学习方法
假设已给训练数据包含S个长度相同的观测序列和对应的状态序列![]() ,利用极大似然估计法来估计隐马尔可夫模型的参数。具体如下:
,利用极大似然估计法来估计隐马尔可夫模型的参数。具体如下:
(1)转移概率aij的估计
设样本中时t处于状态i时刻t+1转移到状态j的频数为Aij,那么状态转移概率的估计是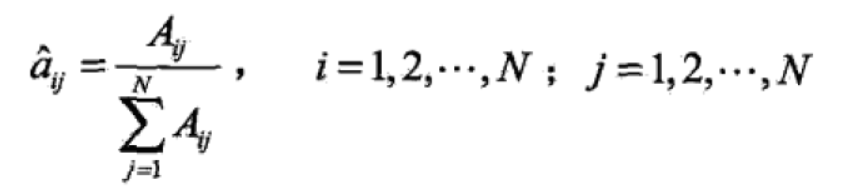
(2)观测概率bj(k)的估计
设样本中状态为j并观测为k的频数是Bjk,那么状态为j观测为k的概率的估计是
(3)初始状态概率πi的估计
初始状态概率πi的估计为S个样本中初始状态为qi的频率。
2、非监督学习算法——Baum-Welch算法
假设给定训练数据只包含S个长度为T的观测序列![]() 而没有对应的状态序列,目标是学习隐马尔可夫模型的参数。将观测序列数据看作观测数据O,状态序列数据看作不可观测的隐数据I,那么隐马尔可夫模型事实上是一个含有隐变量的概率模型:
而没有对应的状态序列,目标是学习隐马尔可夫模型的参数。将观测序列数据看作观测数据O,状态序列数据看作不可观测的隐数据I,那么隐马尔可夫模型事实上是一个含有隐变量的概率模型:
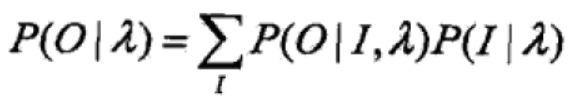
它的参数学习可以由EM算法实现,也就是说Baum-Welch算法是EM算法在隐马尔可夫模型中的具体实现。
(1)确定完全数据的对数似然函数
完全数据由观测数据和隐数据组成:![]()
其对数似然函数是![]()
(2)EM算法的E步:求Q函数![]()
有上述已知![]()
则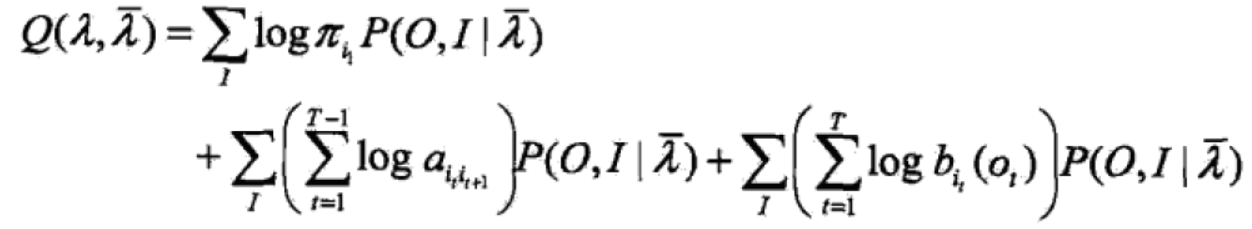
(3)EM算法的M步:极大化Q函数求模型参参数A,B,π(为避免班门弄斧,待细致推导后再补充)
①对上式第一项求最大值
得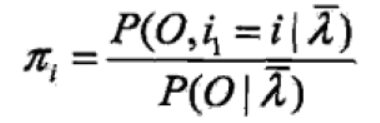
②对上式第二项求最大值
得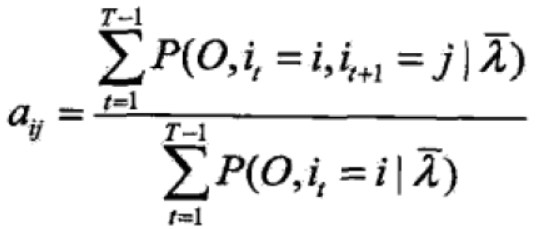
③对上式第三项求最大值
得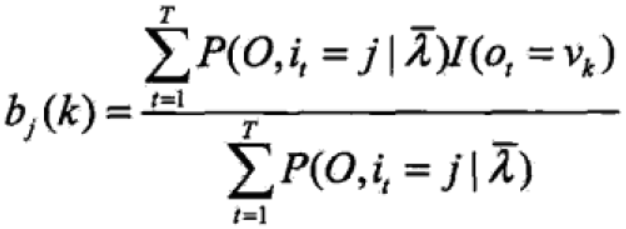
(4)把式子用之前前后向算法得到的各概率表示
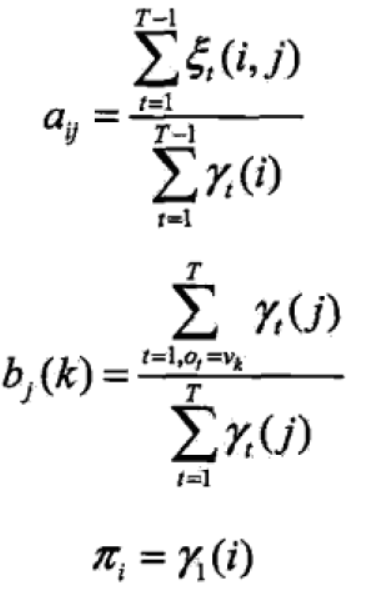
最后Baum-Welch算法总结如下:

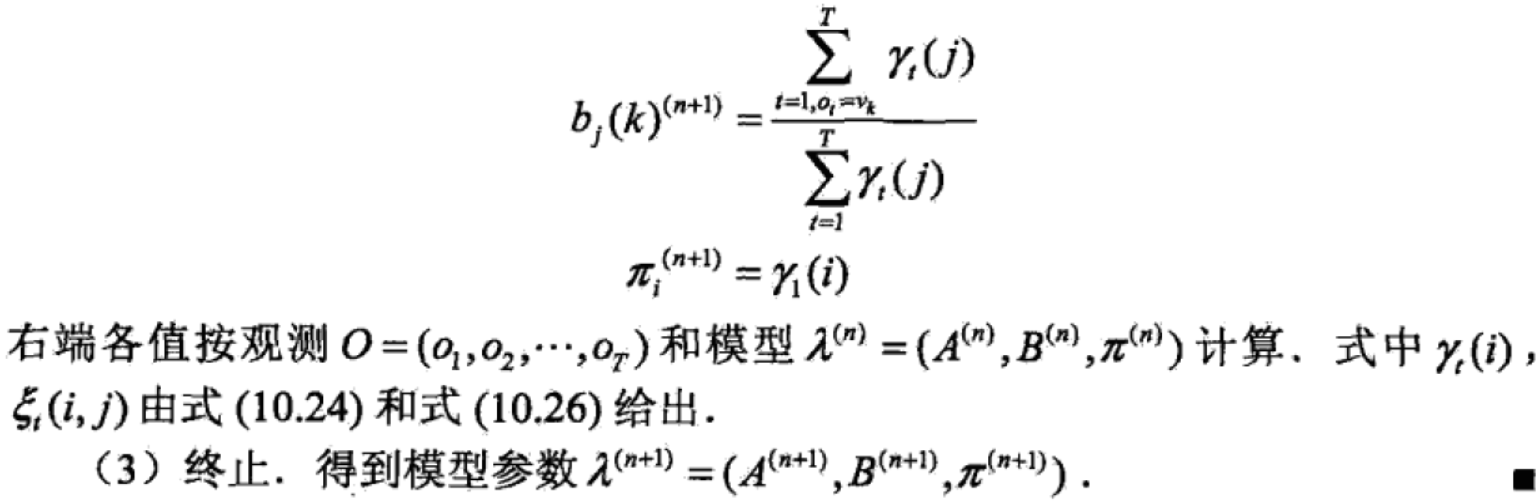
预测算法
隐马尔可夫模型预测的两种算法:近似算法与维特比算法(Viterbi algorithm)。
1、近似算法
(1)主要思想
在每个时刻t选择在该时刻最有可能出现的状态it*,得到一个状态序列![]() 作为预测的结果。
作为预测的结果。
(2)形式化表达
给定模型参数和观测序列,时刻t处在状态qi的概率为: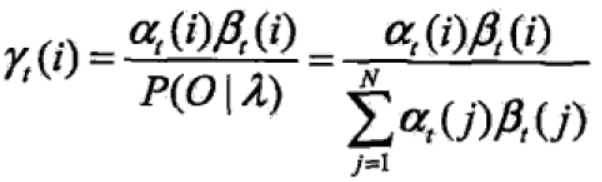
在每一时刻t最有可能的状态it*通过下式得到:![]()
(3)优缺点
近似算法的优点是计算简单,其缺点是不能保证预测的状态序列整体是最有可能的状态序列,因为预测的状态序列可能有实际不发生的部分。该方法得到的状态序列中有可能存在转移概率为0的相邻状态。
2、维特比算法
(1)主要思想
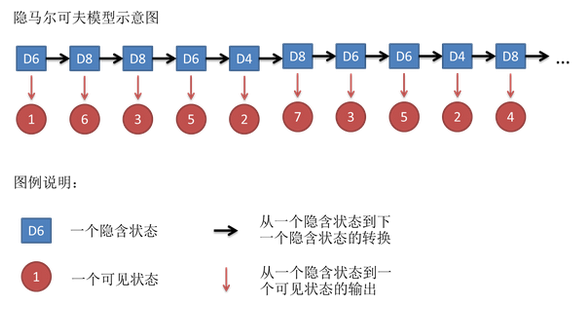
维特比算法实际是用动态规划解隐马尔可夫模型预侧问题,即用动态规划(dynamic programming)求概率最大路径(最优路径)。一条路径对应着一个状态序列。
根据动态规划原理,最优路径具有这样的特性:如果最优路径在时刻t通过结点it*,那么这一路径从结点it*到终点iT*的部分路径,对于从it*到iT*的所有可能的部分路径来说,必须是最优的。
依据这一原理,我们只需从时刻t=1开始,递推地计算在时刻t状态为i的各条部分路径的最大概率,直至得到时刻t=T状态为i的各条路径的最大概率。时刻t=T的最大概率即为最优路径的概率P*。最优路径的终结点iT*也同时得到。
之后,为找到最优路径的各个节点,从终结点iT*开始,由后向前逐步求得结点iT-1* , ... , i1*。这就是维特比算法。
(2)两个变量

理解请看这里:https://www.zhihu.com/question/20136144
(3)维特比算法

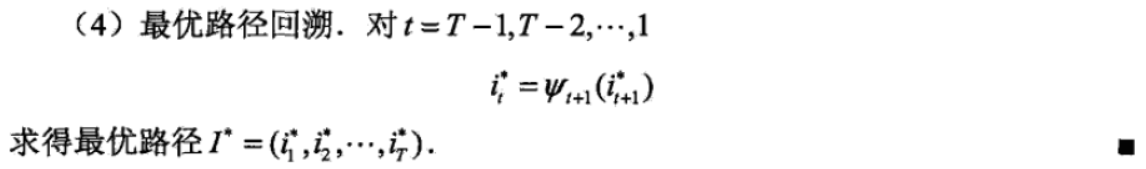
(4)一个例子