实验二 动态分区分配方式的模拟
一、实验目的
了解动态分区分配方式中的数据结构和分配算法,并进一步加深对动态分区存储管理方式及其实现过程的理解
二、实验内容
- 用C语言分别实现采用首次适应算法和最佳适应算法的动态分区分配过程和回收过程。其中,空闲分区通过空闲分区链(表)来管理;在进行内存分配时,系统优先使用空闲区低端的空间。
- 假设初始状态下,可用的内存空间为640KB,并有下列的请求序列:
•作业1申请130KB
•作业2申请60KB
•作业3申请100KB
•作业2释放60KB
•作业4申请200KB
•作业3释放100KB
•作业1释放130KB
•作业5申请140KB
•作业6申请60KB
•作业7申请50KB
•作业8申请60KB
请分别采用首次适应算法和最佳适应算法进行内存的分配和回收,要求每次分配和回收后显示出空闲内存分区链的情况。
三、实现思路
首次适应算法中空闲区的排列顺序是按地址大小排列,小地址在前,大地址在后;而最佳适应算法中空闲区的队列排列是空闲区块的大小,小的在前,大的在后。
用了一个结构体来存储空闲区的信息,然后再用双链表来实现空闲区队列
四、主要的数据结构(展开批注可显示代码)
1、内存分区链表定义[c1]
[c1]#include <iostream> using namespace std; const int Max_length=640;//最大内存 int a, b;//a记录算法编号,b记录操作编号 struct freearea//空闲区的结构体 { int ID;//分区号 int size;//分区大小 int address;//分区地址 bool flag;//使用状态,0为未占用,1为已占用 }; typedef struct DuNode//双向链表结点 { freearea data;//数据域 DuNode *prior;//指针域 DuNode *next; }*DuLinkList; DuLinkList m_rid = new DuNode, m_last = new DuNode;//双向链表首尾指针 void init()//空闲区队列初始化 { m_rid->prior = NULL; m_rid->next = m_last; m_last->prior = m_rid; m_last->next = NULL; m_rid->data.size = 0; m_last->data.address = 0; m_last->data.size = Max_length; m_last->data.ID = 0; m_last->data.flag = 0;//!!! }
2、分区状态定义[c1]
[c1]void show() { DuNode *p = m_rid->next;//指向空闲区队列的首地址 cout << "+++++++++++++++++++++++++++++++++++++++" << endl; while (p) { cout << "分区号: "; if (p->data.ID == 0) cout << "FREE" << endl; else cout << p->data.ID << endl; cout << "分区起始地址: " << p->data.address << endl; cout << "分区大小: " << p->data.size << endl; cout << "分区状态: "; if (p->data.flag) cout << "已被占用" << endl; else cout << "空闲" << endl; cout << "——————————————————" << endl; p = p->next; } }
3、首次适应算法函数定义[c1]
[c1]bool first_fit(int id,int m_size)//首次适应算法 { DuNode *p = m_rid->next;//指向空闲区队列的首地址 DuLinkList fa = new DuNode;//新建一个空闲区并赋值 //memset(fa, 0, sizeof(DuNode)); fa->data.ID = id; fa->data.size = m_size; fa->data.flag = 1;//表示被占用 while (p)//在空闲区列表中从低地址向高地址查找 { if (p->data.size >= m_size && !p->data.flag)//找到大于等于所需的内存的空闲区 { if (p->data.size == m_size)//刚好空闲区大小与所需大小相等 { p->data.ID = id; p->data.flag = 1; free(fa);//清空新创建的空闲区 return true; } else if(p->data.size>m_size)//空闲区比所需内存大,则需要将多的内存作回收处理 { fa->data.address = p->data.address;//将空闲区的前半部分分出去 p->data.address += m_size; p->data.size -= m_size; p->prior->next = fa; fa->next = p; fa->prior = p->prior; p->prior = fa; return true; } } p = p->next; } free(fa);//查找分配失败 return false; }
4、最佳适应算法函数定义[c1]
bool best_fit(int id, int m_size)//最佳适应算法,其中需要查找最佳的存放位置 { DuNode *p = m_rid->next;//指向空闲区队列的首地址 DuNode *q = NULL;//存放最佳地址 DuLinkList fa = new DuNode;//新建一个空闲区并赋值 memset(fa, 0, sizeof(DuNode)); fa->data.ID = id; fa->data.size = m_size; fa->data.flag = 1;//表示被占用 int d = Max_length;//所需内存大小与空闲区大小之间的差值 while (p)//循环查找最小的差值d并记录此时的地址值 { if (p->data.size >= m_size && !p->data.flag)//找到大于等于所需的内存的空闲区 { if (p->data.size - m_size < d) { q = p; d = q->data.size - m_size; } } p = p->next; } if (q == NULL)//查找分配失败 return false; else { if (d == 0)//刚好找到与所需内存大小一样的空闲区 { p->data.ID = id; p->data.flag = 1; free(fa);//清空新创建的空闲区 return true; } else//空闲区比所需内存大,则需要将多的内存作回收处理 { fa->data.address = q->data.address;//将空闲区的前半部分分出去 q->data.address += m_size; q->data.size -= m_size; q->prior->next = fa; fa->next = q; q->prior = fa; fa->prior = q->prior; return true; } } }
5、内存分配函数定义[c1]
[c1]bool allocation()//分配资源 { int id, m_size;//输入的作业号和内存块大小 cout << "请输入作业编号(分区号)和申请的内存大小(KB):"; cin >> id >> m_size; if (m_size <= 0)//申请的内存大小小于等于0,申请失败 { cout << "申请的内存大小错误!请重新输入" << endl; return false; } if (a == 1)//首次适应算法 { if (first_fit(id, m_size)) { cout << "内存分配成功!" << endl; show();//显示内存分布 } else cout << "内存不足,分配失败!" << endl; return true; } if (a == 2)//最佳适应算法 { if (best_fit(id, m_size)) { cout << "内存分配成功!" << endl; show();//显示内存分布 } else cout << "内存不足,分配失败!" << endl; return true; } }
6、内存回收函数定义[c1]
[c1]void recycle()//回收内存 { int id; cout << "请输入想要释放的作业号:"; cin >> id; DuNode *p = m_rid->next;//指向空闲区队列的首地址 DuNode *p1 = NULL;//辅助向量 while (p)//查找需要释放的作业的地址并进行合并工作 { if (p->data.ID == id) { p->data.ID = 0; p->data.flag = 0; if (!p->prior->data.flag)//与前一个空闲区相邻,则合并 { p->prior->data.size += p->data.size; p->prior->next = p->next; p->next->prior = p->next; } if (!p->next->data.flag)//与后一个空闲区相邻,则合并 { p->data.size += p->next->data.size; p->next->next->prior = p; p->next = p->next->next; } break; } p = p->next; } show(); }
7、主函数[c1]
[c1]void main() { cout << "******************动态分区分配模拟******************" << endl; cout << "**********1.首次适应算法 2.最佳适应算法**********" << endl; cout << "请输入要选择的分配算法:"; cin >> a; init();//初始化内存块 while (a != 1 && a != 2) { cout << "输入错误!请重新输入:" << endl; cin >> a; } while (1) { cout << "****************************************************" << endl; cout << "**********1.申请内存 2.释放内存 3.退出**********" << endl; cout << "请输入操作数:"; cin >> b; switch (b) { case 1: allocation(); break; case 2: recycle(); break; case 3: default: cout << "动态分区分配算法结束,再会!" << endl; exit(1); break; } } }
五、算法流程图
首次适应算法:
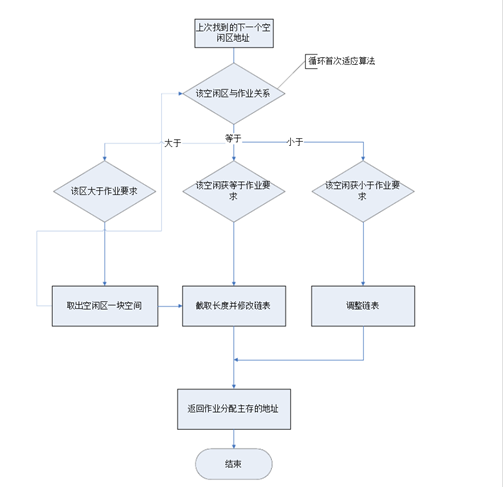
最佳适应算法:
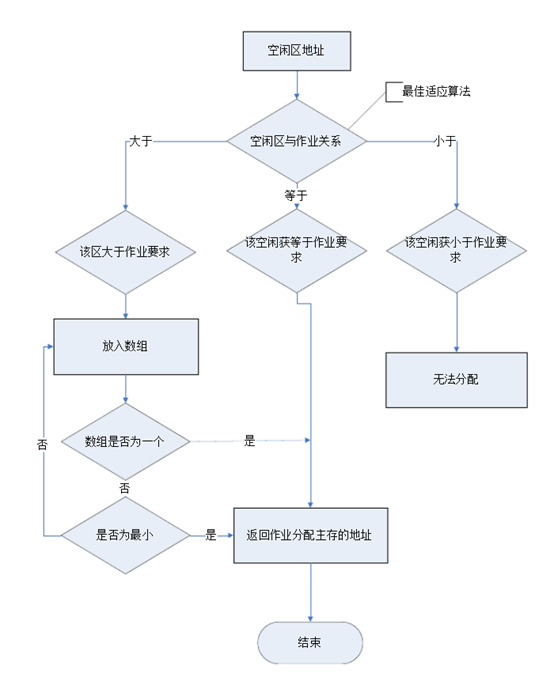
六、运行与测试
首次适应算法:
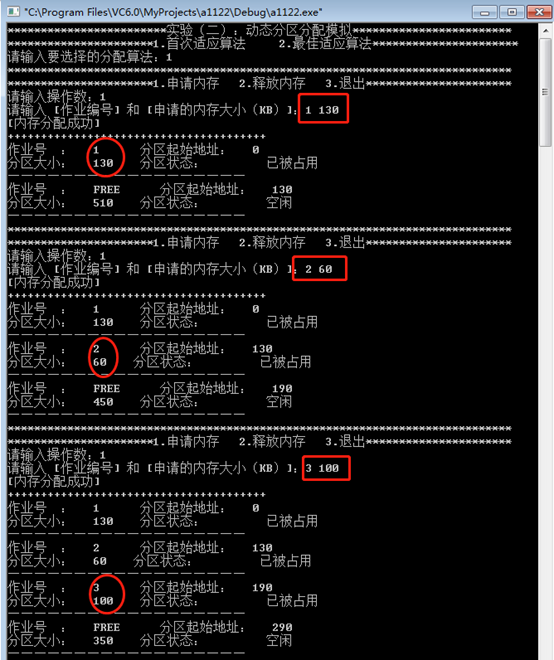
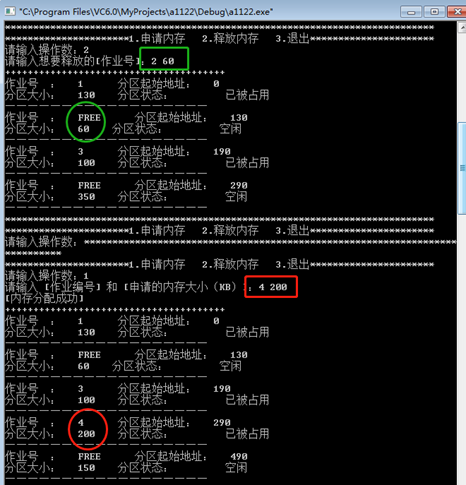
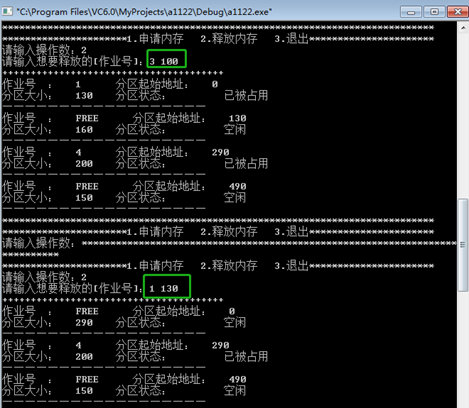
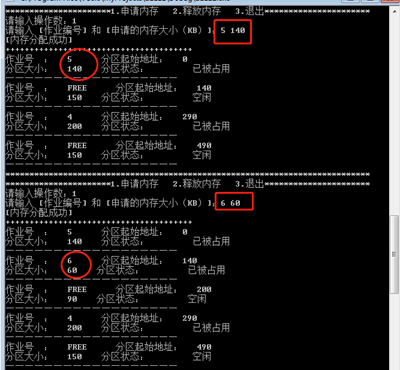
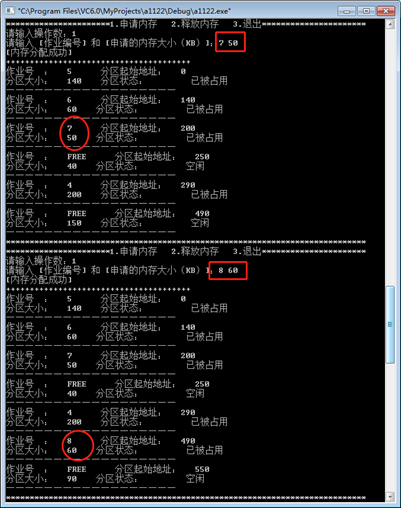
最佳适应算法:
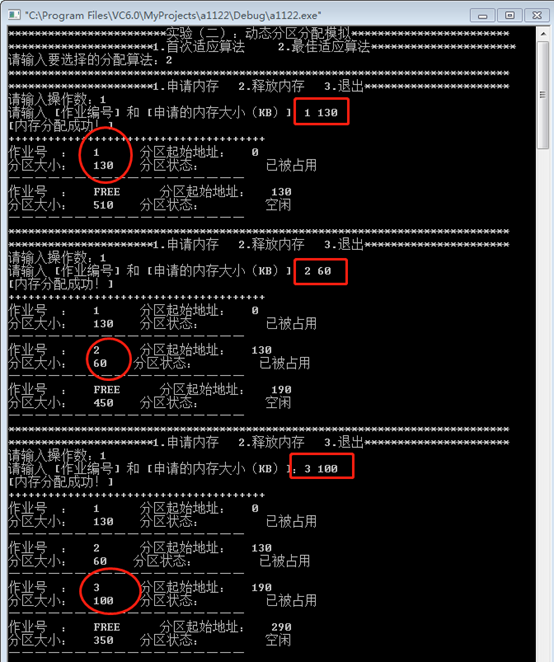
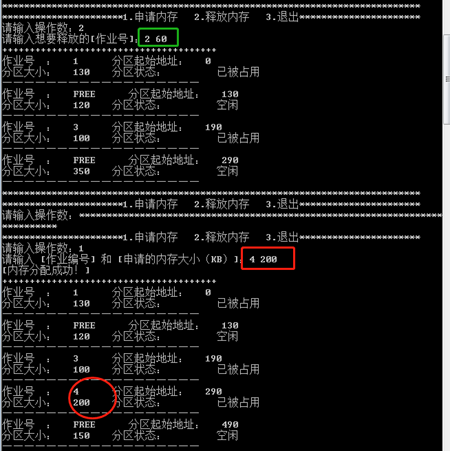
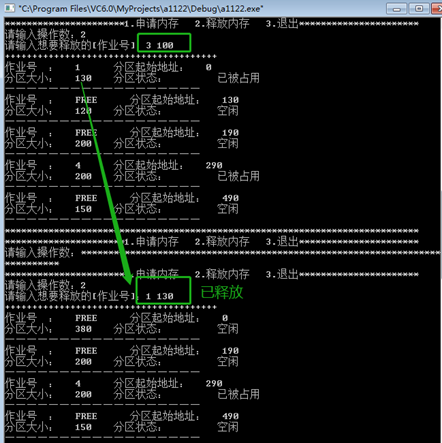

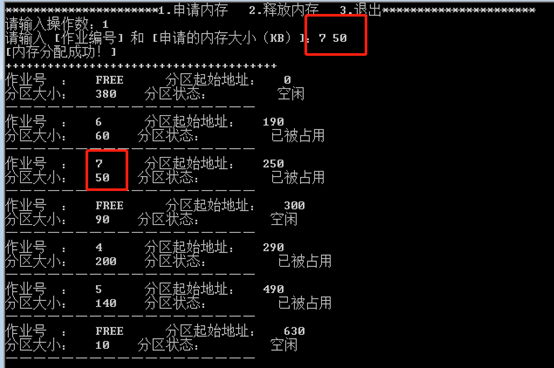
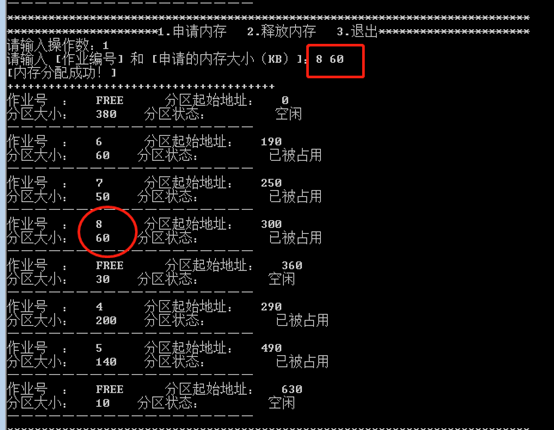
七、总结
思考:讨论各种分配算法的特点。
一、 首次适应算法(First Fit):
该算法从空闲分区链首开始查找,直至找到一个能满足其大小要求的空闲分区为止。然后再按照作业的大小,从该分区中划出一块内存分配给请求者,余下的空闲分区仍留在空闲分区链中。
特点: 该算法倾向于使用内存中低地址部分的空闲区,在高地址部分的空闲区很少被利用,从而保留了高地址部分的大空闲区。显然为以后到达的大作业分配大的内存空间创造了条件。
缺点:低地址部分不断被划分,留下许多难以利用、很小的空闲区,而每次查找又都从低地址部分开始,会增加查找的开销。
二、 最佳适应算法(Best Fit):
该算法总是把既能满足要求,又是最小的空闲分区分配给作业。为了加速查找,该算法要求将所有的空闲区按其大小排序后,以递增顺序形成一个空白链。这样每次找到的第一个满足要求的空闲区,必然是最优的。孤立地看,该算法似乎是最优的,但事实上并不一定。因为每次分配后剩余的空间一定是最小的,在存储器中将留下许多难以利用的小空闲区。同时每次分配后必须重新排序,这也带来了一定的开销。
特点:每次分配给文件的都是最合适该文件大小的分区。
缺点:内存中留下许多难以利用的小的空闲区。