[题解] [NOIP2013 提高组] 货车运输

前言

使用算法：堆优化 (prim) ， (LCA) 。

大样例

题目链接

题意

共有 (n) 个点，有 (m) 条边来连接这些点，每条边有权值。有 (q) 条类似于 (u) (v) 询问，求一条从 (u) 到 (v) 的路径使得路径上的最小权值最大，求这个最大值。若不存在从 (u) 到 (v) 的路径，则输出 (-1) 。

思路

先求该图的最大生成树，因为需要使得该路径上的最小值最大，而这条路径就是最小生成树的中两点的简单路径（最大生成树尽量取最大的边）。

故而，查询时的路径确定了，那么现在就是求这条路径的最小值了。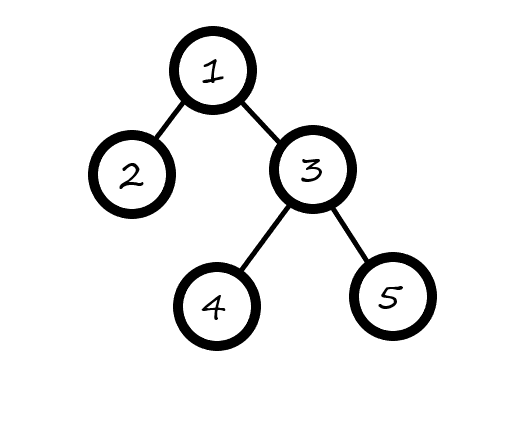
树上的距离操作离不开 (LCA) 。

假设查询 (2) 和 (4) 之间的距离最小值。那么它们之间的简单路径为 (2->1->3->4) ，可以分为两段：(s->lca) 和 (lca->t) 。这就是两条链，可以使用倍增求解。两条链的最小值一起来求最小值即可。

查询两个点是否在路径很简单，就是判断他们是否在一个连通块，直接在处理 (prim) 时一起求解即可。

C++代码

#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
using namespace std;
#define INF 0x3f3f3f3f
#define Swap(a, b) (a ^= b ^= a ^= b)
#define Min(a, b) ((a) < (b) ? (a) : (b)) 
void Quick_Read(int &N) {
	N = 0;
	int op = 1;
	char c = getchar();
	while(c < '0' || c > '9') {
		if(c == '-')
			op = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9') {
		N = (N << 1) + (N << 3) + (c ^ 48);
		c = getchar();
	}
	N *= op;
}
const int MAXN = 1e4 + 5;
const int MAXM = 40;
struct Node {
	int to, dist;
	Node() {}
	Node(int T, int D) {
		to = T;
		dist = D;
	}
	friend bool operator < (Node x, Node y) {
		return x.dist < y.dist;
	}
};
int fa[MAXN][MAXM], minn[MAXN][MAXM];
int de[MAXN];
vector<Node> v[MAXN];
priority_queue<Node> q;
bool vis[MAXN];
int dis[MAXN], belong[MAXN];
int ans, tot;
int n, m, t;
int LCA(int x, int y) {
	if(de[x] < de[y])
		Swap(x, y);
	for(int i = 30; i >= 0; i--)
		if(de[x] - (1 << i) >= de[y])
			x = fa[x][i];
	if(x == y)
		return x;
	for(int i = 30; i >= 0; i--) {
		if(fa[x][i] != fa[y][i]) {
			x = fa[x][i];
			y = fa[y][i];
		}
	}
	return fa[x][0];
}
int Climb(int x, int y) {
	int res = INF;
	for(int i = 30; i >= 0; i--)
		if(de[x] - (1 << i) >= de[y]) {
			res = Min(res, minn[x][i]);
			x = fa[x][i];
		}
	return res;
}
void Prim(int s) {
	tot++;
	dis[s] = 0;
	q.push(Node(s, 0));
	fa[s][0] = s;
	while(!q.empty()) {
		int now = q.top().to, adddist = q.top().dist;
		q.pop();
		if(vis[now])
			continue;
		belong[now] = tot;
		ans += adddist;
		vis[now] = true;
		int SIZ = v[now].size();
		for(int i = 0; i < SIZ; i++) {
			int next = v[now][i].to;
			if(v[now][i].dist > dis[next] && !vis[next]) {
				fa[next][0] = now;
				de[next] = de[now] + 1;
				minn[next][0] = v[now][i].dist;
				dis[next] = v[now][i].dist;
				q.push(Node(next, dis[next]));
			}
		}
	}
}
void Query() {
	int A, B;
	Quick_Read(t);
	for(int i = 1; i <= t; i++) {
		Quick_Read(A);
		Quick_Read(B);
		if(belong[A] != belong[B])
			printf("-1
");
		else {
			int lca = LCA(A, B);
			int ans1 = Climb(A, lca);
			int ans2 = Climb(B, lca);
			printf("%d
", Min(ans1, ans2));
		}
	}
}
void Build() {
	memset(dis, 128, sizeof(dis));
	for(int i = 1; i <= n; i++)
		if(!vis[i])
			Prim(i);
	for(int j = 1; j < 31; j++)
		for(int i = 1; i <= n; i++) {
			fa[i][j] = fa[fa[i][j - 1]][j - 1];
			minn[i][j] = Min(minn[fa[i][j - 1]][j - 1], minn[i][j - 1]);
		}
}
void Read() {
	int A, B, C;
	Quick_Read(n);
	Quick_Read(m);
	for(int i = 1; i <= m; i++) {
		Quick_Read(A);
		Quick_Read(B); 
		Quick_Read(C);
		v[A].push_back(Node(B, C));
		v[B].push_back(Node(A, C));
	}
}
int main() {
	Read();
	Build();
	Query();
	return 0;
}