[算法] 矩阵以及运用

首先来认识什么是矩阵

定义：

在数学中，矩阵是一个按照长方阵列排列的复数或实数集合
这是一个很简单的定义。

矩阵的运算

矩阵加减法

对于两个相同大小的矩阵，直接把相同位置的元素相加即可，如下图：

（这个好像并没有什么用）

重点来了

矩阵乘法

对于两个矩阵，当且仅当其中一个矩阵的行与另一个矩阵的列时，两个矩阵相乘才有意义。
设(A)为(P×M)的矩阵，(B)为(M×Q)的矩阵，我们用一个矩阵(C)来存储矩阵(A)与矩阵(B)的乘积。
定义在矩阵乘法中，结果(C)矩阵的第(i)行第(j)列的数，就是由矩阵(A)第(i)行 (M)个数与矩阵(B)第(j)列(M)个数分别相乘再相加得到的
即：其中矩阵(C)中的第(i)行第(j)列元素可以表示为：

那么答案矩阵就可以表示成

举个例子

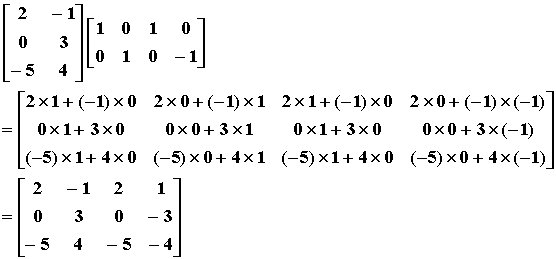
c++代码实现:

#include <cstdio>
#include <cstring>
const int MAXN = 1e3 + 5;
struct Matrix {
	int mar[MAXN][MAXN];
	int n, m;
	Matrix() { memset(mar, 0, sizeof(mar)); }
	void Matrix_Read() { //输入矩阵
		for(int i = 0; i < n; i++) 
			for(int j = 0; j < m; j++)
				scanf("%d", &mar[i][j]);
	}
	void Matrix_Write() { //输出矩阵
		for(int i = 0; i < n; i++) {
			for(int j = 0; j < m; j++)
				printf("%d ", mar[i][j]);
			printf("
");
		}
	}
	friend Matrix operator * (Matrix x, Matrix y) { //重载乘号并存储结果
		Matrix res; res.n = x.n; res.m = y.m;
		int sum;
		for(int i = 0; i < x.n; i++) {
			for(int j = 0; j < y.m; j++) {
				sum = 0;
				for(int k = 0; k < x.m; k++)
					sum += x.mar[i][k] * y.mar[k][j];
				res.mar[i][j] = sum;
			}
		}
		return res;
	}
};
Matrix A, B, C;
int main() {
	scanf("%d %d", &A.n, &A.m); B.n = A.m;
	A.Matrix_Read();
	scanf("%d", &B.m);
	B.Matrix_Read();
	C = A * B;
	C.Matrix_Write();
	return 0;
}

输入：

2 3
1 2 3
3 2 1
2 
1 1
2 2
3 3

输出：

2 3
1 2 3
3 2 1
2 
1 1
2 2
3 3

重要性质：

矩阵乘法能很好地运用是因为矩阵乘法支持乘法交换律
即是：
(A×(B×C) =(A×B)×C)

运用

可以很大程度上优化动态规划时的过程。
就拿斐波拉契数列来举例：
(f(i)=f(i-1)+f(i-2);(i≤3))
很容易就想到一项一项地递推，时间复杂度为(O(n))。
但如果(n)达到(1e18)甚至更大的时候，可能跑一个上午都跑不出来。
这时候就可以使用矩阵加速。
我们定义一个矩阵([f(n-2),f(n-1)])，我们希望得到(f(n))，即需要([f(n-1),f(n)])，需要另一个矩阵来乘上([f(n-2),f(n-1)])。
因为(f(n)=f(n-1)+f(n-2))矩阵第一列应该是：

同理，矩阵第二列为：

所以

对于任意一个(n(n≥3))有，第(n)项为

其中矩阵([1, 1])表示([f(1), f(2)])

C++实现

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define ll long long
ll N, MOD;
struct Matrix {
	ll mar[5][5];
	ll n, m;
	Matrix() { memset(mar, 0, sizeof(mar)); }
	void Matrix_Read() {
		for(ll i = 0; i < n; i++) 
			for(ll j = 0; j < m; j++)
				scanf("%lld", &mar[i][j]);
	}
	void Matrix_Write() {
		for(ll i = 0; i < n; i++) {
			for(ll j = 0; j < m; j++)
				printf("%lld ", mar[i][j]);
			printf("
");
		}
	}
	friend Matrix operator * (Matrix x, Matrix y) {
		Matrix res; res.n = x.n; res.m = y.m;
		ll sum;
		for(ll i = 0; i < x.n; i++) {
			for(ll j = 0; j < y.m; j++) {
				sum = 0;
				for(ll k = 0; k < x.m; k++)
					sum = (sum + x.mar[i][k] * y.mar[k][j]) % MOD;
				res.mar[i][j] = sum;
			}
		}
		return res;
	}
};
Matrix model, Fib;
void Init();
void Run();
Matrix Power(ll);
int main() {
	scanf("%lld %lld", &N, &MOD);
	Init();
	Run();
	return 0;
}
void Init() {
	Fib.mar[0][0] = 1;
	Fib.mar[0][1] = 1;
	model.mar[0][1] = 1;
	model.mar[1][0] = 1;
	model.mar[1][1] = 1;
	Fib.n = 1;
	Fib.m = model.n = model.m = 2;
}
void Run() {
	N -= 2;
	while(N) {
		if(N & 1)
			Fib = Fib * model;
		model = model * model;
		N >>= 1;
	}
	printf("%lld", Fib.mar[0][1] % MOD);
}

输入(n, m)
输出斐波拉契第(n)项对(m)取模后的值