字符串匹配KMP算法

【1】字符串匹配问题分析

（1）字符串匹配一般算法 与 KMP算法比较：

一般算法：从父串的第一个字符开始与子串的第一个字符开始比较：

1、若相等，再比较各自的第二个字符，依次循环进行，直到整个子串结束。在子串没有完全匹配完之前，若有一个字符不相等。请参考以下若不相等。

2、若不相等，从父串的第二个字符开始与子串的第一个字符开始重新逐个比较。如此循环，直至匹配到 完全子串 或 父串结束 程序结束。

KMP算法：观察分析子串的特点，我们很容易的发现子串中也存在相同的子串，如“ABCDABD”。

子串的前两位（str[0]、str[1]）字符AB与第五、六位（str[4]、str[5]）的AB字符就是相同的子串。

一般算法执行子串与父串匹配的过程中，假设当匹配到子串第七位（str[6]）处发现不相等时：

一般算法的做法：傻瓜式的用子串与从本次循环父串开始位的下一位重新执行新一轮逐位循环匹配。

KMP算法的做法：结合子串的特征，从开始位 + 4索引处重新又开始一轮的循环匹配。

或者，KMP算法的做法也可以理解为：从父串的匹配失败位开始与子串的第三位（str[2]）重新新一轮的匹配。

（2）KMP算法匹配过程如下：

2.1、待匹配父串、子串：

2.2、从父串第一个字符开始，B与A不匹配。

2.3、逐位进行匹配，B与A不匹配。

2.4、中间的循环匹配省略。直接到如下图所示，发现空字符与D不匹配。

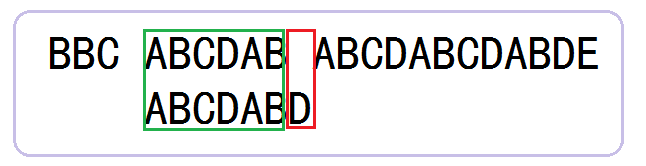
2.5、一般方法做法，从父串的第六个字符B开始，与子串的第一个字符A重新开始下一轮匹配。

KMP算法的做法如下，直接从父串的失败位空字符与子串的第三个字符C开始作比较，发现不匹配。

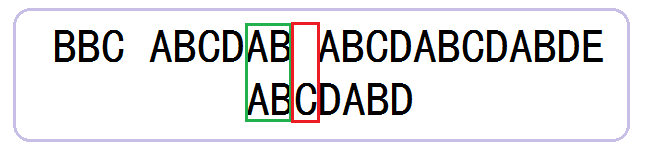
2.6、从父串的失败位空字符开始，与子串的第一个字符A开始，逐位重新开始循环匹配。

2.7、上一步发现空字符与A不匹配。那么，从主串空字符的下一位A开始与子串的第一个字符A进行新一轮循环匹配。

2.8、结果发现C字符与D字符不匹配。那么，KMP算法直接用失败位字符C与子串的第三个字符C开始匹配。

直至子串完全匹配。程序结束。

KMP算法是对子串进行规律性的分析后减少不必要循环过程的方法。

【2】各种算法C++实现

算法实现以及测试程序如下：

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <memory.h>

//第一种最普通的方法
//思路分析：
//(1) 确定父串与子串的长度大小
//(2) 定位父串，进入循环
//(3) 定位子串，进入循环
//(4) 开始逐个与父串比较，若有一个不相等，break;
//(5) 若完全匹配则成功
//(6) 返回索引

int FindStr1(const char *si, const char *sd)
{
    int m = strlen(si);
    int n = strlen(sd);
    int i = 0, j = 0, k = 0;
    for (i = 0; i <= m - n; ++i)
    {
        for (k = i, j = 0; j < n; ++j, ++k)
        {
            if (si[k] != sd[j])
            {
                break;
            }    
        }
        if (j >= n)
            return i;
    }

    return -1;
}

//第二种简单的方法(简称:巧借驱动)
//思想分析：
//(1) 定位父串与子串的索引
//(2) 锁定父串的索引指针,借子串的索引指针，递进遍历
//(3) 若相同，则子串索引向前
//(4) 否则，父串索引向前，子串归位
//(5) 判断sd的末尾指针的值；
//(6) 若相同，则返回锁定的父串索引；否则，失败

int FindStr2(const char *si, const char *sd)
{
    int i = 0, j = 0;
    while (si[i] != '' && sd[j] != '')
    {
        if (si[i + j] == sd[j])
        {
            ++j;      // 子串向前,驱动父串,相提并论
        }
        else 
        {
            i += 1;   // 父串前迈一步
            j = 0;    // 子串前功尽弃
        }
    }
    if (sd[j] == '')
    {
        return i;    // 返回起始点
    }
    else
    {
        return -1;   // 失败
    }
}

//第三种简单方法(第二种的思想)(简称：月亮走我也走)

int FindStr3(const char *si, const char *sd)
{
    int i = 0, j = 0;
    while (si[i] != '' && sd[j] != '')
    {
        if (si[i] == sd[j])
        {
            ++i;   // 父串向前
            ++j;   // 子串向前
        }
        else
        {
            i = i - j + 1;   // 父串前迈一步
            j = 0;       // 子串前功尽弃
        }
    }
    if (sd[j] == '')
    {
        return i - j;   // 从起始处算起
    }
    else
    { 
        return -1;      // 失败
    }
}

//第四种方法

void SubNext(const char *sd, int next[])
{
    next[0] = -1;    
    int i = 0, j = 1;         
    while (sd[j] != '')
    {
        int k = j-1;    
        while (k > 0)
        {
            for (i = 0; i < k; ++i)
            {
                if (sd[i] != sd[j - k + i])    
                {
                     break;
                }
            }
            if (i >= k)
            { 
                break;
            }
            else
            {
                --k;
            }
        }
        next[j] = k;
        ++j;
    }
}

int FindStr4(const char *si, const char *sd, int next[])
{
    int i = 0, j = 0;
    int m = strlen(si), n = strlen(sd);
    while (i < m && j < n)
    {
        if (j == -1 || si[i] == sd[j])
        {
            ++i;
            ++j;
        }
        else
        {
            j = next[j];
        }
    }
    if (sd[j] == '')
    {
        return i - j;
    }
    else
    {
        return -1;
    }
}

//第五种方法

void SubNext_kmp(const char *sd, int next[])
{
    next[0] = -1;    
    int j = 0;
    int k = -1;
    while (sd[j] != '')
    {
        if (k == -1 || sd[k] == sd[j])
        {
            ++j;
            ++k;
            next[j] = k;
        }
        else
        {
            k = next[k];
        }
    }
}

void main()
{
    char str1[] = {"BBC ABCDAB ABCDABCDABDE"};
    char str2[] = {"ABCDABD"};

    int pos1 = FindStr1(str1, str2);
    printf("pos1 :: %d
", pos1);

    int pos2 = FindStr2(str1, str2);
    printf("pos2 :: %d
", pos2);

    int pos3 = FindStr3(str1, str2);
    printf("pos3 :: %d
", pos3);

    int* pNext = (int*)malloc(sizeof(int) * sizeof(str2));
    memset(pNext, 0, sizeof(int) * sizeof(str2));
    SubNext_kmp(str2, pNext);
    for (size_t i = 0; i < strlen(str2); ++i)
    {
        printf("%d ", pNext[i]);
    }
    int pos4 = FindStr4(str1, str2, pNext);
    printf("pos4 :: %d 
", pos4);

    memset(pNext, 0, sizeof(int) * sizeof(str2));
    SubNext_kmp(str2, pNext);
    for (size_t i = 0; i < strlen(str2); ++i)
    {
        printf("%d ", pNext[i]);
    }
    int pos5 = FindStr4(str1, str2, pNext);
    printf("pos5 :: %d 
", pos5);

    free(pNext);

    system("pause");
}
// run out:
/*
pos1 :: 15
pos2 :: 15
pos3 :: 15
-1 0 0 0 0 1 2 pos4 :: 15
-1 0 0 0 0 1 2 pos5 :: 15
请按任意键继续. . .
*/

 以上实现。

 【3】总结

参见大牛的文章《 字符串匹配的KMP算法 》

Good  Good  Study,  Day  Day  Up.

顺序  选择  循环  总结