AtCoder Regular Contest 081

AtCoder Regular Contest 081

C - Make a Rectangle

---

Time limit : 2sec / Memory limit : 256MB

Score : 300 points

Problem Statement

We have N sticks with negligible thickness. The length of the i-th stick is Ai.

Snuke wants to select four different sticks from these sticks and form a rectangle (including a square), using the sticks as its sides. Find the maximum possible area of the rectangle.

Constraints

• 4≤N≤105
• 1≤Ai≤109
• Ai is an integer.

---

Input

Input is given from Standard Input in the following format:

N
A1 A2 ... AN

Output

Print the maximum possible area of the rectangle. If no rectangle can be formed, print 0.

---

Sample Input 1

Copy

6
3 1 2 4 2 1

Sample Output 1

Copy

2

1×2 rectangle can be formed.

---

Sample Input 2

Copy

4
1 2 3 4

Sample Output 2

Copy

0

No rectangle can be formed.

---

Sample Input 3

Copy

10
3 3 3 3 4 4 4 5 5 5

Sample Output 3

Copy

20

---

找两条最大的边就好了，这个内存给的多，随便写都行的

#include <bits/stdc++.h>
using namespace std;
int main()
{
    int n;
    cin>>n;
    set<int>S;
    vector<int>B;
    for(int i=0;i<n;i++)
    {
        int x;
        cin>>x;
        if(S.count(x)){
        S.erase(x);
        B.push_back(x);}
        else
        S.insert(x);
    }
    sort(B.begin(),B.end());
    if((int)B.size()<2){
        printf("0
");
    }
    else
    {
        int x=(int)B.size();
        printf("%lld",1LL*B[x-1]*B[x-2]);
    }
    return 0;
}

D - Coloring Dominoes

---

Time limit : 2sec / Memory limit : 256MB

Score : 400 points

Problem Statement

We have a board with a 2×N grid. Snuke covered the board with N dominoes without overlaps. Here, a domino can cover a 1×2or 2×1 square.

Then, Snuke decided to paint these dominoes using three colors: red, cyan and green. Two dominoes that are adjacent by side should be painted by different colors. Here, it is not always necessary to use all three colors.

Find the number of such ways to paint the dominoes, modulo 1000000007.

The arrangement of the dominoes is given to you as two strings S1 and S2 in the following manner:

• Each domino is represented by a different English letter (lowercase or uppercase).
• The j-th character in Si represents the domino that occupies the square at the i-th row from the top and j-th column from the left.

Constraints

• 1≤N≤52
• |S1|=|S2|=N
• S1 and S2 consist of lowercase and uppercase English letters.
• S1 and S2 represent a valid arrangement of dominoes.

---

Input

Input is given from Standard Input in the following format:

N
S1
S2

Output

Print the number of such ways to paint the dominoes, modulo 1000000007.

---

Sample Input 1

Copy

3
aab
ccb

Sample Output 1

Copy

6

There are six ways as shown below:

---

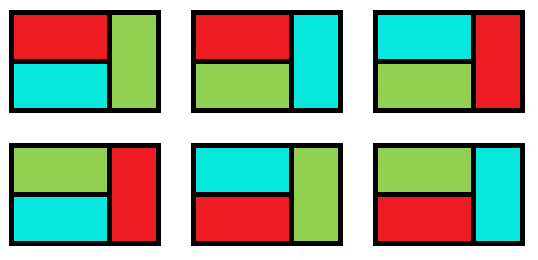
Sample Input 2

Copy

1
Z
Z

Sample Output 2

Copy

3

Note that it is not always necessary to use all the colors.

---

Sample Input 3

Copy

52
RvvttdWIyyPPQFFZZssffEEkkaSSDKqcibbeYrhAljCCGGJppHHn
RLLwwdWIxxNNQUUXXVVMMooBBaggDKqcimmeYrhAljOOTTJuuzzn

Sample Output 3

Copy

958681902

---

依旧随手A，分情况讨论，第一个是特殊的，然后讨论前后就行了，mmp，没有看清题目条件

达成成就，给他们讲明白了这个题、

#include <bits/stdc++.h>
using namespace std;
char s[60];
long long dp[60];
int a[60];
const int MD=1000000007;
int main()
{
    int n;
    scanf("%d",&n);
    int t=0;
    scanf("%s",s+1);
    for(int i=1; i<=n; i++)
        if(s[i]==s[i-1])
            a[t]++;
        else
            a[++t]++;
    if(a[1]==1)dp[1]=3;
    else dp[1]=6;
    for(int i=2; i<=t; i++)
    {
        if(a[i-1]==2)
        {
            if(a[i]==2)
                dp[i]=dp[i-1]*3%MD;
            else if(a[i]==1)
                dp[i]=dp[i-1];
        }
        else if(a[i-1]==1)
        {
            if(a[i]==2||a[i]==1)
            dp[i]=dp[i-1]*2%MD;
        }
    }
    scanf("%s",s+1);
    cout<<dp[t];
    return 0;
}

E - Don't Be a Subsequence

---

Time limit : 2sec / Memory limit : 256MB

Score : 600 points

Problem Statement

A subsequence of a string S is a string that can be obtained by deleting zero or more characters from S without changing the order of the remaining characters. For example, arc, artistic and (an empty string) are all subsequences of artistic; abc and ci are not.

You are given a string A consisting of lowercase English letters. Find the shortest string among the strings consisting of lowercase English letters that are not subsequences of A. If there are more than one such string, find the lexicographically smallest one among them.

Constraints

• 1≤|A|≤2×105
• A consists of lowercase English letters.

---

Input

Input is given from Standard Input in the following format:

A

Output

Print the lexicographically smallest string among the shortest strings consisting of lowercase English letters that are not subsequences of A.

---

Sample Input 1

Copy

atcoderregularcontest

Sample Output 1

Copy

b

The string atcoderregularcontest contains a as a subsequence, but not b.

---

Sample Input 2

Copy

abcdefghijklmnopqrstuvwxyz

Sample Output 2

Copy

aa

---

Sample Input 3

Copy

frqnvhydscshfcgdemurlfrutcpzhopfotpifgepnqjxupnskapziurswqazdwnwbgdhyktfyhqqxpoidfhjdakoxraiedxskywuepzfniuyskxiyjpjlxuqnfgmnjcvtlpnclfkpervxmdbvrbrdn

Sample Output 3

Copy

aca

---

E就比较难了，要你找一个字符串是题目中没有出现的最小子串

窝还想着要字典树什么的，PP的做法是反向建图最短路

我看的别人的代码基本就是贪心的暴力，处理的很巧妙

#include<bits/stdc++.h>
using namespace std;
const int N=200005;
int n,a[27],f[N],g[N],dp[N];
char s[N];
int main()
{
    scanf("%s",s+1);
    n=strlen(s+1);
    f[n+1]=n+2;
    g[n+1]=1;
    dp[n+1]=1;
    for (int i=1; i<=26; i++)
    {
        a[i]=n+1;
    }
    for (int i=n; i>=1; i--)
    {
        a[s[i]-'a'+1]=i;
        int t=1;
        for (int j=2; j<=26; j++)
        if (dp[a[j]+1]<dp[a[t]+1])t=j;
        dp[i]=dp[a[t]+1]+1;
        f[i]=a[t];
        g[i]=t;
    }
    int now=1;
    while(now<=n+1)
    {
        putchar(g[now]+'a'-1);
        now=f[now]+1;
    }
    return 0;
}