1.问题动机
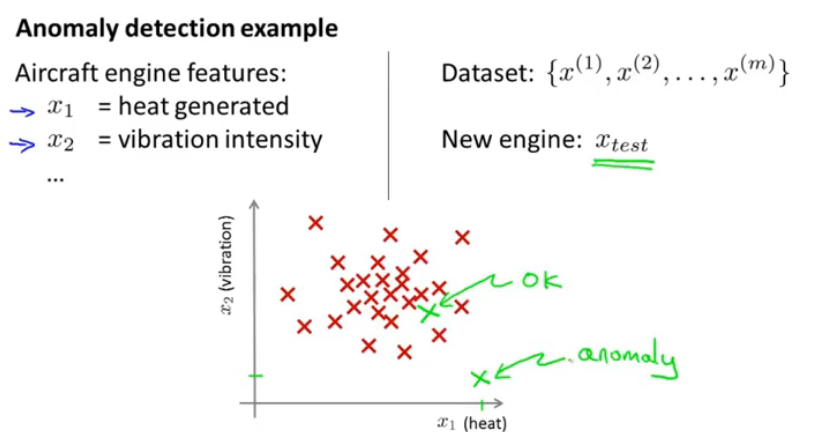
图1.飞机发动机检测例子
对飞机引擎的例子,如果选取了两个特征x1热量产生度,x2震动强度。并得到如下的图,如果有一个新的引擎来检测其是否正常,x_test,那么此时如果点落在和其他点正常内,那么就显示是正常,不需要进一步的检测,但是如果在右下角绿色的,那么就是异常的,需要进一步地检测。
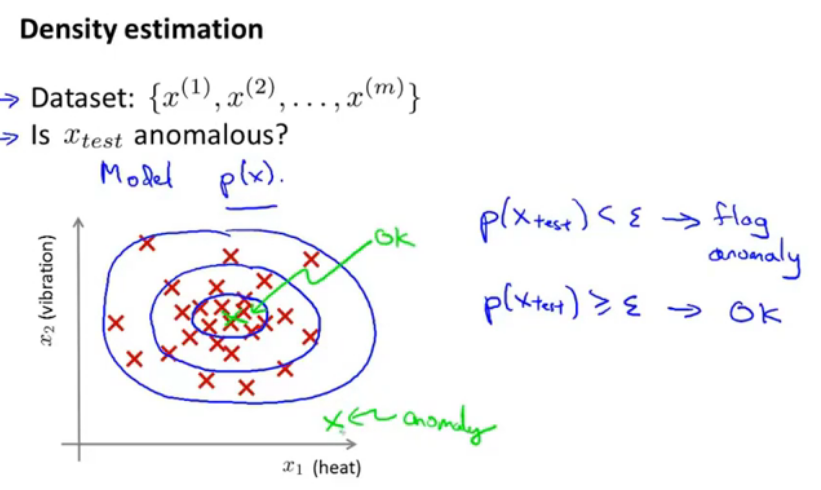
图1.密度检测
更一般地建立模型,当x_test输入时,若概率<阈值ε,那么就被设置为异常;否则设置为正常。如图来看,中心部分的概率大,四周部分概率小。
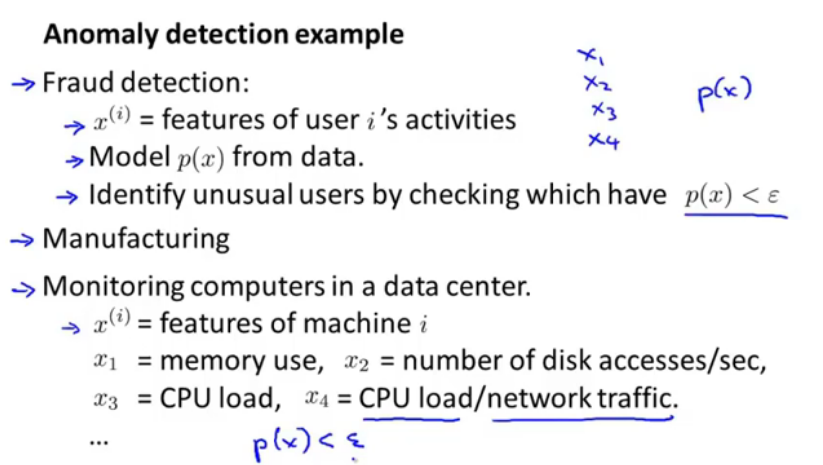
图2.异常检测的应用
异常检测最常见的应用是进行,用户欺诈检测,对用户的模型作为向量,从数据中建立模型,异常用户为:p(x)<ε。还有在工业生产,检测计算机中心。
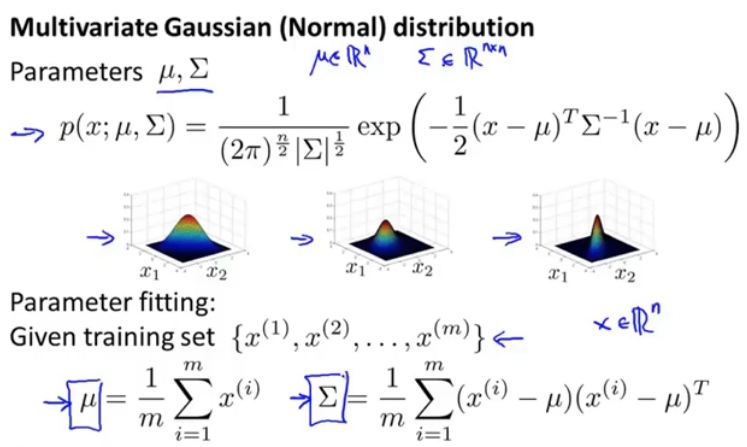
2.高斯分布/正态分布
其中μ是均值,σ是方差,可以使用公式来计算。曲线特点:当σ越小时,曲线越瘦高;当σ越大时,曲线越胖矮。并且根据概率的性质,曲线下方面积为1。
3.算法

图3.密度估计问题
对一个无标记的训练集来说,建立的模型为如上式,是一个独立假设问题,假设x_i均服从正态分布并且使独立的,那么p(x)就是这个密度估计模型,写成了阶乘的形式。(也是符合高斯分布的,当其处于均值附近,那么p就对应比较大,是符合刚刚讲的检测结果,如果p(x)<σ,那么就是异常的,不符合大部分点的分布。)

图4.异常检测算法
这就是所谓的异常检测算法,不就是求训练集的高斯分布参数,有新的样本来时,观察其是否分布在均值附近了。最终结果,如果p(x)<σ,那么就是异常的。
注意:这里不是对一个向量x,而是针对向量中每个分量,即每个特征值!,都有那么一个高斯分布,并且整个样本的决定是通过连乘。
4.开发和评估异常检测系统

图5.数值评估的重要性
当进行一个学习算法时,当有一个方法来进行评估,那么此时是更容易决策的。
假设现在有一些标记数据,y=1表示是异常的,在训练集中假设全都是正常样本,不包括异常样本,并且有验证集和训练集。

图6.发动机引擎例子
假设数据集一共包括10000个正常引擎数据和20个一场引擎数据,好的数据集分法是:
训练集中有6000个正常引擎数据,交叉验证集中2000个正常,10个异常,测试集中2000个正常,10个异常。通常交叉验证机和测试集的数据是不一样的,也不应该是一样的。
下一种分法是不好的分法,但通常有人这么做,就是将交叉验证集和测试集中的数据完全一样,这是不可取的。

图7.算法评估
通过在训练集上训练出模型,当p(x)<ε时被判断为异常点,反正则正常;
那么如何去评估这个算法呢?由于这个问题数据集明显是偏斜的,所以使用以下:
查准率和查全率,F_1公式;
或者也可以使用在交叉验证集上设置阈值ε来计算,这个和公式判断异常或正常中的ε是相同的。通过设置很多ε,并且在交叉验证集上测试,并选取一个让F_1公式最高的ε。(并且使用这个来决策,也可以决定哪个特征应该被选择,哪个不被选择。)
5.异常检测VS监督学习
那么既然对于有标签的数据,为什么使用异常检测而不是直接训练一个监督学习的模型呢?

图8.异常检测与监督学习
异常检测的数据集特征:通常都是负例,只有很少的部分是正例(0-20是比较常见的)。
有很多种不同类型的异常,并且很难从正例中去找出算法来学习其特征(比如飞机发动机引擎出故障的原因),并且下次出现的异常很有可能从来没见过。
监督学习的数据集特征:有大量的正例和负例。
能够有足够多的正例去让算法获取特征,将来出来的样例可能和之前在训练集中出现的类似。
比如对于垃圾邮件分类,虽然很有可能下一次出现的并不和之前训练集中相同,但是因为可以获取足够多的垃圾邮件的数据,所以通常使用监督学习的方法来进行垃圾邮件分类。

图9.问题应用
对于异常检测:缺陷检测、工业生产、数据中心监督机器。(关键点是这些缺陷点的数据够不够多,比如在工业生产中,如果缺陷数据够多,那么也可也建立监督模型。)
监督学习:垃圾邮件分类、天气预测、癌症分类。
6.选择要使用的特征
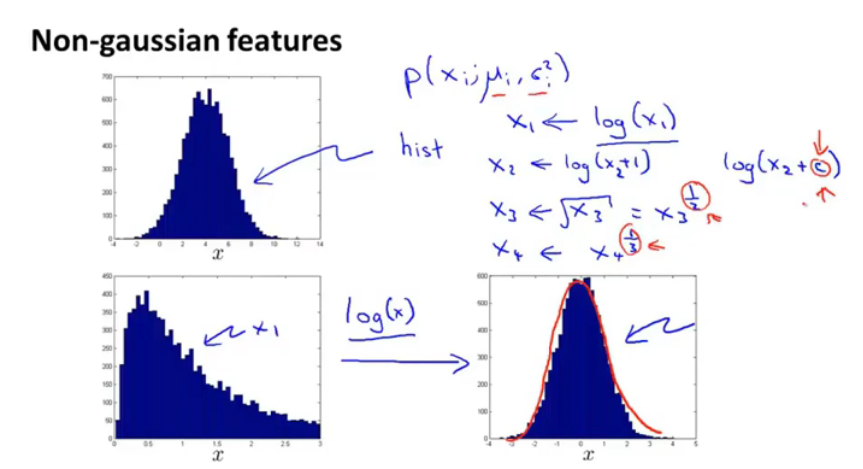
图10.不是高斯分布的特征
图中1是很类似于高斯分布的,所以这样的特征是很乐意加进来的,但是像图中2,就需要进行一下转换来使其尽量符合高斯分布。
比如:取logx、或者log(x+c)、取根号。
图中红圈标出来的均是可调整参数,都是为了让特征数据分布更趋近于高斯分布。
关于异常算法的误差检测,如果表现不好,那么就考虑那个未能正常分类的异常数据,去观察它,并且判断能否新建一个特征x_2来区别这个异常数据以改进算法。
那么如何进行特征选择呢?

图11.在数据中心的电脑检测例子
Ng会选择那些数值及不是很大,也不是很小的特征。
比如对x_3和x_4,分别表示CPU负载和网络流量,发现基本是线性关系,但是当发现网络流量上升很大时,CPU却上升不明显,是因为CPU做了很多工作卡死了。
在这种情况下,要想检测出异常,就可以新建一个特征x_5或者x_6.
7.多变量高斯分布
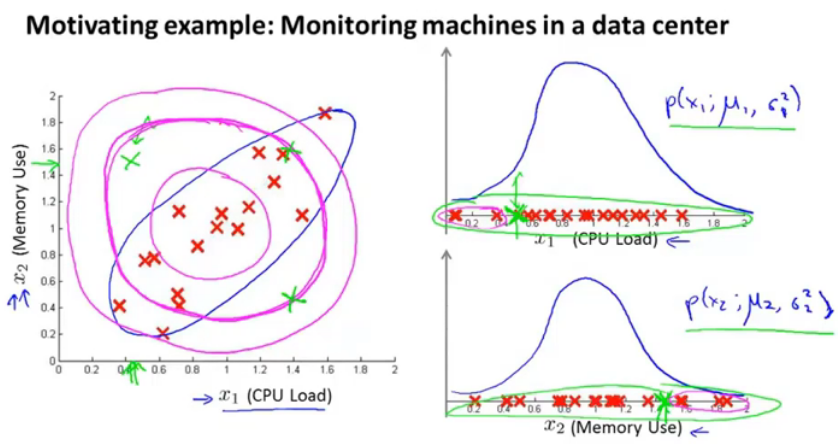
图12.单变量高斯分布判断存在隐患
如果有一个点是图中1左上角的绿色点,那么从图中1来看其是异常点,但是对应对每个特征建模的高斯分布,每个分布的P都比较高,所以最终得出的乘积也比较高,因此就出现了问题。单个变量进行高斯分布建模,不好。
第二层洋红色圈即表示,出现在这一范围内很大可能被表示为正常数据。
所以接下来介绍多变量高斯分布建模,避免类似的问题出现。
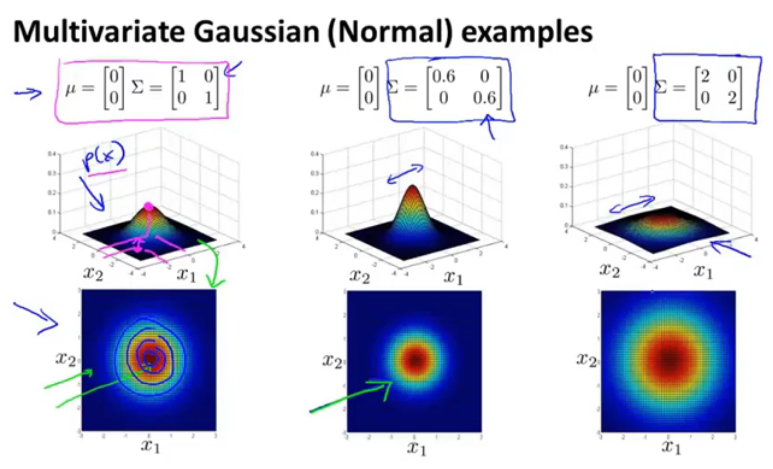
图13.多变量高斯分布可视化
这里的Σ矩阵就相当于方差,它的行列式即方差,那么和一维的是类似的。
当Σ较小时,较高瘦;当Σ较大时,较胖矮。
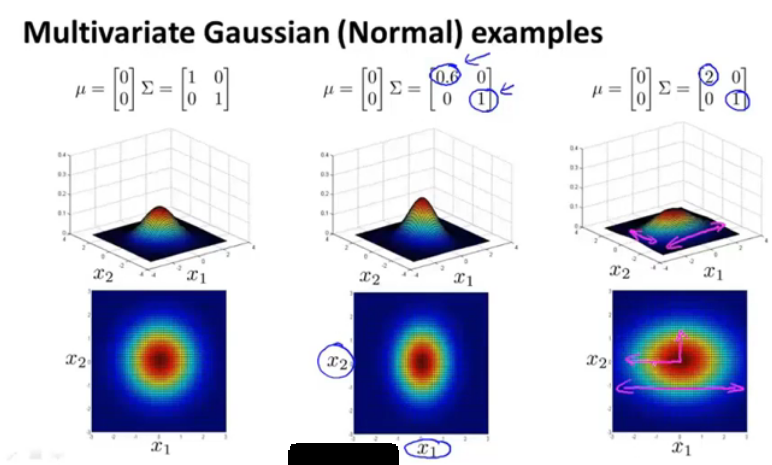
图14.Σ矩阵变化的影响
对于协方差矩阵Σ的行列式,对图中2,当第一行的方方差减小时,明显图中x_1对应的是在变小。
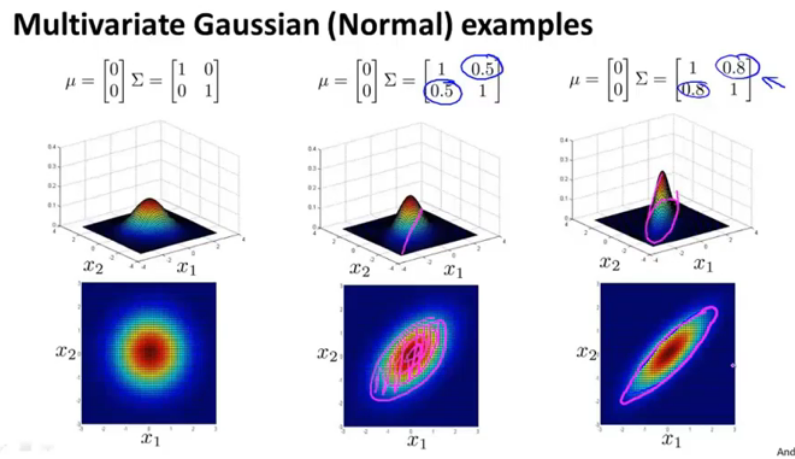
图15.多变量高斯分布的例子
当改变Σ行列式的非对角线上的元素时,对应的形状也会发生改变,这样就对应了开头的例子,可以解决对应的问题,
8.使用多变量高斯分布的异常检测
图16.多变量高斯分布公式
当给出一个训练集时,可以计算出参数μ和Σ。(这里不是计算出每个特征对应的参数,而是每一个测试数据都是整个向量代入的。)

图17.多变量高斯分布模型
首先通过μ和协方差矩阵Σ,拟合出一个模型, 然后再给出一个新的样本,计算p(x)。
在图中,距离椭圆中心越近表示概率越高,反之绿色的点此时就会被判定为异常。

图18.多变量与原始模型的关系
原始的模型不能表示变量与变量之间的关系,而且它们的投影圆的对称轴都是与坐标轴垂直的。
而在多变量正态分布中,有协方差矩阵,但是当协方差矩阵为对角阵时,就会退化为原始模型(不能表示不同变量之间的关系了)。
原始模型只是高斯分布的一种特殊情况。

图19.原始模型VS多变量高斯模型
1.当你想通过特征的组合来判断异常时,比如之前举的例子中,x_3=x_1/x_2=CPU负载/内存,原始模型需要手动地去选择特征组合,
而多变量模型可以自动地表示特征与特征之间的关系,因为它有协方差矩阵了。监测到异常就将其标记。
2.原始模型适合n较大的时候,即n=100,000,之类,计算量较小;对于多变量来说,由于需要计算逆矩阵,计算量很大,对应于n较小的情况。
3.原始模型中对训练集m很小也是可以使用的;多变量中,需要满足两个条件m>n,m要大于n,比如说m>10n,并且必须是可逆的。
不可逆的情况是什么呢?需要用到线代,不可逆也就是|Σ|=0,协方差行列式=0,通过初等行列变换,可以让一行全为0,那么矩阵就是不可逆的,如x_1=x_2,x_3=x_4+x_5.这样的情况