1.无监督学习概述
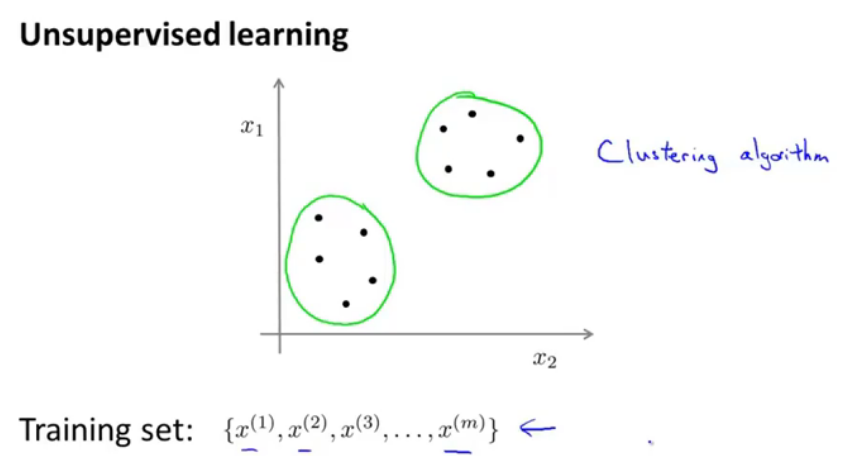
图1.无监督学习
有监督学习中,数据是有标签的,而无监督学习中的训练集是没有标签的,比如聚类算法。
2.k-means算法
k-means算法应用是十分广泛的聚类方法,它包括两个过程,首先是选取聚类中心,然后遍历每一个点,决定其属于哪个类;第二步是移动聚类中心点,根据刚才的聚类情况将聚类中心点移动,下面三个图很好地说明了这个过程:
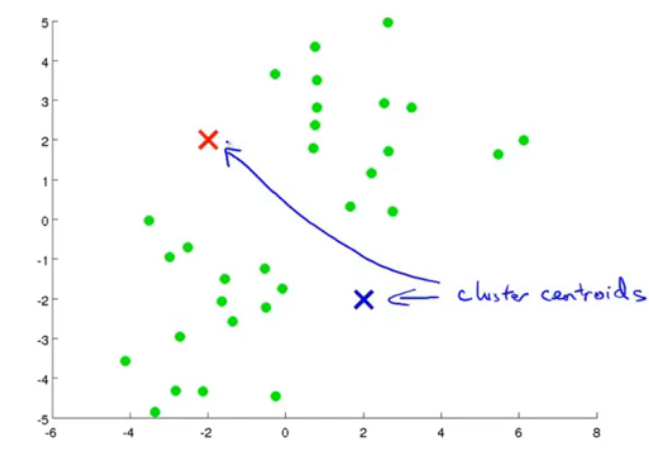
图2.初始化,并且计算距离。
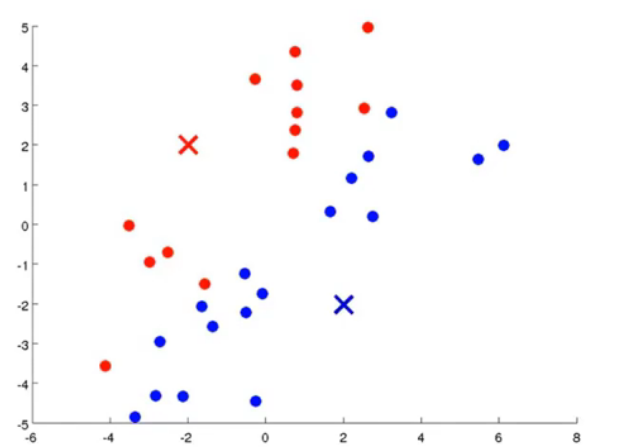
图3.计算距离后
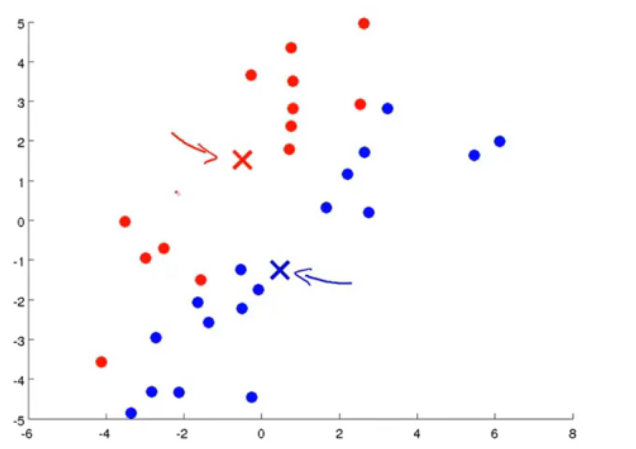
图4.根据最小化均方误差移动聚类中心点
根据新的聚类中心点,再次重复这个过程,

图5.迭代之后最终结果
迭代之后最终结果,就算再运行k-means聚类算法,聚类中心点也不会改变了,

图6.k-means算法输入
输入包括k,之后会讲解如何选择k,训练集,x(i)是n维的,不是n+1维,通常舍去x_0=1项。

图7.k-means算法过程
K是指一共分为几簇,k是指每个聚类中心。
首先随机初始化k各聚类中心点,循环以下过程:
1.将m个样本点遍历,分到k个聚类中心中;
2.根据各个簇中的点到聚类中心点的距离并取均值。
对于聚类结果中,没有点的簇,通常是直接删去,那么K就变成了K-1簇。
3.优化目标

图8.k-means优化目标
就是最小化代价函数,也叫失真代价函数。优化目标就是使点到聚类中心的平均距离最小。
4.随机初始化
这节会讲如何避开局部最优。
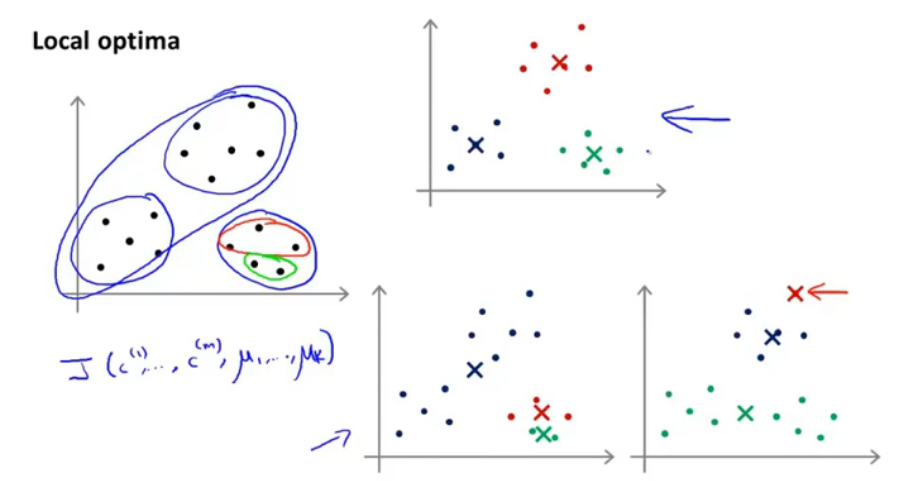
图9.局部最优化情况
如图就是局部最优化情况,两个类被分成了一个簇,一个簇被分开成了两份,这是不好的,是因为聚类中心店的初始化的问题。解决办法就是初始化多次,并且运行多次k-means聚类算法,得到结果,保证得到一个足够好的结果。

图10.运行局部最优化算法
随机初始化,重复k-means算法100次,通常是在50-1000之间,运行结束后,选取一个失真函数最小的聚类结果。
随机初始化的情况,适用于K在2-10之间,多次随机初始化会比较好的得到正确的聚类结果,但是当不在此区间内,聚类结果并不会有很大的改善,K很大时一次聚类结果即可。
5.选择簇的数量
目前来说,还都是通过可视化的方法手动选择的。
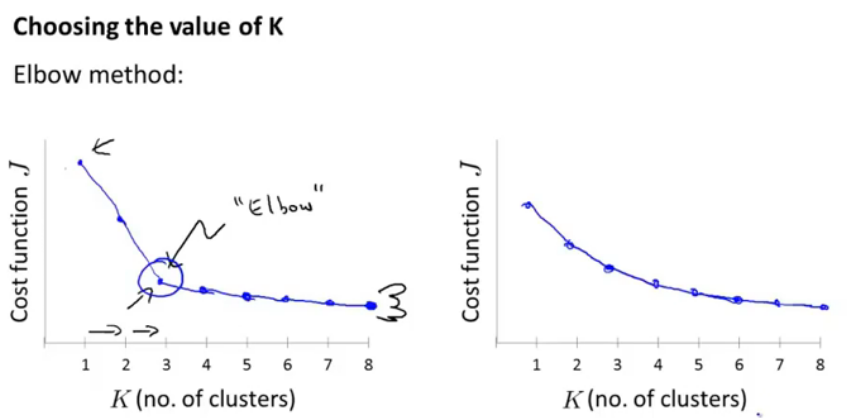
图11.如何选择聚类K的值
选择K个聚类的值,并以损失函数为纵轴来判断,肘形函数,但是有时会像有部,是平滑的,也不好确定最终分为几类,所以这个肘形曲线并不能成为好的判断方法。
但是最终的应用结果会告诉你应该分为几类。
2020-4-13更新————————
1.k-means继续学习
看了上面之前的笔记,就发现,学习还停留在概念上面,没有具体的数学公式和实现代码,这就比较飘了。
https://blog.csdn.net/huangfei711/article/details/78480078 这个讲的还是挺通俗易懂的,原来在计算过程中会出现虚拟的中心点啊,直到分类结果没有什么变化就认为是收敛了。
首先随机选取K个点,然后计算所有其他点到这两个点的距离,根据小的确定分类,然后在各个类中再选出中心点,计算中心点是通过x/y轴的均值计算出一个可能是虚拟的点的坐标(重心),计算所有距离将点再分类,然后这样循环下去。
https://blog.csdn.net/sinat_26917383/article/details/70240628,给出了使用sklearn实现的例子:
import numpy as np from sklearn.cluster import KMeans data = np.random.rand(100, 3) #生成一个随机数据,样本大小为100, 特征数为3 #假如我要构造一个聚类数为3的聚类器 estimator = KMeans(n_clusters=3)#构造聚类器 estimator.fit(data)#聚类 label_pred = estimator.labels_ #获取聚类标签 centroids = estimator.cluster_centers_ #获取聚类中心 inertia = estimator.inertia_ # 获取聚类准则的总和 #输出: >>> centroids array([[0.42927216, 0.57043035, 0.19739574], [0.76233694, 0.46150249, 0.69253087], [0.25571954, 0.41477208, 0.79997927]]) >>> inertia 13.015626730491624