归并排序学习

https://blog.csdn.net/qq_25827845/article/details/70994874

1.总体思想，就是分治

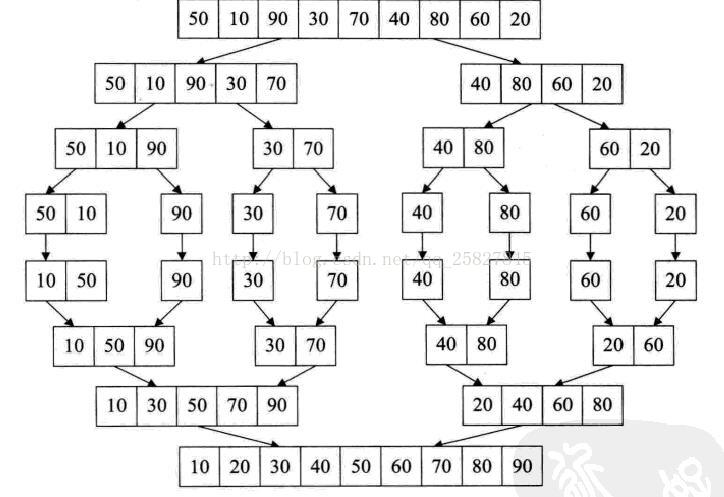
 关于时间复杂度我一直都很迷，但是看了实现之后，就明白了，merge的时间复杂度是O(n)因为，有O(logn)层吧，所以时间复杂度就是两者相乘。

#还是不理解，抽象，先死记一下。

因为在merge的时候需要创建一个新数组来保存有序的排列，所以空间复杂度为O(n)。

import java.util.Arrays;
 
public class Test {  
    // 归并排序的实现  
    public static void main(String[] args) {  
  
        int[] nums = { 2, 7, 8, 3, 1, 6, 9, 0, 5, 4, -3};  
        System.out.println(Arrays.toString(nums));  
        sort(nums, 0, nums.length-1);  
        System.out.println(Arrays.toString(nums));  
    }
    
    /** 
     * 归并排序 
     * 简介:将两个（或两个以上）有序表合并成一个新的有序表 即把待排序序列分为若干个子序列，
     *     每个子序列是有序的。然后再把有序子序列合并为整体有序序列 
     * 时间复杂度为O(nlogn) 
     * 稳定排序方式 
     * @param nums 待排序数组 
     * @return 输出有序数组 
     */  
    public static int[] sort(int[] nums, int low, int high){
        int mid = (low+high)/2;
        if(low<high){
            // 处理左边
            sort(nums, low, mid);
            // 处理右边
            sort(nums, mid+1, high);
            // 左右归并
            merge(nums, low, mid, high);
        }
        return nums;
    }
    private static void merge(int[] nums, int low, int mid, int high) {
    // 定义一个辅助数组，所以该算法的空间复杂度为O（n）
        int[] temp = new int[high-low+1];
        int i = low;
        int j = mid+1;
        int k = 0;
        // 找出较小值元素放入temp数组中
        while(i<=mid && j<=high){
            if(nums[i]<=nums[j])
                temp[k++] = nums[i++];
            else
                temp[k++] = nums[j++];
        }
        // 处理较长部分
        while(i<=mid){
            temp[k++] = nums[i++];
        }
        while(j<=high){
            temp[k++] = nums[j++];
        }
        // 使用temp中的元素覆盖nums中元素
        for (int k2 = 0; k2 < temp.length; k2++) {
            nums[k2+low] = temp[k2];
        }
    }
}