今年2018年的杭电计算机学院复试题的第一道题目和第二道题目虽然题目比较长,但是比较简单和基础,这里就不详细说明了。
第三道题目是用到数据结构中的知识。
题目如下:
瓜农王大爷去年种西瓜赚了不少钱。看到收入不错,今年他又重新开辟了n个西瓜地。
为了能给他的n个西瓜地顺利的浇上水,对于每个西瓜地他可以选择在本地打井,也可以修管道从另一个瓜地(这个瓜地可能打了井;也可能没打井,他的水也是从其他瓜地引来的)将水引过来。
当然打井和修管道的费用有差别。已知在第i个西瓜地打井需要耗费wi元,在第i、j个西瓜地之间修管道需要耗费pi,j元。
现在的问题是:王大爷要想使所有瓜地都被浇上水,至少需要花费多少钱(打井与修管道的费用和)?
由于瓜地较多,王大爷无法选择在哪些(个)瓜地打井,哪些西瓜地之间修管道。
请你编程帮王大爷做出决策,求出最小费用。
输入格式
第1行,一个正整数n,代表西瓜地的数量。
以下n行,依次给出整数w1..wn(每块西瓜地的打井费用)。
紧接着是一个n*n的整数矩阵,矩阵的第i行第j列的数代表pi,j(两块西瓜地之间建立管道的费用)。每行的两个数之间有一个空格隔开。
6
5
4
4
3
1
20
0 2 2 2 9 9
2 0 3 3 9 9
2 3 0 4 9 9
2 3 4 0 9 9
9 9 9 9 0 9
9 9 9 9 9 0
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
样例说明
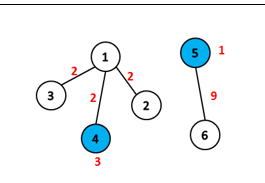
在第4个瓜地打井(费用为3),然后将第2,3,4个瓜地与第1个瓜地间修管道(费用分别是2,2,2),这样水可以经过管道从4流向1,然后经1再流向2和3;
在第5个瓜地打井(费用为1),5和6之间修管道(费用为9)。
这样一共打了2口井,修了4条管道,能给所有的6个瓜地浇水,费用是:3+2+2+2+1+9=19。
数据规模和约定
对于所有数据,1<=N<=300,1<=wi<=100000;pi,i=0,1<=pi,j=pj,i<=100000。
算法思路
应用贪婪算法,先在打井费用最便宜的地打井,用已有水源的地更新没有水源的地(判断两者之间是否适合挖管道),若所有地都有水源,算法结束,否则,打下一口井
源程序
#include <stdio.h> int flg[1000]; /*保存打井或者挖管道信息,0挖管道,1打井 */ int barr[1000][1000]; int arr[1000]; void update(int *st, int n); int find(int *arr, int n, int last)/*找出打井费用最低的地*/ { int i; int min = arr[1]; int rt = 1; for (i = 2; i < n + 1; i++) if (arr[i] < min && arr[i] > last) { min = arr[i]; rt = i; } return rt; } int check(int *a, int n)/*检查当前所有土地是否都有水源*/ { int i; for (i = 1; i < n + 1; i++) { if (a[i] > 0) ; else break; } if (i == n + 1) return 0; else return 1; } int main(void) { int i, j, k; int n; if (freopen("water.in", "r", stdin) == NULL) return -1; scanf("%d", &n); int st[n + 1]; /*保存有水源的地打井或者挖管道的费用 */ for (i = 1; i < n + 1; i++) scanf("%d", &arr[i]); for (i = 1; i < n + 1; i++) for (j = 1; j < n + 1; j++) scanf("%d", &barr[i][j]); for (i = 0; i < n + 1; i++) { st[i] = 0; flg[i] = 0; } k = find(arr, n, 0); while (check(st, n) != 0) { if (st[k] == 0) { st[k] = arr[k]; flg[k] = 1; printf("第%d块地打井 ", k); } for (i = 1; i < n + 1; i++) { if (st[i] > 0) continue; int flag = 1; if (i == k || barr[i][k] > arr[i]) continue; else { for (j = 1; j < n + 1; j++) { if (i != j && barr[i][j] < barr[i][k] && j != k) { flag = 0; break; } } if (flag == 1 && st[i] == 0) { st[i] = barr[i][k]; printf ("第%d块地与第%d块地挖管道 ", i, k); } } } update(st, n); k = find(arr, n, st[k]); } for (i = 1; i < n + 1; i++) printf("%d ", st[i]); printf(" "); return 0; } /*当i块地接通水源以后别的地可以通过与挖它管道接通水源 * 本函数作用是确定没有水源的地与i块地之间的管道*/ void update(int *st, int n) { int i, j, k, l; for (l = 1; l < n + 1; l++) { if (st[l] > 0 && flg[l] == 0) k = l; else continue; for (i = 1; i < n + 1; i++) { if (st[i] > 0 && flg[i] == 1) /*flg[i]=1,打井的地,费用信息不能更新 */ continue; int flag = 1; /*跳过与第i块间管道费用比打井贵的地 */ if (i == k || barr[i][k] > arr[i]) continue; else { /**/ for (j = 1; j < n + 1; j++) { if (i != j && barr[i][j] < barr[i][k] && j != k) { flag = 0; break; } } if (flag == 1 && st[i] == 0 && flg[i] == 0) { st[i] = barr[i][k]; printf ("第%d块地与第%d块地挖管道 ", i, k); } } } } }
参考博客:https://blog.csdn.net/dmgy110/article/details/50637401