一、母函数
1.定义:对于序列a0,a1,a2,…构造一函数: 
称函数G(x)是序列a0,a1,a2,…的母函数。
2.举例
1)几种砝码(1g,2g,3g,4g的砝码各一个)组合称重的情况
考虑构造母函数。 如果用x的指数表示称出的重量,则: 1个1克的砝码可以用函数1+x表示, 1个2克的砝码可以用函数1+x2表示, 1个3克的砝码可以用函数1+x3表示, 1个4克的砝码可以用函数1+x4表示。
几种砝码的组合可以称重的情况,可以用以上几个函数的乘积表示:
(1+x)(1+x2)(1+x3)(1+x4) =(1+x+x2+x3)(1+x3+x4+x7) =1+x+x2+2x3+2x4+2x5+2x6+2x7+x8+x9+x10
{从上面的函数可以知道,可以称出1g-10g,指数便是可以称出的重量,相应的系数便是能称出该重量的方案个数}
2)求用1分、2分、3分的邮票贴出不同数值的方案数
因邮票允许重复,所以母函数为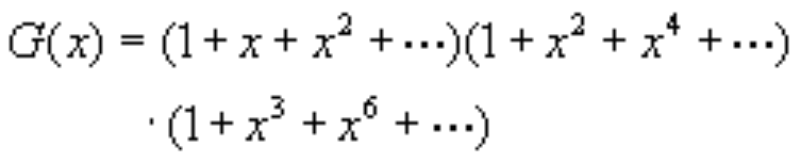
以展开后的x4为例,其系数为4,即4拆分成1、2、3之和的拆分数为4,即 : 4=1+1+1+1=1+1+2=1+3=2+2
3)整数拆分
所谓整数拆分即把整数分解成若干整数的和,相当于把n个无区别的球放到n个无标志的盒子,盒子允许空着,也允许放多于一个球。
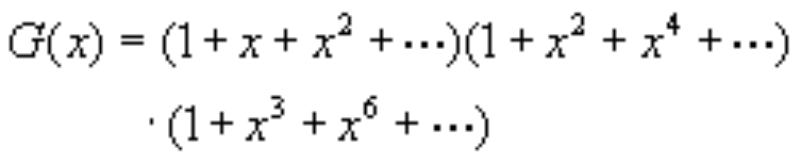
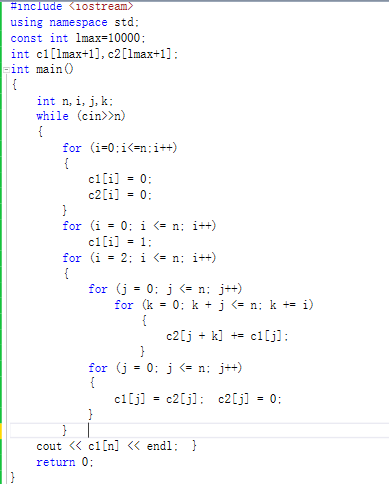
3.实现母函数的应用(关键是多项式展开)
整数拆分为例: