n<=10000的树,节点有初始石头数<=1000,进行这样的游戏:两人轮流行动,我先手,每次可以选一个节点(≠1)把不超过m<=1000个石头移到父亲,最后所有石头都在节点1,没法行动的算输。有T<=10000次修改操作,把某点初始石头数修改,求每次修改后能否先手胜。
突然发现博弈全忘光了。。
首先看:
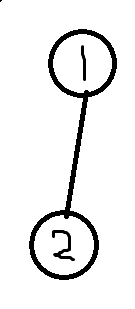
最简单的一种情况,可以用SG函数表示二号点的情况。可以打表或手推或显然得出SG值:0 1 2 …… m 0 1 2 …… m …… SG(i)=i%(m+1)。
接着看并联情况:
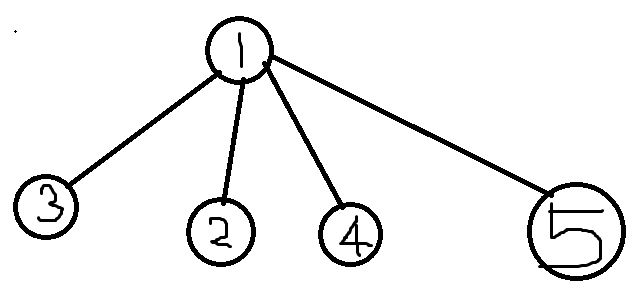
这就是几个互不影响的游戏的组合,用SG定理,把SG值异或起来即可。
重点来了!串联的情况!
http://blog.csdn.net/longshuai0821/article/details/7793043 贴个阶梯博弈先

先不看四号和五号。如果在二号先手就必胜了,那么对手肯定不会甘于在二号点移动而是跑去三号点试图改变局面,但这是徒劳的:我可以把他移过来2号点的东西全部丢到一号点,从而毫不影响先手胜的局面,也就是三号对答案毫无影响。现在看四不看五,由于三号对答案无影响,四号应该发挥积极作用,也就是如果从四号拿了一些到三号,是会影响结果的,这等价于从四号点拿了一些石头丢掉了!因为三号点是没用点,有多少石头都无所谓!也就是说四号点和二号点两个互不影响地构成了这个游戏且规则相同。最后看五号点,如果对手把五号点丢给四号,那么我也可以把丢到四号的那些石头丢给三号。
综上,与根距离为偶数的点都是废点。所以只需要记录并更新距离是奇数的点SG值即可。

1 #include<stdio.h> 2 #include<string.h> 3 #include<algorithm> 4 #include<stdlib.h> 5 #include<iostream> 6 using namespace std; 7 8 int n,t,m; 9 #define maxn 10011 10 struct Edge{int to,next;}edge[maxn<<1];int first[maxn],le=2; 11 void in(int x,int y) {Edge &e=edge[le];e.to=y;e.next=first[x];first[x]=le++;} 12 void insert(int x,int y) {in(x,y);in(y,x);} 13 int val[maxn],dep[maxn],ans; 14 void dfs(int x,int fa) 15 { 16 dep[x]=dep[fa]+1; 17 if (dep[x]&1) ans^=val[x]; 18 for (int i=first[x];i;i=edge[i].next) 19 { 20 const Edge &e=edge[i];if (e.to==fa) continue; 21 dfs(e.to,x); 22 } 23 } 24 int calc(int x) {return x%(m+1);} 25 int main() 26 { 27 scanf("%d%d%d",&n,&t,&m); 28 int x,y; 29 for (int i=2;i<=n;i++) 30 { 31 scanf("%d%d",&x,&y); 32 insert(x,i); 33 val[i]=calc(y); 34 } 35 dep[0]=-1;ans=0;dfs(1,0); 36 for (int i=1;i<=t;i++) 37 { 38 scanf("%d%d",&x,&y); 39 if (dep[x]&1) 40 { 41 ans^=val[x]; 42 val[x]=calc(y); 43 ans^=val[x]; 44 } 45 printf(ans?"Yes ":"No "); 46 } 47 return 0; 48 }
