1138 B
题意
给你两个01串 (a,b) ,现在要选择 (n/2) 个 (i) 组成一个集合 (S) ,使得 (sum_{iin S}a[i]=sum_{j∉S}b[j]) 。
((2le nle 1500))
Examples
inputCopy
4
0011
0101
output
1 4
input
6
000000
111111
output
-1
input
4
0011
1100
output
4 3
input
8
00100101
01111100
output
1 2 3 6
解
设 ((1,0)) 总个数为 (A) , ((0,1)) 总个数为 (B) , ((0,0)) 总个数为 (C) , ((1,1)) 总个数为 (D) , (iin S) 且 ((a[i],b[i])=(1,0)) 个数为 (x) , (iin S) 且 ((a[i],b[i])=(0,1)) 个数为 (y) , (iin S) 且 ((a[i],b[i])=(0,0)) 个数为 (w), (iin S) 且 ((a[i],b[i])=(1,1)) 个数为 (z) 。
有: (x+z=B-y+D-z)
得: (x+y+2z=B+D)
然后只要枚举 (x,y) ,就能求出 (z,w) 。
1138 F
题意
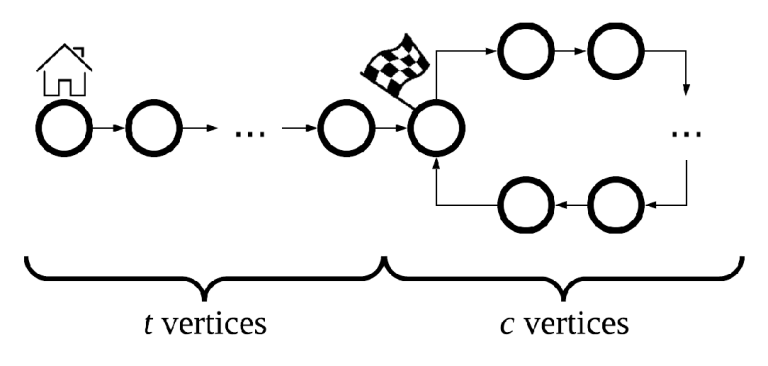
给你一条链,一端连着一个环(全部是有向边),一开始所有人(总共10人,编号 (in [0,9]) )都在最左端的节点,你可以进行最多 (3*n) 次操作,每次可以将若干个人向前移动一步,要你通过交互模拟出所有人到达目的地(旗子处,链和环的交点处)的过程。
每次交互,如果你要移动一步,输出next a1 a2 a3 ,a数组表示要移动的人。如果你能断定所有人已到达目的地,输出done。
每次询问后评测机会返回当前10个人被分成几块。
Example
input
2 05 12346789
3 246789 135 0
3 246789 0 135
3 246789 0 135
2 135 0246789
1 0123456789
output
next 0 5
next 0 1 3
next 2 3 0 1 4 5 6 7 8 9
next 9 8 7 6 5 4 3 2 1 0
next 0 1 3 5
next 1 3 5
done
解
有一种算法叫floyd判环(与 (n^3) floyd最短路算法没什么联系)
具体操作方式:任取两个人 (a,b) ,重复执行:
- 将 (a,b) 向前移动一步;
- 将 (b) 向前移动一步。
直到 (a,b) 相遇。
此时 (a,b) 一定在环上。
然后重复执行:
- 将所有人向前移动一步。
直到所有人相遇。
此时所有人一定在那个目的地节点上。
具体证明列一个方程模拟一下。