论文信息
论文标题:Siamese Attribute-missing Graph Auto-encoder
论文作者:Wenxuan Tu, Sihang Zhou, Yue Liu, Xinwang Liu
论文来源:2021,arXiv
论文地址:download
论文代码:download
1 Introduction
属性缺失:
-
- 1)the absence of particular attributes;
- 2)the absence of all the attributes of specific nodes.
2 Method
总体框架:
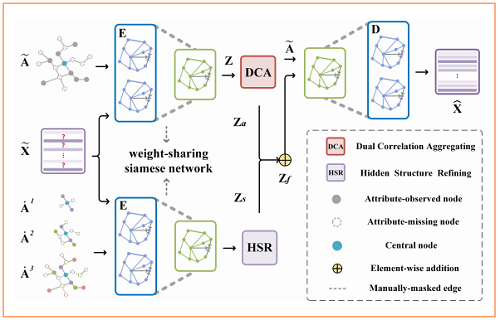
两个主要模块:
-
- a dual correlation aggregating (DCA) module
- a hidden structure refining (HSR) module
2.1 Notations
-
- 属性缺失节点集:$\mathcal{V}^{m}= \left\{v_{1}^{m}, v_{2}^{m}, \ldots, v_{N_{m}}^{m}\right\}$
- 属性完整节点集:$\mathcal{V}^{o}=\left\{v_{1}^{o}, v_{2}^{o}, \ldots, v_{N_{o}}^{o}\right\}$
对于属性缺失的节点集,对其属性 $0$ 填充补齐,得到 $\widetilde{\mathbf{X}} \in \mathbb{R}^{N \times D}$ 。
引入高阶相邻信息 $\mathcal{A}=\left\{\mathbf{A}^{1}, \mathbf{A}^{2}, \ldots, \mathbf{A}^{H}\right\}$,其中 $\mathbf{A}^{h}=\mathbf{A}^{1} \mathbf{A}^{(h-1)}$ 。在训练过程中,我们手动屏蔽了多阶相邻矩阵上的部分连接,以促进网络学习 。因此 $\mathcal{A}$ 定义为 $\dot{\mathcal{A}}=\left\{\dot{\mathbf{A}}^{1}, \dot{\mathbf{A}}^{2}, \ldots, \dot{\mathbf{A}}^{H}\right\}$ 。
2.2 Structure-attribute Mutual Enhancement
Encoder
$\mathbf{Z}^{(l)}=\sigma\left(\widetilde{\mathbf{A}} \mathbf{Z}^{(l-1)} \mathbf{W}^{(l)}\right)$
特别地,我们在编码器后引入了一个额外的操作,如下:
$\mathbf{Z}_{a}=\alpha \mathbf{S}^{\mathcal{N}} \mathbf{Z}+(1-\alpha) \mathbf{S}^{\prime \mathcal{N}} \mathbf{Z}$
其中,加权系数 $\alpha = 0.5$ ,其中的 $\mathbf{S}^{\mathcal{N}}$ 和 $\mathbf{S}^{\prime \mathcal{N}}$ 构造如下 :
$\mathbf{S}_{i j}=\frac{\mathbf{z}_{i} \mathbf{z}_{j}^{\mathbf{T}}}{\left\|\mathbf{z}_{i}\right\|\left\|\mathbf{z}_{j}\right\|}, \quad \forall i, j \in[1, N]$
对于 $\mathbf{S}^{\prime \mathcal{N}}$ 的构造:首先,根据 $\mathbf{S}$ 来选择每个节点的 $1$ 到 $P$ 阶的邻居节点,然后将 $\mathbf{S}$ 中的其他节点 置为 $-1$ ,最后对称化 $\mathbf{S}$ 。

2.3 Hidden Structure Refifining
包括两个方面:
-
- the multi-order observed attributes fusion
- the edge recovery
将 $\widetilde{\mathbf{X}}$ 和 $\dot{\mathcal{A}}= \left\{\dot{\mathbf{A}}^{I}, \dot{\mathbf{A}}^{2}, \ldots, \dot{\mathbf{A}}^{H}\right\}$ 放入 一个共享权重的 Encoder $E$ ,得到其 $h$ 阶的表示:
$\mathbf{Z}^{h(l)}=\sigma\left(\dot{\mathbf{A}}^{h} \mathbf{Z}^{h(l-1)} \mathbf{W}^{(l)}\right)$
注意:上述 $H=3$ ,代表考虑三阶邻居节点。
接着求节点 $n$ 在不同阶的重要性:
${\LARGE a_{n}^{h}=\frac{e^{\left(\mathbf{W}^{h}\left(\mathbf{z}_{n}^{h}\right)^{\mathbf{T}}+\mathbf{b}^{h}\right)}}{\sum\limits _{h=1}^{H} e^{\left(\mathbf{W}^{h}\left(\mathbf{z}_{n}^{h}\right)^{\mathbf{T}}+\mathbf{b}^{h}\right)}}} $
最终的表示如下:
$\mathbf{Z}_{s}=\sum\limits _{h=1}^{H}\left(\mathbf{A t t}^{h}\right)^{\mathbf{T}} \odot \mathbf{Z}^{h}$
其中
-
- $\odot$ 代表着 means matrix product ;
- $\mathbf{A t t}^{h} \in \mathbb{R}^{d \times N}$ 为 $\left[\mathbf{a}_{1}^{h}, \mathbf{a}_{2}^{h}, \ldots, \mathbf{a}_{N}^{h}\right] and \mathbf{a}_{n}^{h} \in \mathbb{R}^{d \times 1}$ ,且 $\mathbf{a}_{n}^{h} \in \mathbb{R}^{d \times 1}$ ;
$\widehat{\mathbf{A}}=\operatorname{Sigmoid}\left(\mathbf{Z}_{s} \mathbf{Z}_{s}^{\mathbf{T}}\right)$
常规的链接预测损失函数如下:
$l_{i j}=-\left[\mathbf{A}_{i j} \ln \widehat{\mathbf{A}}_{i j}+\left(1-\mathbf{A}_{i j}\right) \ln \left(1-\widehat{\mathbf{A}}_{i j}\right)\right]$
由于存在节点特征缺失,本文定义了一个新的超参数控制 边恢复:
$\mathcal{L}_{i j}=\left\{\begin{array}{ll}\gamma l_{i j}, & v_{i}, v_{j} \in \mathcal{V}^{m} \\l_{i j}, & \text { otherwise }\end{array}\right.$
对于所有节点的总损失:
$\mathcal{L}_{s}=\frac{1}{N^{2}} \sum\limits _{i=1}^{N} \sum\limits_{j=1}^{N} \mathcal{L}_{i j}$
2.4 Information Aggregation and Decoding
将上述两个模块的表示进行融合 :
$\mathbf{Z}_{f}=\beta \mathbf{Z}_{a}+(1-\beta) \mathbf{Z}_{s}$
然后走 Encoder :
$\mathbf{Z}^{\prime}(l)=\sigma\left(\tilde{\mathbf{A}} \mathbf{Z}^{\prime}(l-1) \mathbf{W}^{\prime}(l)\right)$
3 Joint Loss and Optimization
联合损失如下:
$\mathcal{L}_{\text {total }}=\lambda \mathcal{L}_{a}+\mathcal{L}_{s}$
4 Conclusion
该论文瞅瞅就行。