论文信息
论文标题:Augmentation-Free Graph Contrastive Learning with Performance Guarantee
论文作者:Haonan Wang, Jieyu Zhang, Qi Zhu, Wei Huang
论文来源:2022, ArXiv
论文地址:download
论文代码:download
1 Introduction
在这项工作中,我们通过 谱理论 的透镜检查增强技术对图数据的影响,重新审视GCL中的这种惯例。
我们发现,图增强保留了低频分量,扰动了图的中高频分量,这有助于GCL算法在同质图上的成功,但由于异质图数据的高频偏好,阻碍了其在异质图上的应用。
2 Preliminary
2.1 Homophilic and Heterophilic Graph
$h_{\text {node }}=\frac{1}{N} \sum_{v_{i} \in \mathcal{V}} \frac{\left|\left\{v_{j}:\left(v_{i}, v_{j}\right) \in \mathcal{E} \wedge y_{i}=y_{j}\right\}\right|}{\left|\left\{v_{j}:\left(v_{i}, v_{j}\right) \in \mathcal{E}\right\}\right|}$
它评估了所有节点的边标签一致性的平均比例。
$h_{\text {edge }}=\frac{\left|\left\{\left(v_{i}, v_{j}\right):\left(v_{i}, v_{j}\right) \in \mathcal{E} \wedge y_{i}=y_{j}\right\}\right|}{E}$
边的同质性是连接同一个类的两个节点的边的比例。
它们都在 $[0,1]$ 的范围内,接近 $1$ 的值对应强同质性,而接近 $0$ 的值表示强异质性。
常用数据集同质性:
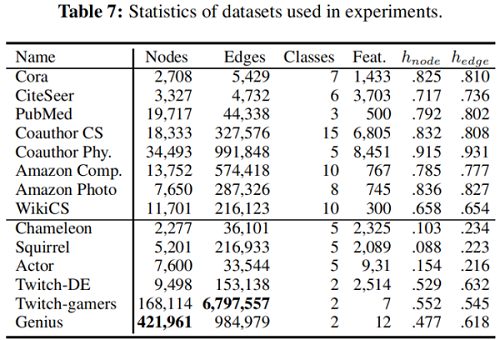
2.2 Graph Laplacian and Variants
我们定义图的拉普拉斯矩阵为 $\mathbf{L}=\mathbf{D}-\mathbf{A}$,其中 $\mathbf{D}=\operatorname{diag}\left(d_{1}, \ldots, d_{N}\right)$,$d_{i}= \sum_{j} \mathbf{A}_{i, j}$。对称标准化拉普拉斯算子,定义为 $\mathbf{L}_{s y m}=\mathbf{D}^{-\frac{1}{2}} \mathbf{L}^{-\frac{1}{2}}=\mathbf{U}^{\top} \mathbf{U}^{\top}$,这里 $\mathbf{U} \in \mathbb{R}^{N \times N}=\left[\mathbf{u}_{1}, \ldots, \mathbf{u}_{N}\right]$,其中,$\mathbf{u}_{i} \in \mathbb{R}^{N}$ 表示 $\mathbf{L}_{s y m}$ 的第 $i$ 个特征向量,而 $\Lambda= \operatorname{diag}\left(\lambda_{1}, \ldots, \lambda_{N}\right)$ 为对应的特征值矩阵。$\lambda_{1}$ 和 $\lambda_{N}$ 分别为最小和最大特征值。
亲和(转移)矩阵可以从拉普拉斯矩阵中推导出,$\mathbf{A}_{\mathrm{sym}}=\mathbf{I}-\mathbf{L}_{\mathrm{sym}}=\mathbf{D}^{-1 / 2} \mathbf{A} \mathbf{D}^{-1 / 2}=\mathbf{U}(\mathbf{I}-\mathbf{\Lambda}) \mathbf{U}^{\top}$。$\mathbf{L}_{\text {sym }}$ 的特征值从 $0$ 到 $2$,广泛应用于谱图神经网络的设计,如图卷积网络(GCN)[18]。
其特征值范围为:$[0,2]$。对于拉普拉斯矩阵,较小的特征值对应于较低的频率[2]。根据之前的工作[6],我们将 $\mathbf{L}_{s y m}$ 在不同频带下的分解分量定义为 $\mathbf{L}_{s y m}^{m} $,其特征值为 $\left[\lambda_{N} \cdot \frac{(m-1)}{M}, \lambda_{N} \cdot \frac{m}{M}\right)$,和 $m \in[1, M]$,$M \in \mathcal{Z}^{+}$ 表示频谱的划分数。更具体地说,$\mathbf{L}_{s y m}^{m}=\mathbf{U} \mathbf{\Lambda}^{m} \mathbf{U}^{\top}$,$\Lambda^{m}= \operatorname{diag}\left(\lambda_{1}^{m}, \ldots, \lambda_{N}^{m}\right)$,其中对于 $i \in[1, N] $。
$\lambda_{i}^{m}=\left\{\begin{array}{l}\lambda_{i}, \text { if } \lambda_{i} \in\left[\lambda_{N} \cdot \frac{(m-1)}{M}, \lambda_{N} \cdot \frac{m}{M}\right) \\0, \text { otherwise }\end{array}\right.$
注意,所有分解分量的和等于对称归一化拉普拉斯矩阵 $\mathbf{L}_{s y m}=\sum\limits _{m=0}^{\lceil N / M\rceil} \mathbf{L}_{s y m}^{m}$ 。
3 Revisiting Graph Augmentations
常用数据增强的方法:
-
- attribute masking
- edge adding
- edge dropping
- graph diffusion
3.1 Effect of Augmentations on Geometric Structure
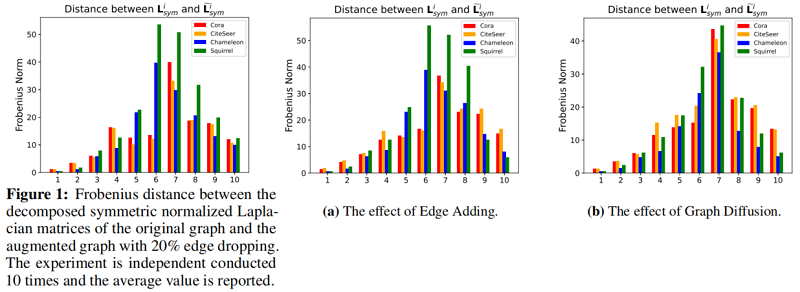
由 2.2 节知道第 $m$ 个分量对称归一化拉普拉斯算式定义为 $\mathbf{L}_{s y m}^{m}$。相应地,将增广图的第 $m$ 个分量对称归一化拉普拉斯算子表示为 $\widetilde{\mathbf{L}}_{s y m}^{m}$。为测量不同频率分量的图增强影响,使用 F范数 作为度量来测量距离,$\left\|\mathbf{L}_{s y m}^{m}-\widetilde{\mathbf{L}}_{s y m}^{m}\right\|_{F}$。
以下为分别为 Edge dropping、Edge Adding、Graph Diffusion 的实验结果:
3.2 Effect of Augmentations on Features
为了进一步研究常用的图增强方法属性掩蔽对谱图节点属性的影响。我们将傅里叶变换和傅里叶反变换表示为 $\mathcal{F}(\cdot)$ 和 $\mathcal{F}^{-1}(\cdot)$。我们用 $\mathbf{H}^{\mathcal{F}}$ 来表示变换后的节点特征。因此,我们有 $\mathbf{H}^{\mathcal{F}}= \mathcal{F}(\mathbf{X})$ 和 $\mathbf{X}=\mathcal{F}^{-1}\left(\mathbf{H}^{\mathcal{F}}\right)$ 。我们分解了节点属性 $\mathbf{X}=\left\{\mathbf{X}^{l}, \mathbf{X}^{h}\right\}$,其中 $\mathbf{X}^{l}$ 和 $\mathbf{X}^{h}$ 分别表示 $X$ 的低频分量和高频分量。我们有以下四个方程式:
$\begin{array}{left}\mathbf{H}^{\mathcal{F}}=\mathcal{F}(\mathbf{X})\\\mathbf{H}^{l}, \mathbf{H}^{h}=t\left(\mathbf{H}^{\mathcal{F}} ; R\right)\\\mathbf{X}^{l}=\mathcal{F}^{-1}\left(\mathbf{H}^{l}\right)\\ \mathbf{X}^{h}=\mathcal{F}^{-1}\left(\mathbf{H}^{\mathcal{F}}\right)\end{array}$
其中 $t(\cdot ; R)$ 表示一个阈值函数,根据超参数 $m$ 分离低频和高频分量。因为 $\mathbf{H}^{f}$ 左侧的列对应于低频分量,所以我们将 $t(\cdot ; m)$ 定义为:
$\mathbf{H}_{i j}^{l}=\left\{\begin{array}{ll}\mathbf{H}_{i j}^{\mathcal{F}}, & \text { if } j \leq R \\0, & \text { otherwise }\end{array}, \quad \mathbf{H}_{i j}^{h}=\left\{\begin{array}{ll}0, & \text { if } j \leq R \\\mathbf{H}_{i j}^{\mathcal{F}}, & \text { otherwise }\end{array}\right.\right.$
进一步,我们将属性掩蔽的节点属性表示为 $\widetilde{\mathbf{X}}$,其对应的低高频分量表示为 $\widetilde{\mathbf{X}}^{l}$、$\widetilde{\mathbf{X}}^{h}$。通过计算矩阵的 F范数 距离 ,研究了属性掩蔽对节点特征的影响,并将 $\left\|\mathbf{X}^{l}-\tilde{\mathbf{X}}^{l}\right\|_{F}$ 表示为 F-norm-low,$\left\|\mathbf{X}^{h}-\widetilde{\mathbf{X}}^{h}\right\|_{F}$ 表示为 $\left\|\mathbf{X}^{h}-\widetilde{\mathbf{X}}^{h}\right\|_{F}$。四个数据集的结果汇总如表2所示。我们令人惊讶地发现,属性掩蔽总是会影响高频分量。
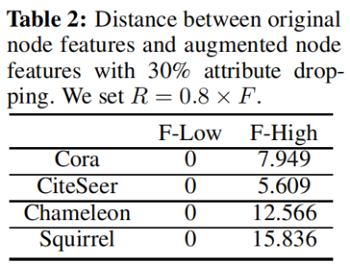
正如之前的工作[3,21]所示,对于异质图,高频分量所携带的信息对下游的分类性能更为有效。然而,正如我们所分析的,中高频信息被常用的图增强技术干扰。对于信息最大化目标,学习到的嵌入[54]只鼓励捕获不变信息(低频)。虽然现有的图增强算法促进了GCL在传统(同同性)基准上的成功,但当高频信息是至关重要的(异质图)时,它们导致次优表示。
4 Method
为了设计一个通用的自监督信号,我们有动力分析聚合节点特征 $Z$(第4.1节)的浓度特性。即在不同的同质性程度下,同一类节点之间更接近。利用集中特性,我们提出了一种无增强的方法(第4.2节),AF-GCL,来构建用于对比学习的正对和负对。
4.1 Analysis of Aggregated Features
$\mathbf{x}_{i}=y_{i} \boldsymbol{\mu}+\frac{\mathbf{q}_{i}}{\sqrt{F}}$
其中,随机变量qi∈RF具有独立的标准正常条目,而 $y_{i} \in\{-1,1\}$ 表示滥用符号的潜在类。然后,具有 $y_{i}$ 类的节点的特征根据 $y_{i}$ 遵循相同的分布,即 $\mathbf{x}_{i} \sim P_{y_{i}}(\mathbf{x}) $。此外,我们对邻域模式进行了假设,对于节点 $i$,其邻域的标签是从一个分布 $P\left(y_{i}\right)$ 中独立采样的。
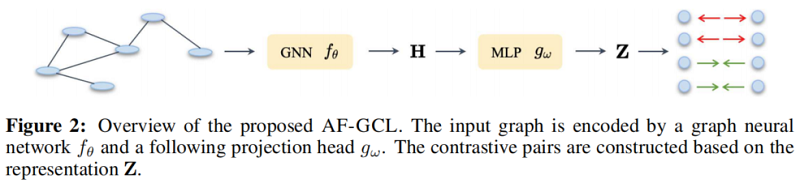
Remark.上述假设表明,邻居的标签是由一个仅依赖于中心节点的标签的分布产生的,中心节点包含同质性和异质性的情况。基于此假设,我们证明了以下引理1,即所有具有相同标签的聚合节点特征都具有相同的嵌入性。具体来说,我们通过 $Z$ 通过GCN和MLP定义学习嵌入,如图2所示,$Z_i$ 是相对于输入 $x_i$ 的学习嵌入。为了简化分析,我们在GCN和MLP中引入 $W$ 作为非线性下降后的等效线性权重。
Lemma 1 (Adaption of Theorem 1 in [26]) Consider a graph $G$ following the graph assumption and $Eq. 4$, then the expectation of embedding is given by
$\mathbb{E}\left[\mathbf{Z}_{i}\right]=\mathbf{W} \mathbb{E}_{y \sim P\left(y_{i}\right), \mathbf{x} \sim P_{y}(\mathbf{x})}[\mathbf{x}]\quad\quad\quad(5)$
Furthermore, with probability at least 1-\delta over the distribution for graph, we have:
$\left\|\mathbf{Z}_{i}-\mathbb{E}\left[\mathbf{Z}_{i}\right]\right\|_{2} \leq \sqrt{\frac{\sigma_{\max }^{2}(\mathbf{W}) F \log (2 F / \delta)}{2 \mathbf{D}_{i i}\|\mathbf{x}\|_{\psi_{2}}}}\quad\quad\quad(6)$
where the sub-gaussian norms $\|\mathbf{x}\|_{\psi_{2}} \equiv \min _{i}\left\|\mathbf{x}_{i, d}\right\|_{\psi_{2}}$, $d \in[1, F]$ and $\sigma_{\max }^{2}(\mathbf{W})$ is the largest singular value of $\mathbf{W}$ , because each dimension in feature is independently distributed.
我们在附录D.1中留下了上述引理的证明。上面的引理表明,对于每个节点的特征和邻域模式根据节点标签从分布中采样的任何图,GCN模型能够将具有相同标签的节点映射到嵌入空间中以期望为中心的区域。
4.2 Augmentation-Free Graph Contrastive Learning (AF-GCL)
以上理论分析表明,对于每个类,从邻域聚合中得到的嵌入将集中于属于该类的嵌入期望。受此启发,我们设计了基于所获得的嵌入算法的自监督信号,并提出了一种新的无增强图对比学习算法AF-GCL,该算法选择相似的节点作为正节点对。如前面的分析所示,浓度性质与同质性和异亲性假设无关,因此AF-GCL在亲同性和异亲同性图上都能很好地推广。无增强设计使AF-GCL摆脱了普遍采用的双分支设计[57],显著降低了计算开销。
如图2所示,在每次迭代中,所提出的框架首先用一个由 $\mathbf{H}=f_{\theta}(\mathbf{X}, \mathbf{A})$ 表示的图编码器 $f_{\theta}$ 对图进行编码。值得注意的是,我们的框架允许在没有任何约束的情况下进行网络架构的各种选择。然后,利用 L2-normalization 的MLP投影头 $g_{\omega}$ 将节点嵌入投影到隐藏表示 $\mathbf{Z}=g_{\omega}(\mathbf{H})$ 中。
在每次迭代中,采样 $b$ 个节点形成种子节点集 $S$;它们周围的 $t$ 跳邻居包括节点池 $P$。对于每个种子节点 $v_{i} \in S$,选择节点池中相似性 $top-K_{\text {pos }}$ 节点作为正集,表示为 $S_{\text {pos }}^{i}=\left\{v_{i}, v_{i}^{1}, v_{i}^{2}, \ldots, v_{i}^{K_{\text {pos }}}\right\} $。具体来说,
由于隐表示是归一化的,所以隐表示的内积等于余弦相似度。该框架的优化目标如下:
$\mathcal{L}_{g c l}=-2\mathbb{E}_{\underset{v_{i}+\sim U n i\left(S_{p o s}^{i}\right)}{v_{i} \sim U n i(\mathcal{V})} } \left[\mathbf{Z}_{i}^{\top} \mathbf{Z}_{i+}\right]+\mathbb{E}_{\underset{v_{k}+\sim U n i\left(\mathcal{V}\right)}{v_{j} \sim U n i(\mathcal{V})} }\left[\left(\mathbf{Z}_{j}^{\top} \mathbf{Z}_{k}\right)^{2}\right] \quad\quad\quad(8)$
其中,节点 $v_{i^{+}}$、$v_{j}$ 和 $v_{k}$ 从它们对应的集合中均匀采样。总的来说,算法1总结了训练算法AF-GCL在算法1中。

5 Experiments
编码器
两层的GCN:
$\mathrm{GCN}_{i}(\mathbf{X}, \mathbf{A})=\sigma\left(\overline{\mathbf{D}}^{-\frac{1}{2}} \overline{\mathbf{A}} \overline{\mathbf{D}}^{-\frac{1}{2}} \mathbf{X} \mathbf{W}_{i}\right)$
对比损失 $\text{Eq.8}$:
$\widehat{\mathcal{L}}=-\frac{2}{N \cdot K_{\text {pos }}} \sum\limits_{i}^{N} \sum\limits_{i^{+}}^{K_{\text {pos }}}\left[\mathbf{Z}_{i}^{\top} \mathbf{Z}_{i+}\right]+\frac{1}{N \cdot K_{n e g}} \sum\limits_{j}^{N} \sum\limits_{k}^{K_{n e g}}\left[\left(\mathbf{Z}_{j}^{\top} \mathbf{Z}_{k}\right)^{2}\right]\quad\quad\quad(12)$
其中,为了近似负对的期望($\text{Eq.8}$ 的第二项),我们为每个节点采样 $K_{n e g}$ 节点。
实验结果
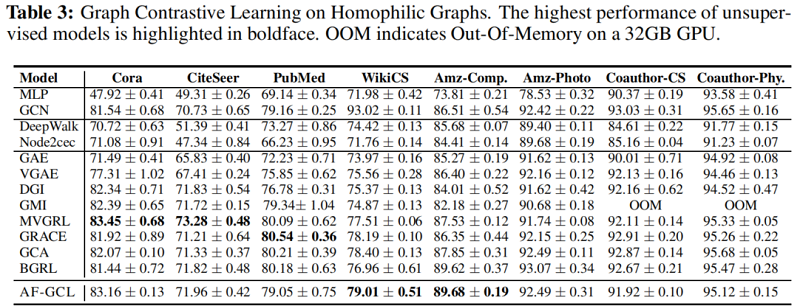
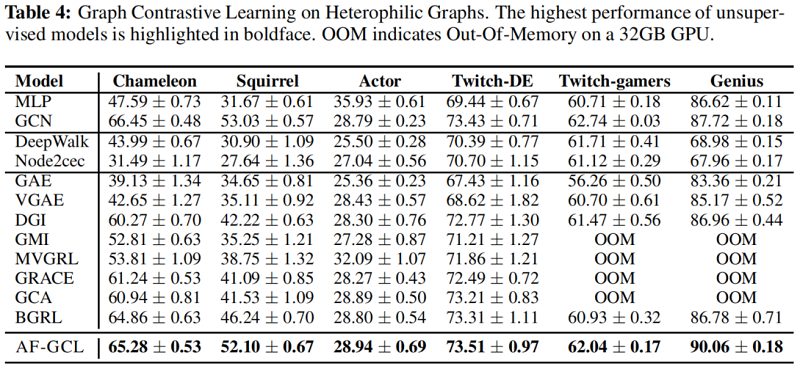
6 Conclusion
在这项工作中,我们首先研究图增强技术的影响——现有的图对比学习算法的一个关键部分。具体来说,它们倾向于保留低频信息和扰动高频信息,这主要有助于基于增强的GCL算法在同质图上的成功,但限制了其在异图上的应用。然后,在对图神经网络聚合特征进行理论分析的激励下,我们提出了一种无增强图对比学习方法AF-GCL,其中基于聚合特征构建自监督信号。我们进一步为AF-GCL的性能和疗效分析提供了理论保证。根据经验,我们表明AF-GCL可以在8个同同图基准和6个异同图基准上优于SOTA方法,计算开销明显更少。诚然,我们主要关注的是节点分类问题。我们想在未来留下对回归问题和图分类问题的探索。
修改历史
2022-06-15 创建文章