论文解读（DCRN）《Deep Graph Clustering via Dual Correlation Reduction》 Learner

论文信息

论文标题：Deep Graph Clustering via Dual Correlation Reduction
论文作者：Yue Liu, Wenxuan Tu, Sihang Zhou, Xinwang Liu, Linxuan Song, Xihong Yang, En Zhu
论文来源：2022, AAAI
论文地址：download 
论文代码：download

1 介绍

　　表示崩塌问题：倾向于将所有数据映射到相同表示。

　　   

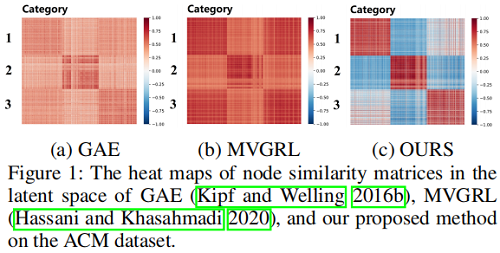
　　创新点：提出使用表示相关性来解决表示坍塌的问题。

2 方法

2.1 整体框架

　　   

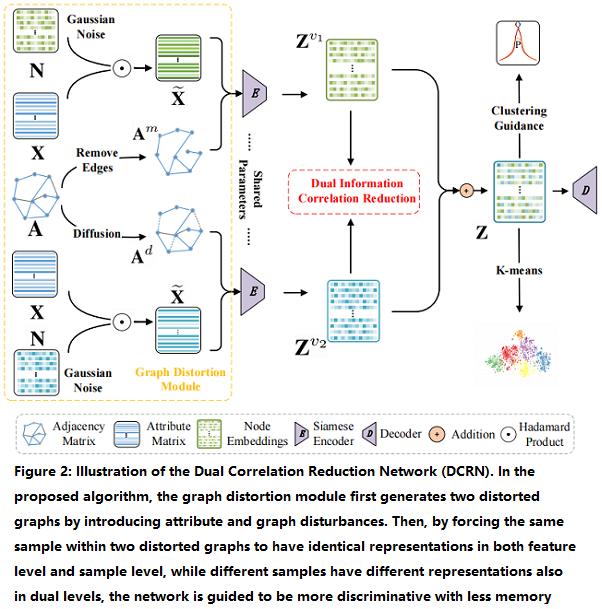
　　该框架包括两个模块：

• • a graph distortion module；
  • a dual information correlation reduction (DICR) module；

2.2 相关定义

　　

　　$\widetilde{\mathbf{A}}=\mathbf{D}^{-1}(\mathbf{A}+\mathbf{I})\quad\quad \text{and} \quad\quad  \widetilde{\mathbf{A}} \in \mathbb{R}^{N \times N} $

2.3  Graph Distortion Module

Feature Corruption：

　　首先从高斯分布矩阵 $ \mathcal{N}(1,0.1)$ 采样一个随机噪声矩阵 $\mathbf{N} \in \mathbb{R}^{N \times D}  $，然后得到破坏后的属性矩阵  $\widetilde{\mathbf{X}} \in \mathbb{R}^{N \times D}$ ：

　　　　$\widetilde{\mathbf{X}}=\mathbf{X} \odot \mathbf{N} \quad\quad\quad(1)$

Edge Perturbation：

• similarity-based edge removing

　　根据表示的余弦相似性先计算一个相似性矩阵，然后根据相似性矩阵种的值小于 $0.1$ 将其置 $0$ 来构造掩码矩阵（masked matrix）$\mathbf{M} \in \mathbb{R}^{N \times N}$。对采用掩码矩阵处理的邻接矩阵做标准化：

　　　　$\mathbf{A}^{m}=\mathbf{D}^{-\frac{1}{2}}((\mathbf{A} \odot \mathbf{M})+\mathbf{I}) \mathbf{D}^{-\frac{1}{2}}\quad\quad\quad(2)$

• graph diffusion

　　　　$\mathbf{A}^{d}=\alpha\left(\mathbf{I}-(1-\alpha)\left(\mathbf{D}^{-\frac{1}{2}}(\mathbf{A}+\mathbf{I}) \mathbf{D}^{-\frac{1}{2}}\right)\right)^{-1}\quad\quad\quad(3)$

2.4  Dual Information Correlation Reduction

　　框架如下：

　　  

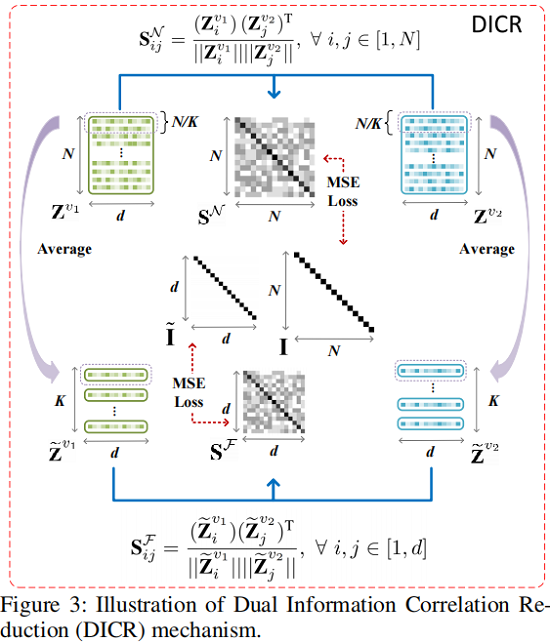
Sample-level Correlation Reduction

　　对于由 siamese graph encoder 学习到的双视图节点嵌入 $ \mathbf{Z}^{v_{1}} $ 和  $\mathbf{Z}^{v_{2}} $，我们首先通过以下方法计算交叉视图样本相关性矩阵$\mathbf{S}^{\mathcal{N}} \in \mathbb{R}^{N \times N}$ ：

　　　　${\large \mathbf{S}_{i j}^{\mathcal{N}}=\frac{\left(\mathbf{Z}_{i}^{v_{1}}\right)\left(\mathbf{Z}_{j}^{v_{2}}\right)^{\mathrm{T}}}{\left\|\mathbf{Z}_{i}^{v_{1}}\right\|\left\|\mathbf{Z}_{j}^{v_{2}}\right\|}} , \forall i, j \in[1, N]\quad\quad\quad(4)$

　　其中：$\mathbf{S}_{i j}^{\mathcal{N}} \in[-1,1] $ 表示第一个视图中第 $i$ 个节点嵌入与第二个视图中第 $j$ 个节点嵌入的余弦相似度。

　　然后利用 $\mathbf{S}^{\mathcal{N}}$ 计算：

　　　　$\begin{aligned}\mathcal{L}_{N} &=\frac{1}{N^{2}} \sum\limits^{N}\left(\mathbf{S}^{\mathcal{N}}-\mathbf{I}\right)^{2} \\&=\frac{1}{N} \sum\limits_{i=1}^{N}\left(\mathbf{S}_{i i}^{\mathcal{N}}-1\right)^{2}+\frac{1}{N^{2}-N} \sum\limits_{i=1}^{N} \sum\limits_{j \neq i}\left(\mathbf{S}_{i j}^{\mathcal{N}}\right)^{2}\end{aligned}\quad\quad\quad(5)$

　　$\mathcal{L}_{N}$ 的第一项鼓励 $\mathbf{S}^{\mathcal{N}}$ 中的对角线元素等于 $1$，这表明希望两个视图的节点表示一致性高。第二项使 $\mathbf{S}^{\mathcal{N}}$ 中的非对角线元素等于 $0$，以最小化在两个视图中不同节点的嵌入之间的一致性。

Feature-level Correlation Reduction

　　首先，我们使用读出函数 $\mathcal{R}(\cdot): \mathbb{R}^{d \times N} \rightarrow \mathbb{R}^{d \times K}$ 将双视图节点嵌入 $\mathbf{Z}^{v_{1}}$ 和 $\mathbf{Z}^{v_{2}} $ 分别投影到 $\widetilde{\mathbf{Z}}^{v_{1}} $ 和 $\widetilde{\mathbf{Z}}^{v_{2}} \in \mathbb{R}^{d \times K}$ 中，该过程公式化为：

　　　　$\widetilde{\mathbf{Z}}^{v_{k}}=\mathcal{R}\left(\left(\mathbf{Z}^{v_{k}}\right)^{\mathrm{T}}\right)\quad\quad\quad(6)$

　　同样此时计算 $\widetilde{\mathbf{Z}}^{v_{1}} $ 和 $\widetilde{\mathbf{Z}}^{v_{2}}$ 之间的相似性：

　　　　${\large \mathbf{S}_{i j}^{\mathcal{F}}=\frac{\left(\widetilde{\mathbf{Z}}_{i}^{v_{1}}\right)\left(\widetilde{\mathbf{Z}}_{j}^{v_{2}}\right)^{\mathrm{T}}}{\left\|\widetilde{\mathbf{Z}}_{i}^{v_{1}}\right\|\left\|\widetilde{\mathbf{Z}}_{j}^{v_{2}}\right\|}} , \forall i, j \in[1, d]\quad\quad\quad(7)$

　　然后利用 $\mathbf{S}^{\mathcal{F}}$ 计算：

　　　　$\begin{aligned}\mathcal{L}_{F} &=\frac{1}{d^{2}} \sum\limits^{\mathcal{S}}\left(\mathbf{S}^{\mathcal{F}}-\widetilde{\mathbf{I}}\right)^{2} \\&=\frac{1}{d^{2}} \sum\limits_{i=1}^{d}\left(\mathbf{S}_{i i}^{\mathcal{F}}-1\right)^{2}+\frac{1}{d^{2}-d} \sum\limits_{i=1}^{d} \sum\limits_{j \neq i}\left(\mathbf{S}_{i j}^{\mathcal{F}}\right)^{2}\end{aligned}\quad\quad\quad(8)$

　　下一步将两个视图的表示合并得：

　　　　$\mathbf{Z}=\frac{1}{2}\left(\mathbf{Z}^{v_{1}}+\mathbf{Z}^{v_{2}}\right)\quad\quad\quad(9)$

　　上述所提出的 DICR 机制从样本视角和特征水平的角度都考虑了相关性的降低。这样，可以过滤冗余特征，在潜在空间中保留更明显的特征，从而学习有意义的表示，避免崩溃，提高聚类性能。

Propagated Regularization

　　为了缓解网络训练过程中出现的过平滑现象，我们引入了一种传播正则化方法，即：

　　　　$\mathcal{L}_{R}=J S D(\mathbf{Z}, \tilde{\mathbf{A}} \mathbf{Z})\quad\quad\quad(10)$

　　综上 DICR ，模块的目标函数为：

　　　　$\mathcal{L}_{D I C R}=\mathcal{L}_{N}+\mathcal{L}_{F}+\gamma \mathcal{L}_{R}\quad\quad\quad(11)$

2.5 目标函数

　　总损失函数如下：

　　　　$\mathcal{L}=\mathcal{L}_{D I C R}+\mathcal{L}_{R E C}+\lambda \mathcal{L}_{K L}\quad\quad\quad(12)$

　　分别代表着 DICR的损失$\mathcal{L}_{D I C R}$、重建损失$\mathcal{L}_{R E C}$ 和聚类损失 $ \mathcal{L}_{K L}$。

　　后面两个损失参考 DFCN。

　　【我本文认为它这个相关性的方法存在不合理之处，没考虑邻居节点，本文之所以有效，也许可能正是它后面加了一个自表达模型】

3 实验

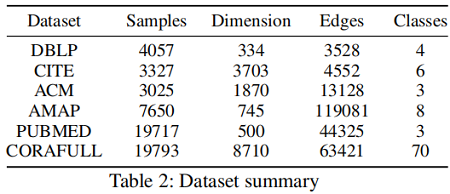
　　数据集：

　　

　　基线实验：

　　

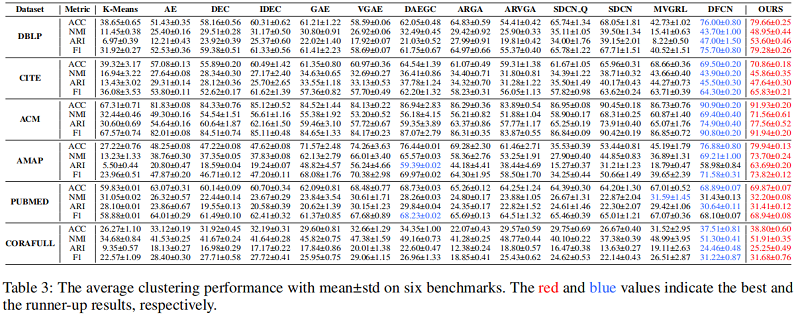
4 结论

　　在这项工作中，我们提出了一种新的自监督深度图聚类网络，称为双相关减少网络(DCRN)。在我们的模型中，引入了一种精心设计的双信息相关减少机制来降低样本和特征水平上的信息相关性。利用这种机制，可以过滤掉两个视图中潜在变量的冗余信息，可以很好地保留两个视图的更鉴别特征。它在避免表示崩溃以实现更好的聚类方面起着重要的作用。在6个基准测试上的实验结果证明了DCRN的优越性。