论文解读（GAN）《Generative Adversarial Networks》

论文信息

论文标题：Generative Adversarial Networks
论文作者：Ian J. Goodfellow, Jean Pouget-Abadie ......
论文来源：2014, NIPS
论文地址：download 
论文代码：download 

1 Introduction

　　本文提出 GAN 框架， 通过一个对抗来估计生成模型。该框架同时训练两个模型：

• • 生成模型（Generative model）$G$ 用于捕获数据分布；
  • 判别模型（Discriminative model）$D$ 用于识别真实数据；

　　 $G$ 主要做的是：使得虚假样本尽可能的欺骗判别模型 $D$  ，使其辨别不出来。

　　 $D$ 主要做的是：将生成模型 $G$ 生成的虚假样本与真实样本识别出来。

　　该过程可以总结为：This framework corresponds to a minimax two-player game（minmax 双人博弈）.

　　监督学习方法可以分为生成方法 (generative approach) 和判别方法 (discriminative approach) 。所学到的模型分别称为 生成模型 (generative model) 和判别模型 (discriminative model)。生成方法由数据学习联合概率分布 $P(X, Y)$ ，然后求出条 件概率分布 $P(Y \mid X)$ 作为预测的模型，即生成模型:

　　　　$P(Y \mid X)=\frac{P(X, Y)}{P(X)}$

　　在机器学习领域判别模型是一种对未知数据 $y$ 与已知数据 $x$ 之间关系进行建模的方法。判别模型是一种基于概率理论的方法。已知输入变量 $x$ ，判别模型通过构建条件概率分布 $P(y|x)$ 预测 $y $。

　　整体框架：

　　

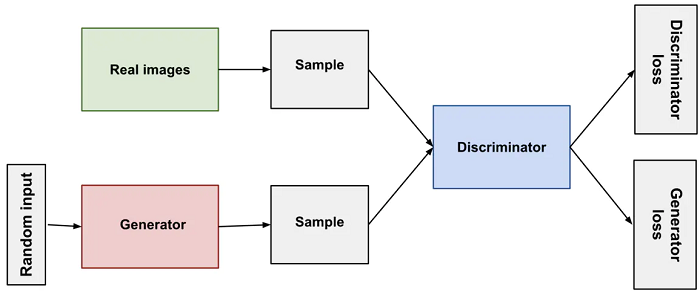
　　Generator 和 Discriminator 都是神经网络，Generator 的数据将连接到 Discriminator 的输入，而 Discriminator 的分类结果将通过 loss 并反向传播给 Generator 进行权重更新。如果 Generator 训练的很好，Discriminator 将会难以识别真假，精度开始下降。

　　GAN中的 Discriminator 是一个分类器，在 Discriminator 的训练期间，Generator 没有在训练而仅仅是在产生负样本。Discriminator 连接两个 loss 函数，在 Discriminator 的训练期间，Discriminator 忽略掉 Generator loss，仅仅使用 Discriminator loss。在 Generator 的训练期间才会用到 Generator loss。

2 Method

　　本文选取生成器和判别器都是 MLP 。

　　定义：

• • 数据 $x$；
  • 数据 $x$ 在生成器上的数据分布 $p_g​ $；
  • 先验的输入噪声变量分布 $p_{z}(z) $；
  • 噪声变量的映射  $G\left(z ; \theta_{g}\right) $ ；
  • 判别器 $D\left(x ; \theta_{d}\right)$  输出 $x$ 来自真实数据分布而不是  $p_{g}$  的概率；

　　目标函数如下（二分类交叉熵）:

　　　　$\underset {G}{\text{min }}\underset {D}{\text{max }}V(D, G)=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))]\quad \quad \quad (1)$

　　其中，

• • $x$  是真实数据；
  • $D(X)$  表示将 $x$ 预测为真实数据的概率（分数）；
  • $G(z)$  表示生成器生成的数据；
  • $D(G(z))$  表示将生成数据预测为真实数据的概率（分数）；

　　例子：

　　

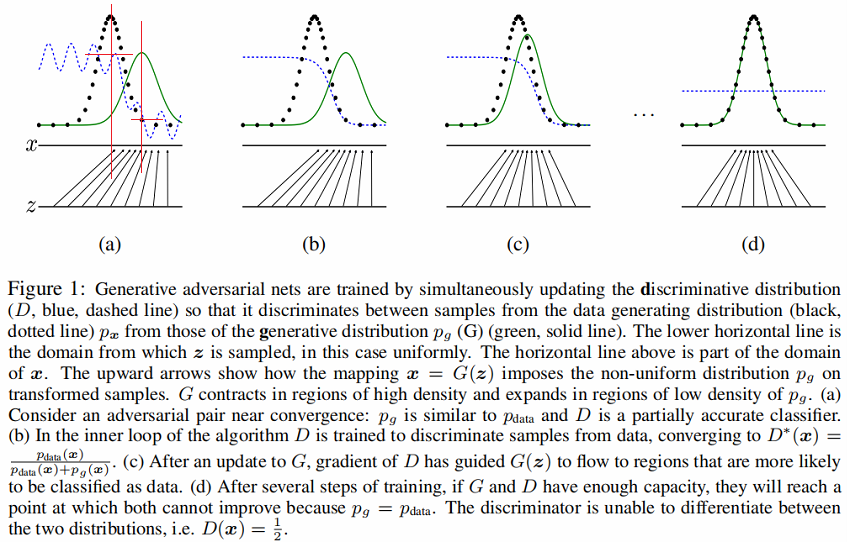
• 判别分布D（蓝色、虚线）

• 数据生成分布 $p_x$（黑色，虚线）

• 噪声生成分布 $P_{g}(G)$（G 绿色，实线）

• 下面的水平线为均匀采样 $z$ 的区域，上面的水平线为 $x$ 的部分区域。

• 朝上的箭头显示映射 $x=G(z)$ 如何将非均匀分布 $p_{g}$ 作用在转换后的样本上。

• $G$ 在 $p_{g}$ 高密度区域收缩，且在 $p_{g}$ 的低密度区域扩散。

• Figure1 (a) 考虑一个接近收敛的对抗的模型对: $p_{g}$  与 $p_{\text {data }}$  分布相似，且 $D$  是个部分准确的分类器【密度中心部分可以大致识别出来】。（可以发现$p_{g}$  与 $p_{\text {data }}$ 的密度中心不一样，判别器 $D$ 在 $p_{data}$ 的密度中心值高，在 $p_{g}$的密度中心值低。（红色区域相交部分））

• Figure1 (b) 在算法的内循环中，训练 $D$  来判别数据中的样本，收敛到：$ D^{*}(X)=\frac{p_{\text {data }}(x)}{p_{\text {data }}(x)+p_{g}(x)} $。

• Figure1 (c) 在 G 更新后， $D$  的梯度引导  $G(z) $ 与真实数据分布越发接近。

• Figure1 (d) 经过若干步训练后，如果 $G$  和 $D$  性能足够，它们接近某个稳定点并都无法继续提高性能，因为此时 $p_{g}=p_{\text {data }}$  。判别器将无法区分训练数据分布和生成数据分布，即 $D(x)=\frac{1}{2}$  。

3 Theoretical Results

算法：

　　

3.1 Global Optimality of $p_g = p_{data}$

3.1.1 最优判别器

　　Proposition 1. For $G$ fixed, the optimal discriminator $D$ is

　　　　${\large D_{G}^{*}(\boldsymbol{x})=\frac{p_{\text {data }}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}} \quad \quad \quad (2)$

　　证明：

　　　　首先考虑将生成器  $G$  固定， 优化最优判别器 $D$。此时最大化 $V (G, D)=V (D)$ ：

　　　　$\begin{aligned}V(G, D) =V (D)&=\int_{\boldsymbol{x}} p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x})) d x+\int_{\boldsymbol{z}} p_{\boldsymbol{z}}(\boldsymbol{z}) \log (1-D(g(\boldsymbol{z}))) d z \\&=\int_{\boldsymbol{x}} p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x}))+p_{g}(\boldsymbol{x}) \log (1-D(\boldsymbol{x})) d x\end{aligned}\quad \quad \quad (3)$

　　回忆：$x=G(z)$  ，这里 $g(z)$ 可以看成是 $G(z)$  函数空间中的一个个例。$p_g(x)$  代替 $p_z(z)$，从 $z$ 域转换到 $x$ 域。

　　令 $p_{data}(x)$ 为 $a$，$p_{g}(x)$ 为 $b$，$D(x)$ 为 $y$。 对于任意的  $(a, b) \in \mathbb{R}^{2} \backslash\{0,0\} $，函数 $y \rightarrow a \log (y)+b \log (1-y) $ 在 $ \frac{a}{a+b}\in  [0,1]  $ 取最值。

　　请注意，$D$ 可以被解释为条件概率  $P(Y=y \mid \boldsymbol{x})$  的最大对数似然估计。这里，$Y$ 代表着  $\boldsymbol{x}$  来自  $p_{\text {data }}$  (with  $y=1$  ) 或者来自  $p_{g}$  (with  $y=0 $ )。

　　Eq. 1 可以转换为：

　　　　$\begin{aligned}C(G) &=\max _{D} V(G, D) \\&=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{z} \sim p_{z}}\left[\log \left(1-D_{G}^{*}(G(\boldsymbol{z}))\right)\right] \\&=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \left(1-D_{G}^{*}(\boldsymbol{x})\right)\right] \\&=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log \frac{p_{\text {data }}(\boldsymbol{x})}{P_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \frac{p_{g}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right]\end{aligned}\quad \quad \quad (4)$

3.1.2 最优生成器

　　Theorem 1. The global minimum of the virtual training criterion  $C(G)$  is achieved if and only if  $p_{g}=p_{\text {data. }}$ . At that point,  $C(G)$  achieves the value  $-\log 4$ .

　　证明：

　　　　当 $p_{g}=p_{\text {data }}$ 时，最优判别器

　　　　${\large D_{G}^{*}(\boldsymbol{x}) =\frac{p_{\text {data }}(x)}{p_{\text {data }}(x)+p_{g}(x)}=\frac{1}{2}} $

　　　　此时目标函数 $V (G, D)=V (G)$ 

　　　　$ \begin{array}{l} V(G,D)&=V(G)\\&=\int_{x} p_{\text {data }}(x) \log \frac{p_{\text {data }}(x)}{p_{\text {data }}(x)+p_{g}(x)}+p_{g}(x) \log \left(1-\frac{p_{\text {data }}(x)}{p_{\text {data }}(x)+p_{g}(x)}\right) d x\end{array} $

　　　　利用最优判别器 ${\large D_{G}^{*}(\boldsymbol{x}) =\frac{p_{\text {data }}(x)}{p_{\text {data }}(x)+p_{g}(x)}=\frac{1}{2}} $，对 $V (G)$ 做变换得：

　　　　$\begin{array}{l} V(G,D)&=V(G)\\&=-\log 2 \int_{x} p_{g}(x)+p_{\text {data }}(x) d x\\&\quad+\int_{x} p_{\text {data }}(x)\left(\log 2+\log \frac{p_{\text {data }}(x)}{p_{\text {data }}(x)+p_{g}(x)}\right)+p_{g}(x)\left(\log 2+\log \frac{p_{g}(x)}{p_{\text {data }}(x)+p_{g}(x)}\right) d x \end{array}$

　　　　其中：

　　　　$\begin{array}{l} -\log 2 \int_{x} p_{g}(x)+p_{data }(x) d x\\=-2 \log 2\int_{x} p_{data}(x)dx\\=-\log4\end{array}$

　　　　$\begin{array}{l}\log 2+\log \frac{p_{\text {data }}(x)}{p_{\text {data }}(x)+p_{g}(x)}&=\log \frac{2 p_{\text {data }}(x)}{p_{\text {data }}(x)+p_{g}(x)}\\&=\log \frac{p_{\text {data }}(x)}{\left(p_{\text {data }}(x)+p_{g}(x)\right) / 2}\end{array} $

　　　　$\begin{array}{l}\log 2+\log \frac{p_{g }(x)}{p_{\text {data }}(x)+p_{g}(x)}&=\log \frac{2 p_{g }(x)}{p_{\text {data }}(x)+p_{g}(x)}\\&=\log \frac{p_{g }(x)}{\left(p_{\text {data }}(x)+p_{g}(x)\right) / 2}\end{array} $

　　　　所以，最终结果为：

　　　　$\begin{array}{l} V(G,D)&=V(G)\\&=-\log 4+D_{K L}\left(p_{\text {data }} \| \frac{p_{\text {data }}+p_{g}}{2}\right)+\left(p_{g} \| \frac{p_{\text {data }}+p_{g}}{2}\right)\end{array}\quad \quad \quad (5)$

　　　　由于KL散度的非负性，得 $C(G)$ 的最小值为 $−\log4  $。

Tips
　　相对熵 (Relative Entropy) 也称 KL 散度。

　　在机器学习中，$P$ 往往用来表示样本的真实分布，$Q$ 用来表示模型所预测的分布，那么KL散度就可以计算两个分布的差异，也就是Loss损失值。

　　　　$D_{K L}(P \| Q)=E_{p(x)}\left[\log \frac{p(x)}{q(x)}\right]=\int_{x} p(x) \log \frac{p(x)}{q(x)}$

• KL散度具有非负性。
• 当且仅当 $P$ ， $Q$ 在离散型变量下是相同的分布时，即 $ p(x)=q(x)$ ， $ D_{K L}(P \| Q)=0$ 。
• K L 散度衡量了两个分布差异的程度，经常被视为两种分布间的距离。
• 请注意， $D_{K L}(P \| Q) \neq D_{K L}(Q \| P)$  ，即 $K L$  散度没有对称性。

 　　从KL的散度定义式可以看出其值域范围为 $[-\infty ,\infty]$ ，且不具有对称性，所以这里将 Eq.5. 转变为JS散度。

　　　　$C(G)=-\log (4)+2 \cdot J S D\left(p_{data} \| p_{g}\right)\quad \quad \quad (6)$

 　　为什么选择JS散度：

• • JS散度具有非负性质
  • JS散度的值域范围在 $[0,1]$ ，$p$ 和 $q$ 分布相同的时候为 $0$，完全不同的时候为 $1$。

3.2 Convergence of Algorithm 1

　　Proposition 2. If $G$ and $D$ have enough capacity, and at each step of Algorithm 1, the discriminator is allowed to reach its optimum given $G $, and $p_{g}$ is updated so as to improve the criterion

　　　　$\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \left(1-D_{G}^{*}(\boldsymbol{x})\right)\right]$

　　then $p_{g}$ converges to $p_{data }$

4 Experiments

　　数据集：Minist、TFD 以及 CIFAR-10。

　　生成器 Generator 使用的激活函数有 ReLU 和 sigmoid，判别器 Discirminator 使用的激活函数是 maxout。

　　Dropout  算法被用于判别器网络的训练。

　　虽然理论上可以在生成器的中间层使用 Dropout 和 其他噪声，但这里仅在 generator network 的最底层使用噪声输入。

　　对 $G$ 生成的样本拟合  Gaussian Parzen window，并报告该分布下的  log-likelihood，来估计  $p_{g}$  下测试集数据的概率。高斯分布中的参数  $\sigma$  通过验证集的交叉验证得到的。

　　 Breuleux et al.引入该过程用于不同的似然难解生成模型上，结果在 Table1 中：

　　　　

　　我们可以看到结果中方差很大，并且在高维模型中表现不好。

　　在 Figures 2 和 Figures 3，我们展示了训练后从  generator net 中提取的样本。

　　　　

　　　　

5 Advantages and disadvantag

　　优点：无需马尔科夫链，仅用反向传播来获得梯度，学习间无需推理，且模型中可融入多种函数。

　　缺点：(论文中说主要为  $p_{g}(x)$  的隐式表示 。且训练时  $\mathrm{G}$  和  $\mathrm{D}$  要同步，即训练  $\mathrm{G}$  后，也要训练  $\mathrm{D} $ ，且不能将 $G$ 训练太好而不去训练 $D$（通俗解释就是 $G$ 训练的太好很容易就"欺骗"了没训练的 $D$）。

　　　　

6 Conclusions

　　相比起卷积神经网络之于计算机视觉，循环神经网络之于自然语言处理，GAN 尚且没有一个特别适合的应用场景。主要原因是 GAN 目前还存在诸多问题。例如：

　　不收敛问题：GAN 是两个神经网络之间的博弈。试想，如果判别器提前学到了非常强的，那么生成器很容易出现梯度消失而无法继续学习。所有 GAN 的收敛性一直是个问题，这样也导致 GAN 在实际搭建过程中对各种超参数都非常敏感，需要精心设计才能完成一次训练任务；

　　崩溃问题：GAN 模型被定义为一个极小极大问题，可以说，GAN 没有一个清晰的目标函数。这样会非常容易导致，生成器在学习的过程中开始退化，总是生成相同的样本点，而这也进一步导致判别器总是被喂给相同的样本点而无法继续学习，整个模型崩溃；

　　模型过于自由： 理论上，我们希望 GAN 能够模拟出任意的真实数据分布，但事实上，由于我们没有对模型进行事先建模，再加上「真实分布与生成分布的样本空间并不完全重合」是一个极大概率事件。那么，对于较大的图片，如果像素一旦过多，GAN 就会变得越来越不可控，训练难度非常大。

 

参考：

GAN生成对抗网络

05-生成网络总结（VAE, GAN）

 

修改历史

2022-02-03 创建文章

2022-06-07 修改文章错误内容

 

论文解读目录