NOJ——1624死胡同（胡搞模拟）

• [1624] 死胡同

• 时间限制: 1000 ms　内存限制: 65535 K
• 问题描述
• 一个死胡同由排成一列的 n 个格子组成，编号从 1 到 n 。
  实验室的“猪猪”一开始在1号格子，开始向前走，每步一格，并且每走 k 步会在当前的格子上打上记号（开始时，1号格子也有记号）。由于这是死胡同，每当“猪猪”走到最左或者最右的格子时，它会改变方向。好奇的“猪猪”在想：如果我一直走，能否把所有格子都打上记号呢？
  

  聪明的你一定知道答案！

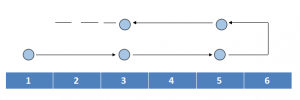
  Hint1：如果 n=6，k=2，位置变化为：1 -> 3 -> 5 -> 5 -> 3 -> 1 -> 3 -> 5 .... 显然，此时不能将所有格子打上标记。(如下图）

  

• 输入
• 多组输入数据（组数<=100）
  每组数据一行，包含两个正整数 n 和 k。
  （1 <= n <= 100000 , 1 <= k <= 100000）
• 输出
• 对于每组数据输出一行 YES 或者 NO 代表能否给所有格子打上标记。
• 样例输入

• 6 2
  6 3

• 样例输出

• NO
  YES

• 提示

• 无

• 来源

• 2015苏州大学ACM-ICPC集训队选拔赛（1）

此题在上学期做过，当时比较naive也是想模拟思路是到头了用reverse数组反转过来再走，然后就机智地TLE了。突然想回来做做这题，当然还是模拟，思路是到头了继续走至超出范围，然后将当前pos对称回来，有种折叠的感觉...事实证明方法可行，但是一交TLE，10W的循环量怎么会TLE?然后找半天找到了几组数据：4 99999，类似于这种k很大n很小的情况下。while里面的while会循环巨多次，此时估计数据量上千万甚至更高然后咋办呢，就开一个结构体数组记录这个点向左走和向右走时是否经过这个点。假设一个点向左走次数或向右走的次数大于等于2，那么这个点在对应的方向被经过了至少两次，可以判断这组数据是走不出来的——只有走不出来的数组才会在某个点重复走来走去。否则让它循环完。

最后膜拜一下那个0ms代码长度还只有300+的。估计是数学方法吧，吾等智商不够又懒...强行模拟好了

代码：

#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<sstream>
#include<cstring>
#include<cstdio>
#include<string>
#include<deque>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
typedef long long LL;
#define INF 0x3f3f3f3f
struct info
{
	int a;
	int b;
};
info pos[100010];
int main(void)
{
	int n,k,i,res;
	while (~scanf("%d%d",&n,&k))
	{
		memset(pos,0,sizeof(pos));
		if(k==1||n==1)//特判
		{
			puts("YES");
			continue;
		}	
		int moni=0;//模拟循环量
		bool flag=0;
		int chushi=1;//初始位置
		int cheng=1;//向左/右走
		int cnt=0;//走过的路个数（不重复）
		while (moni<=100010)
		{			
			chushi+=cheng*k;
			while(chushi>n||chushi<1)
			{
				if(chushi>n)
				{	
					cheng=-1;			
					chushi=n-(chushi-n);										
				}	
				if(chushi<1)
				{
					cheng=1;
					chushi=2-chushi;					
				}	
			}
			if(pos[chushi].a>=2||pos[chushi].b>=2)//重复走过，标记后break
			{
				flag=0;
				break;
			}
			if(cheng==1)//继续正着走
			{
				if(pos[chushi].a==0)
				{
					cnt++;					
				}
				pos[chushi].a++;					
			}
			else//反着走
			{
				if(pos[chushi].b==0)
				{
					cnt++;			
				}
				pos[chushi].b++;
			}				
			if(cnt==n)//模拟量到达，break
			{
				flag=1;
				break;
			}			
			moni++;			
		}
		if(flag)
		{
			puts("YES");
		}
		else
		{
			puts("NO");
		}
	}
	return 0;
}