图的遍历和树的遍历类似。图的遍历是指从图中的某个顶点出发,对图中的所有顶点访问且仅访问一次的过程。通常有两种遍历次序方案:深度优先遍历和广度优先遍历。
一、深度优先遍历
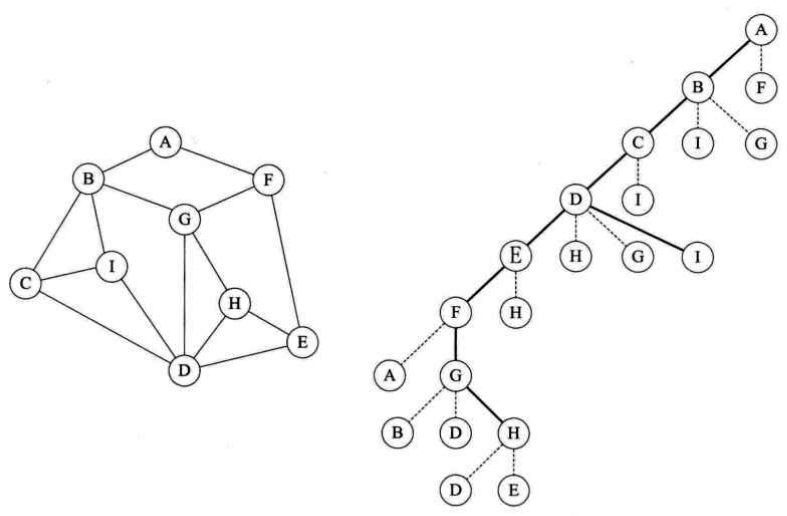
深度优先遍历(Depth_First_Search),也称为深度优先搜索,简称为DFS。深度优先遍历类似于树的前序遍历。
DFS算法描述:从图的某个顶点v开始访问,然后访问它的任意一个邻接点w1,;再从w1出发,访问与w1邻接但未被访问过的顶点w2;然后从w2出发,进行类似访问,如此进行下去,直至所有邻接点都被访问过为止。接着,退回一步,退回到前一次刚访问过的顶点,看是否还有其他未被访问过的邻接点。如果有,则访问此顶点,之后再从此顶点出发,进行与前述类似的访问。重复上述过程,直到连通图中所有顶点都被访问过为止。
二、广度优先遍历
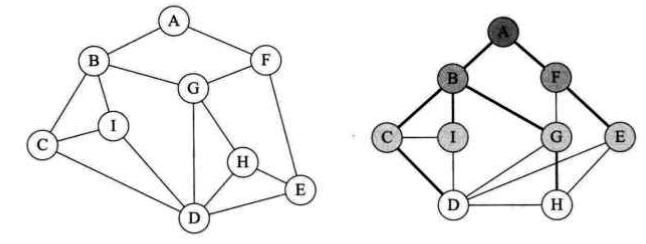
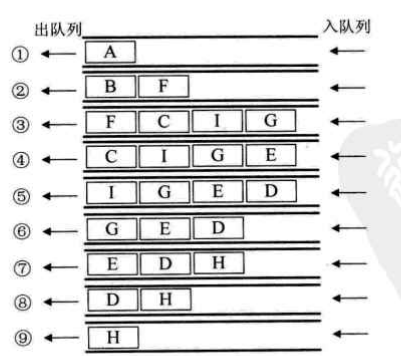
广度优先遍历(Breadth_First_Search),又称为广度优先搜索,简称BFS。图的广度优先遍历类似于树的层序遍历。
BFS算法描述:从图中的某个顶点v开始,先访问该顶点,再依次访问该顶点的每一个未被访问过的邻接点w1,w2,...;然后按此顺序访问顶点w1,w2...的各个还未 被访问过的邻接点。重复上述过程,直到图中的所有顶点都被访问过为止。
以下面的例子为例,深度优先遍历的顶点访问序列为:{A B C D E F G H I};广度优先遍历的顶点访问序列为:{A B F C I G E D H}
三、图的遍历算法实现
1.深度优先遍历
(1)C语言实现
/* 邻接矩阵的深度优先递归算法 */ void DFS(MGraph G, int i) { int j; visited[i] = TRUE; printf("%c ", G.vexs[i]);/* 打印顶点,也可以其它操作 */ for(j = 0; j < G.numVertexes; j++) if(G.arc[i][j] == 1 && !visited[j]) DFS(G, j);/* 对为访问的邻接顶点递归调用 */ } /* 邻接矩阵的深度遍历操作 */ void DFSTraverse(MGraph G) { int i; for(i = 0; i < G.numVertexes; i++) visited[i] = FALSE; /* 初始所有顶点状态都是未访问过状态 */ for(i = 0; i < G.numVertexes; i++) if(!visited[i]) /* 对未访问过的顶点调用DFS,若是连通图,只会执行一次 */ DFS(G, i); }
(2)Java语言实现
package bigjun.iplab.adjacencyMatrix; public class Depth_First_Search { private static boolean[] visited; // 访问标识数组 public static void DFSTraverse(AdjacencyMatrixGraphINF G) throws Exception{ System.out.print("图的深度优先遍历序列为: "); visited = new boolean[G.getVexNum()]; for (int v = 0; v < G.getVexNum(); v++) // 访问标志数组初始化都为false,即未访问过 visited[v] = false; for (int v = 0; v < G.getVexNum(); v++) // 如果没有访问过就对顶点调用深度优先遍历算法 if (!visited[v]) DFS(G, v); System.out.println(); } private static void DFS(AdjacencyMatrixGraphINF G, int v) throws Exception { visited[v] = true; // 先将访问标识数组置为true System.out.print(G.getVex(v).toString() + " "); for (int w = G.firstAdjvex(v); w >= 0; w = G.nextAdjvex(v, w)) if (!visited[w]) DFS(G, w); } }
2.广度优先遍历
(1)C语言实现
Boolean visited[MAXSIZE]; /* 访问标志的数组 */ /* 邻接表的深度优先递归算法 */ void DFS(GraphAdjList GL, int i) { EdgeNode *p; visited[i] = TRUE; printf("%c ",GL->adjList[i].data);/* 打印顶点,也可以其它操作 */ p = GL->adjList[i].firstedge; while(p) { if(!visited[p->adjvex]) DFS(GL, p->adjvex);/* 对为访问的邻接顶点递归调用 */ p = p->next; } } /* 邻接表的深度遍历操作 */ void DFSTraverse(GraphAdjList GL) { int i; for(i = 0; i < GL->numVertexes; i++) visited[i] = FALSE; /* 初始所有顶点状态都是未访问过状态 */ for(i = 0; i < GL->numVertexes; i++) if(!visited[i]) /* 对未访问过的顶点调用DFS,若是连通图,只会执行一次 */ DFS(GL, i); }
(2)Java语言实现
package bigjun.iplab.adjacencyMatrix; import bigjun.iplab.linkQueue.LinkQueue; public class Breadth_First_Search { private static boolean[] visited; public static void BFSTraverse(AdjacencyMatrixGraphINF G) throws Exception{ System.out.print("图的广度优先遍历序列为: "); visited = new boolean[G.getVexNum()]; for (int v = 0; v < G.getVexNum(); v++) // 访问标志数组初始化都为false,即未访问过 visited[v] = false; for (int v = 0; v < G.getVexNum(); v++) // 如果没有访问过就对顶点调用深度优先遍历算法 if (!visited[v]) BFS(G, v); System.out.println(); } private static void BFS(AdjacencyMatrixGraphINF G, int v) throws Exception { visited[v] = true; // 先将访问标识数组置为true System.out.print(G.getVex(v).toString() + " "); // 然后访问对应数组下标的顶点 LinkQueue queue = new LinkQueue(); // 链队列初始化 queue.queueEnter(v); // 将访问过的顶点的数组下标入队列 while (!queue.isqueueEmpty()) { int u = (Integer) queue.queuePoll(); // 队列队头元素出队列并赋值给u for (int w = G.firstAdjvex(u); w >= 0; w = G.nextAdjvex(u, w)) { if (!visited[w]) { visited[w] = true; System.out.print(G.getVex(w).toString() + " "); queue.queueEnter(w); } } } } }
四、(举例)邻接矩阵的深度优先遍历和广度优先遍历
// 手动创建一个无向图 public static AdjacencyMatrixGraphINF createUDGByYourHand() { Object vexs_UDG[] = {"A", "B", "C", "D", "E", "F", "G", "H", "I"}; int[][] arcs_UDG = new int[vexs_UDG.length][vexs_UDG.length]; for (int i = 0; i < vexs_UDG.length; i++) // 构造无向图邻接矩阵 for (int j = 0; j < vexs_UDG.length; j++) arcs_UDG[i][j] = 0; arcs_UDG[0][1] = 1; arcs_UDG[0][5] = 1; arcs_UDG[1][2] = 1; arcs_UDG[1][6] = 1; arcs_UDG[1][8] = 1; arcs_UDG[2][3] = 1; arcs_UDG[2][8] = 1; arcs_UDG[3][4] = 1; arcs_UDG[3][6] = 1; arcs_UDG[3][7] = 1; arcs_UDG[3][8] = 1; arcs_UDG[4][5] = 1; arcs_UDG[4][7] = 1; arcs_UDG[5][6] = 1; for (int i = 0; i < vexs_UDG.length; i++) // 构造无向图邻接矩阵 for (int j = i; j < vexs_UDG.length; j++) arcs_UDG[j][i] = arcs_UDG[i][j]; return new AdjMatGraph(GraphKind.UDG, vexs_UDG.length, 14, vexs_UDG, arcs_UDG); } public static void main(String[] args) throws Exception { AdjMatGraph DNG_Graph = (AdjMatGraph) createUDGByYourHand(); Depth_First_Search.DFSTraverse(DNG_Graph); Breadth_First_Search.BFSTraverse(DNG_Graph); } 输出为: 图的深度优先遍历序列为: A B C D E F G H I 图的广度优先遍历序列为: A B F C G I E D H
五、(举例)邻接表的深度优先遍历和广度优先遍历
public static void main(String[] args) throws Exception { AdjListGraph aListGraph = new AdjListGraph(); aListGraph.createGraph(); System.out.println("该类型的图已经创建完成!"); System.out.println("顶点数组下标为2的第一个邻接点的数组下标是: " + aListGraph.firstAdjvex(2)); int numOfV2 = aListGraph.firstAdjvex(2); System.out.println("顶点V2的第一个邻接点是: " + aListGraph.getVex(numOfV2)); System.out.println("顶点数组下标为2的相对于顶点数组下标为0的下一个邻接点的数组下标是: " + aListGraph.nextAdjvex(2, 0)); int numOfV2toV0next = aListGraph.nextAdjvex(2, 0); System.out.println("顶点V2相对于V0的邻接点是: " + aListGraph.getVex(numOfV2toV0next)); Depth_First_Search.DFSTraverse(aListGraph); Breadth_First_Search.BFSTraverse(aListGraph); } 输出为: 请输入图的类型代号(UDG(无向图)、DG(有向图)、UDN(无向网)、DN(有向网)): UDG 请分别输入图的顶点数,图的边数: 5 6 请分别输入图的各个顶点: V0 V1 V2 V3 V4 请输入各个边的两个顶点(第一个输入是弧尾,第二个输入是弧头): V0 V4 V1 V2 V1 V0 V2 V3 V2 V0 V3 V4 该类型的图已经创建完成! 顶点数组下标为2的第一个邻接点的数组下标是: 0 顶点V2的第一个邻接点是: V0 顶点数组下标为2的相对于顶点数组下标为0的下一个邻接点的数组下标是: 3 顶点V2相对于V0的邻接点是: V3 图的深度优先遍历序列为: V0 V2 V3 V4 V1 图的广度优先遍历序列为: V0 V2 V1 V4 V3