Solution:
注意:基环树的直径是要求不经过重复点和重复边的简单路径。
先把基环树给这样画出来:
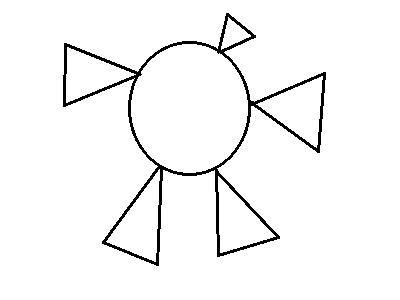
容易想到基环树的直径应在一下情况中取max:
<1>、不经过环上的边,如下:
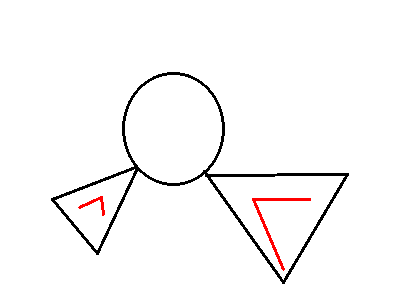
<2>、经过环上一段,并加上两端点各自所在子树中的一段,如下:
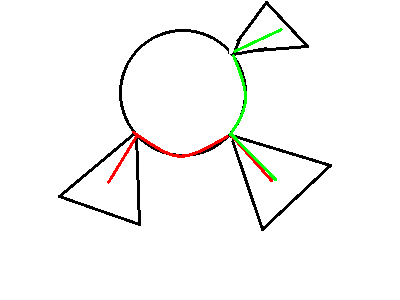
对于第一种情况,可以分别对环上每个点为根的子树求直径。
同时,处理出第二种情况需要的:环上各点到各自子树中的点的最远的距离,记为D。
然后我们相当于需要:
对于环上任意两点i,j,他们在环上距离为dist(i,j),(取顺逆更长)
最大化D[i]+D[j]+dist(i,j)。
由于是环上问题,我们可以断环为链,在结尾倍长一下,就可以把顺逆给包含进去。
这个时候,由于距离可以用前缀和之差表示,我们便可以用单调队列维护区间最值。
#include<string>
#include<cstdio>
#include<cstring>
#define RG register
#define IL inline
#define LL long long
#define DB double
using namespace std;
IL int gi() {
char ch=getchar(); RG int x=0,w=0;
while (ch<'0'||ch>'9') {if (ch=='-') w=1;ch=getchar();}
while (ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
return w?-x:x;
}
const int N=1e6+10;
LL Mx,ans,SUM,D[N],dis[N],pos[N<<1];
int n,H,T,now,cnt,tot,head[N],q[N<<1],Ne[N],Ve[N],fa[N],vis[N],cir[N],dot[N<<1];
struct EDGE{int next,to,v;}e[N<<1];
IL void make(int x,int y,int z) {
e[++tot]=(EDGE){head[x],y,z},head[x]=tot;
e[++tot]=(EDGE){head[y],x,z},head[y]=tot;
}
IL void getcir(int ss) {
RG int x=ss,y;
vis[x]=1;
while (1) {
if (vis[y=Ne[x]]) {
while (x!=y) cir[x]=1,dot[++cnt]=x,pos[cnt]=Ve[x],x=fa[x];
cir[y]=1,dot[++cnt]=y,pos[cnt]=Ve[y];
break;
}
else vis[y]=1,fa[y]=x;
x=y;
}
}
void getdis(int x,int fx,int PaPa) {
RG int i,y;
for (i=head[x],vis[x]=1;i;i=e[i].next)
if ((y=e[i].to)!=fx&&(!cir[y]||y==PaPa))
dis[y]=dis[x]+e[i].v,getdis(y,x,PaPa);
if (Mx<dis[x]) Mx=dis[x],now=x;
}
IL LL getD(int x) {
Mx=0,now=0,getdis(x,0,0),D[x]=Mx;
Mx=0,dis[now]=0,getdis(now,0,x);
return Mx;
}
int main()
{
RG int i,j;
for (i=1,n=gi();i<=n;++i)
Ne[i]=gi(),Ve[i]=gi(),make(i,Ne[i],Ve[i]);
for (i=1;i<=n;++i)
if (!vis[i]) {
cnt=0,ans=0,H=1,T=0,getcir(i);
for (j=1;j<=cnt;++j) ans=max(ans,getD(dot[j]));
for (j=1;j<=cnt;++j) dot[cnt+j]=dot[j];
for (j=1;j<=cnt*2;++j) {
if (j<=cnt) pos[j]+=pos[j-1];
else pos[j]=pos[j-1]+Ve[dot[j]];
if (H<=T&&D[dot[j]]+pos[j]+D[dot[q[H]]]-pos[q[H]]>ans)
ans=D[dot[j]]+pos[j]+D[dot[q[H]]]-pos[q[H]];
while (H<=T&&D[dot[j]]-pos[j]>=D[dot[q[T]]]-pos[q[T]]) --T;
q[++T]=j;
while (H<=T&&j-q[H]+1>=cnt) ++H;
}
SUM+=ans;
}
printf("%lld
",SUM);
return 0;
}
细节也有些要注意的吧。(其实就是我太弱了)