二分搜索总结

时间复杂度：

1）每次用O(1)的时间，将规模为n的问题变为n/2，则总时间复杂度为O(logn).

2）每次用O(n)的时间，将规模为n的问题变为n/2，则总时间复杂度为O(n).

因为T(n) = T(n/2) + O(n) = T(n/4) + O(n/2) + O(n) = .... = T(1) + O(2) + O(4) + ... + O(n/2) + O(n) 约等于 O(n)

2 + 4 + 8 +..+ n/2 + n = 2n-2

由时间复杂度可以反推会用到的算法：

 一. 找数组中第一个/最后一个 满足某个条件的位置：

1. 第一次出现的下标：

思路：使用二分法逐渐把范围缩小，最后start和end指向两个相邻的元素。再进行double check。

class Solution {
public:
    /**
     * @param nums: The integer array.
     * @param target: Target to find.
     * @return: The first position of target. Position starts from 0.
     */
    int binarySearch(vector<int> &nums, int target) {
        // write your code here
        if(nums.empty())
            return -1;   //target不存在数组中，返回-1
        int start = 0, end = nums.size()-1;
        
        //相邻就退出循环
        // start = 1, end = 2 就要退出
        while(start + 1 < end){
            int mid = start + (end-start)/2;
            if(target == nums[mid])
                end = mid;
            else if(target < nums[mid])
            //也可写成 end = mid-1;
                end = mid;
            else
            //或 start = mid+1;
                start = mid;
        }
        //double check
        if(nums[start] == target)
            return start;
        if(nums[end] == target)
            return end;
        //未找到    
        return -1;
    }
};

2. 最后一次出现的下标：

 

 注意while循环的判断条件一定要写成：

start+1 < end

因为写成start<end时会导致死循环。并注意在double check时，要先check nums[end], 再check nums[start]， 因为是找最后一个满足条件的。

class Solution {
public:
    /**
     * @param nums: An integer array sorted in ascending order
     * @param target: An integer
     * @return: An integer
     */
    int lastPosition(vector<int> &nums, int target) {
        // write your code here
        //start<end => dead loop
        //e.g. [2,2], target = 2, mid=(0+1)/2=0
        //then start = mid = 0, always < end
        if(nums.empty())
            return -1;
        int start = 0, end = nums.size()-1;
        while(start+1 < end){
            int mid = start + (end-start)/2;
            if(nums[mid] == target)
                start = mid;
            else if(target > nums[mid])
                start = mid;
            else
                end = mid;
        }
        if(nums[end] == target)
            return end;
        if(nums[start] == target)
            return start;
        return -1;
    }
};

 3. 找到某个数在数组中出现的坐标区间：

注意 if else 要写全...

class Solution {
public:
    /**
     * @param A: an integer sorted array
     * @param target: an integer to be inserted
     * @return: a list of length 2, [index1, index2]
     */
    vector<int> searchRange(vector<int> &A, int target) {
        // write your code here
        int n = A.size();
        vector<int> res(2, -1);
        if(A.empty())
            return res;
        
        int start = 0, end = n-1;
        while(start+1<end){
            int mid = start + (end-start)/2;
            if(A[mid] == target)
                end = mid;  //找target的起始坐标
            else if(target < A[mid])
                end = mid;
            else
                start = mid;
        }
        if(A[start] == target)
            res[0] = start;
        else if(A[end] == target)
            res[0] = end;
        
        start = 0, end = n-1;
        while(start+1<end){
            int mid = start + (end-start)/2;
            if(A[mid] == target)
                start = mid;  //找target的结尾坐标
            else if(target < A[mid])
                end = mid;
            else
                start = mid;
        }
        if(A[end] == target)
            res[1] = end;
        else if(A[start] == target)
            res[1] = start;
        
        return res;
    }
};

  

3. 找到target在数组中插入的位置：即如果找到相等的值就插入到这个值所在的索引；找到第一个比target大的值，就插入到这个值的位置上，代码是找到最后一个比target小的位置，然后将target插入到这个位置+1处。

class Solution {
public:
    /**
     * @param A: an integer sorted array
     * @param target: an integer to be inserted
     * @return: An integer
     */
    int searchInsert(vector<int> &A, int target) {
        // write your code here
        //找到第一个大于等于target的位置
        if(A.empty())
            return 0;
        if(target<A[0])
            return 0;
            
        int start = 0, end = A.size()-1;
        //找到最后一个小于等于target的位置
        while(start+1 < end){
            int mid = start + (end-start)/2;
            if(A[mid] == target)
                return mid;
            else if(target < A[mid])
                end = mid;
            else 
                start = mid;
        }
        if(A[end] == target)
            return end;
        else if(A[end] < target)
            return end+1;
        if(A[start] == target)
            return start;
        else if(A[start] < target)
            return start+1;
    }
};

二分法：

class Solution {
public:
    /**
     * @param matrix: matrix, a list of lists of integers
     * @param target: An integer
     * @return: a boolean, indicate whether matrix contains target
     */
    bool searchMatrix(vector<vector<int>> &matrix, int target) {
        // write your code here
        if(matrix.empty() || matrix[0].empty())
            return false;
        int n = matrix.size(), m = matrix[0].size();
        int start = 0, end = n*m-1;
        int rol=0, col = 0;
        while(start+1 < end){
            int mid = start + (end-start)/2;
            rol= mid/m, col = mid%m;
            if(matrix[rol][col] == target)
                return true;
            else if(target < matrix[rol][col])
                end = mid;
            else
                start = mid;
        }
        
        if(matrix[start/m][start%m] == target || matrix[end/m][end%m] == target)
            return true;
        return false;
    }
    
};

思路：从矩阵的左下角出发，每次去掉一行或一列，因为是统计矩阵中等于target的次数，所以遇到相等的数值，需要将res+1，然后再将i-1和j+1继续寻找。

class Solution {
public:
    /**
     * @param matrix: A list of lists of integers
     * @param target: An integer you want to search in matrix
     * @return: An integer indicate the total occurrence of target in the given matrix
     */
    int searchMatrix(vector<vector<int>> &matrix, int target) {
        // write your code here
        //从左下角出发，每次删除一行或一列
        if(matrix.empty() || matrix[0].empty())
            return 0;
        int n = matrix.size(), m = matrix[0].size();
        int res = 0;
        int i=n-1, j = 0;
        while(i>=0 && j<=m-1){
            if(matrix[i][j] == target){
                res ++;
                i--;
                j++;
            }
                
            else if(target < matrix[i][j]){
                i--;
            }
            else 
                j++;
        }
        return res;
    }
};

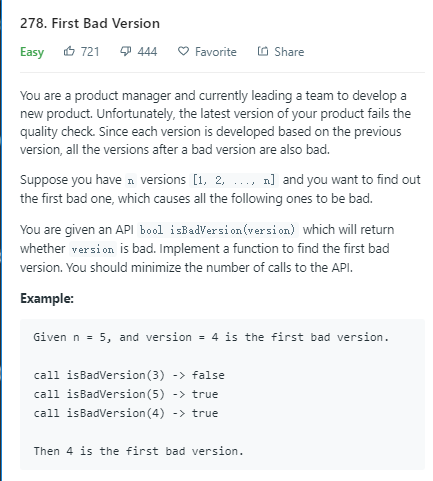
// Forward declaration of isBadVersion API.
bool isBadVersion(int version);

class Solution {
public:
    int firstBadVersion(int n) {
        //找到第一个bad version
        int start = 0, end = n;
        while(start+1 < end){
            int mid = start + (end-start)/2;
            if(isBadVersion(mid))
                end = mid;
            else
                start = mid;
        }
        if(isBadVersion(start))
            return start;
        return end;
    }
};

class Solution {
public:
    int peakIndexInMountainArray(vector<int>& A) {
        int start = 0, end = A.size()-1;
        while(start+1 < end){
            int mid = start + (end-start)/2;
            if(A[mid] < A[mid+1])
                start = mid;
            else
                end = mid;
        }
        if(A[start]>A[end])
            return start;
        else
            return end;
    }
};

进阶版：

解法一：O(n) 线性扫描一遍。每次只需要比较

 nums[i]>nums[i+1]

分三种情况：

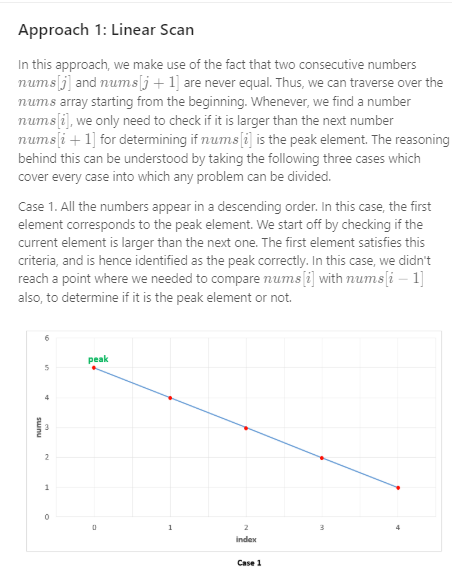
 第二种情况是递增的数组，最后返回的是数组的最后一个元素，即nums.size()-1

 

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int n = nums.size();
        for(int i=0; i<n-1; i++){
             if(nums[i]>nums[i+1])
                 return i;
         }
        return n-1;
    }
};

解法二：二分法

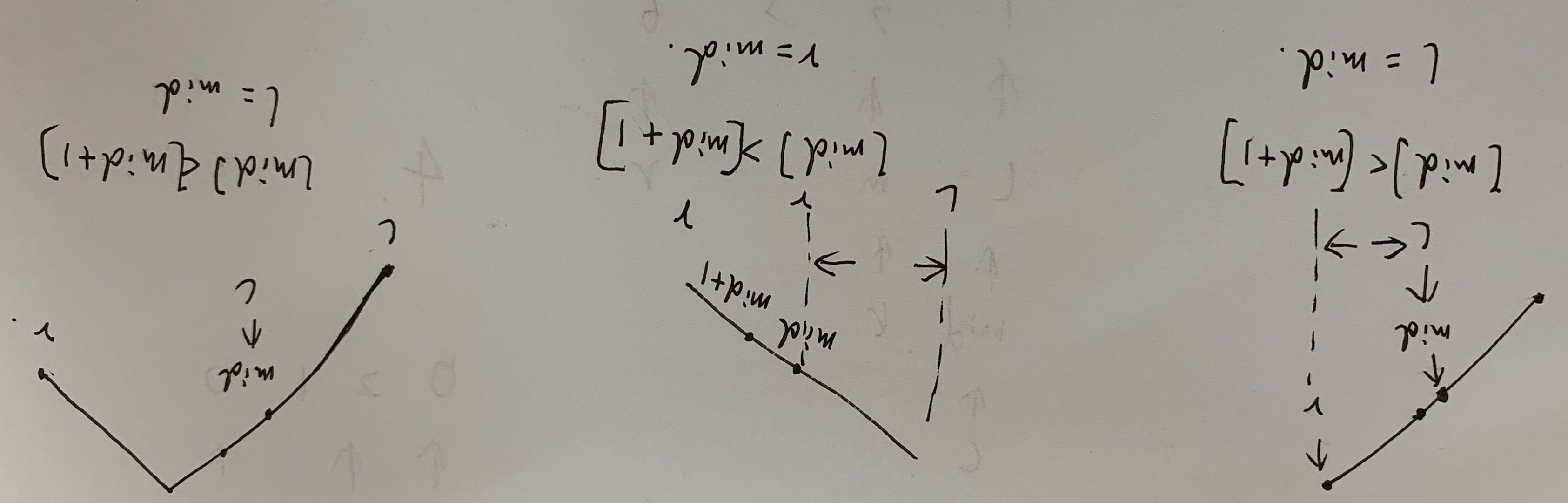
class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int start = 0, stop = nums.size()-1;
        while(start+1 < stop){
            int mid = start + (stop-start)/2;
            if(nums[mid] < nums[mid+1])
                start = mid;
            else
                stop = mid;
        }
        if(nums[start]>nums[stop])
            return start;
        else
            return stop;
    }
};

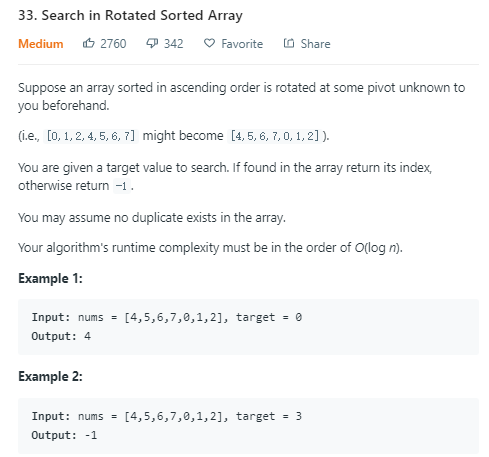
二分法：可以将这个旋转数组看作两段递增的数组，然后多加一层判断。

class Solution {
public:
    int search(vector<int>& nums, int target) {
        if(nums.empty())
            return -1;
        int start = 0, end = nums.size()-1;
        while(start+1 < end){
            int mid = start + (end-start)/2;
            if(nums[mid] == target)
                return mid;
            if(nums[start] < nums[mid]){
                //在左半段
                if(target >= nums[start] && target <= nums[mid])
                    end = mid;
                else
                    start = mid;
            }
            else{
                //在右半段
                if(target >= nums[mid] && target <= nums[end])
                    start = mid;
                else
                    end = mid;
            }
        }
        if(nums[start] == target)
            return start;
        else if(nums[end] == target)
            return end;
        return -1;
    }
};

进阶版：旋转数组中有重复元素，时间复杂度只能是O(n)。

class Solution {
public:
    bool search(vector<int>& nums, int target) {
        if(nums.empty())
            return false;
        int start = 0, end = nums.size()-1;
        while(start + 1 < end){
            int mid = start + (end-start)/2 ;
            if(nums[mid] == target)
                return true;
            if(nums[start] < nums[mid]){
                if(target<=nums[mid] && target>= nums[start])
                    end = mid;
                else
                    start = mid;
            }
            else if(nums[start] > nums[mid]){
                if(target>=nums[mid] && target<=nums[end])
                    start= mid;
                else
                    end = mid;
            }
            else 
                //nums[start] > nums[mid]
                start ++ ;
        }
        if(nums[start] == target || nums[end] == target)
            return true;
        return false;
    }
};

 

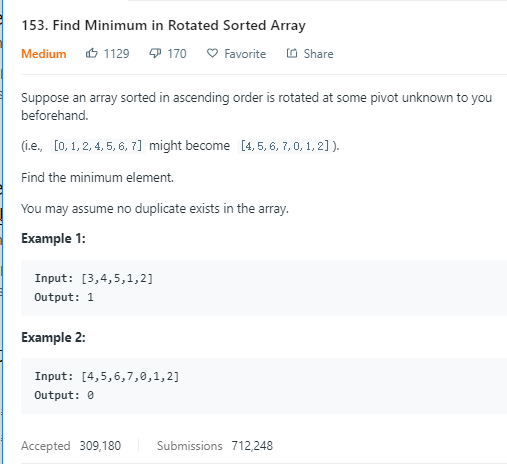
参考思路：https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/solution/

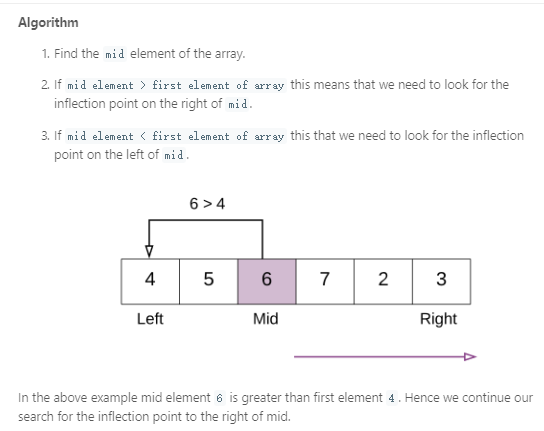
class Solution {
public:
    int findMin(vector<int>& nums) {
        if(nums.size()==1)
            return nums[0];
        
        int start = 0, end = nums.size()-1;
        if(nums[end] > nums[0])
            //说明没有反转，本身是一个排序好的数组
            return nums[0];
        
        while(start + 1 < end){
            int mid = start + (end-start)/2 ;
            if(nums[mid] < nums[mid-1])
                return nums[mid];
            if(nums[mid] > nums[mid+1])
                return nums[mid+1];
            if(nums[mid] > nums[0])
                start = mid;
            else
                end = mid;
        
        }
        if(nums[start]>nums[end])
            return nums[end];
        else
            return nums[start];
 
    }
};

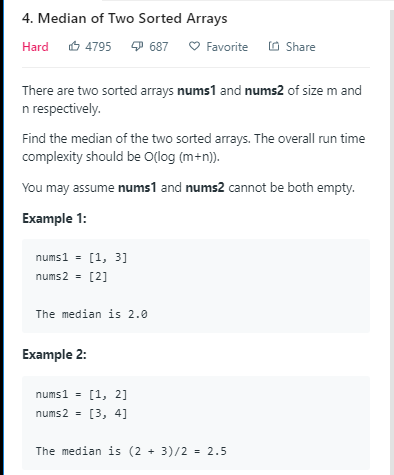
二分+分治：

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int len = nums1.size() + nums2.size();
        if(len % 2 == 0)
            //长度为偶数 中位数为中间两个数的平均值
            return (findKth(nums1, 0, nums2, 0, len/2) + findKth(nums1, 0, nums2, 0, len/2 +1))/2.0;
        else
            return findKth(nums1, 0, nums2, 0, len/2 +1);
    }
    int findKth(vector<int>& n1, int start1, vector<int>& n2, int start2, int k){
        //递归终止条件
        if(start1 >= n1.size())
            return n2[start2 + k -1];
        if(start2 >= n2.size())
            return n1[start1 + k -1];
        if(k==1)
            return min(n1[start1], n2[start2]);
        
        //若k/2的长度不在nums1中，则将其k/2处设为最大值，表示只会删掉/挪动start2的start2指针
        //取n1的第k/2个数
        int halfK1 = start1 + k/2 -1 < n1.size() ? n1[start1 + k/2 -1] : INT_MAX;
        //取n2的第k/2个数
        int halfK2 = start2 + k/2 -1 < n2.size() ? n2[start2 + k/2 -1] : INT_MAX;
        
        if(halfK1 < halfK2)
            return findKth(n1, start1 + k/2, n2, start2, k - k/2);
        else
            return findKth(n1, start1, n2, start2 + k/2, k- k/2);
    }
    
};

思路：三步翻转法：先把前一段翻转，再把后一段翻转，再把整个数组翻转。

class Solution {
public:
    /**
     * @param nums: An integer array
     * @return: nothing
     */
    void recoverRotatedSortedArray(vector<int> &nums) {
        // write your code here
        
        for(int i=0; i<nums.size()-1; i++){
            if(nums[i] > nums[i+1]){
                //找到一个比后面一位大的数
                reverse(nums.begin(), nums.begin()+i+1);  //reverse是左闭右开区间
                reverse(nums.begin()+i+1, nums.end());
                reverse(nums.begin(), nums.end());
            }
        }
    }
};

class Solution {
public:
    /**
     * @param str: An array of char
     * @param offset: An integer
     * @return: nothing
     */
    void rotateString(string &str, int offset) {
        // write your code here
        int n = str.size();
        if(n==0)
            return;
        offset %= n;
        reverse(str.begin(), str.begin()+n-offset);
        reverse(str.begin()+n-offset, str.end());
        reverse(str.begin(), str.end());
    }
};

class Solution {
public:
    /**
     * @param str: An array of char
     * @param offset: An integer
     * @return: nothing
     */
    void rotateString(string &str, int offset) {
        // write your code here
        int n = str.size();
        if(n==0)
            return;
        offset %= n;
        str = str.substr(n-offset, offset) + str.substr(0, n-offset);  //substr(pos, len)
    }
};

使用O(1)的空间复杂度，思路：先将整个字符串s翻转，处理掉首尾的空格后，再将每个单词翻转，再处理中间的冗余空格。

class Solution {
public:
    string reverseWords(string s) {
        //先整体翻转，再逐个单词翻转,需要处理首尾及中间冗余空格
        reverse(s.begin(), s.end());
        int n = s.size();
        int start=0, end = n-1;
        //首空格
        while(start<n && s[start]==' ')
            start++;
        //尾空格
        while(end>=0 && s[end]==' ')
            end--;
        //特殊情况
        if(start > end)
            return "";
        
        //逐个单词翻转
        for(int i=start; i<=end; ){
            while(s[i]==' ' && i<=end)
                i++;
            int l = i;
            while(s[l]!=' ' && l<=end)
                l++;
            reverse(s.begin()+i, s.begin()+l);
            i = l;
        }
        
        //处理中间冗余空格
        int tail = start;
        for(int i=start; i<=end; i++){
            if(s[i] == ' ' && s[i-1] == ' ') //去掉重复的空格
                continue;
            s[tail++] = s[i];
        }
        
        return s.substr(start, tail-start);  //s.substr(pos, len)
    }
};

class Solution {
public:
    bool rotateString(string A, string B) {
        //find()函数在找不到指定值得情况下会返回string::npos
        return A.size()==B.size() && (A+A).find(B) != string::npos;  //把两个A字符串拼起来，若在里面找不到B返回false
    }
};