(分治法)leetcode 932. Beautiful Array

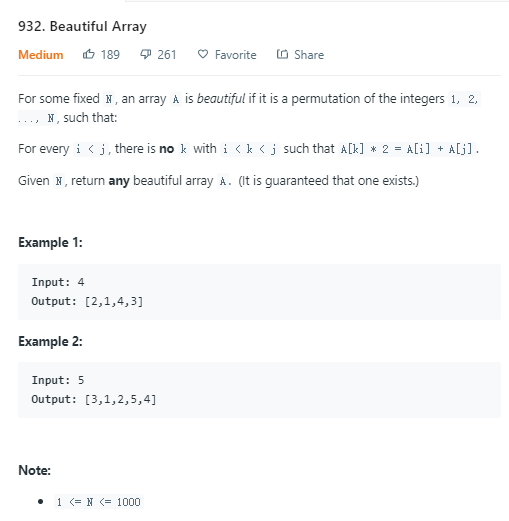
题意：A是一个从1到N的全排列数组，对于每个A里的元素，都不存在 i<k<j 时， A[k]*2 = A[i] * A[j] 

解法一：迭代

C++

class Solution {
public:
    vector<int> beautifulArray(int N) {
        vector<int> res = {1};
        while(res.size()<N){
            vector<int> temp;
            for(auto x: res){
                if(x*2-1<=N)
                    temp.push_back(x*2-1);
            }
            for(auto x: res){
                if(x*2<=N)
                    temp.push_back(x*2);
            }
            //swap(temp, res);
            res = temp;
        }
        return res;
    }
};

Python：

class Solution(object):
    def beautifulArray(self, N):
        """
        :type N: int
        :rtype: List[int]
        """
        res = [1]
        while len(res)<N :
            res = [ i*2-1 for i in res] + [i*2 for i in res];
        
        return [i for i in res if i<=N]

 解法二：递归, 个数为N的序列中，奇数的个数为(N+1)/2, 偶数的个数为N/2，故beautifulArray(N) 由 beautifulArray(N/2) + beautifulArray(N/2)

Python:

class Solution(object):
    def beautifulArray(self, N):
        """
        :type N: int
        :rtype: List[int]
        """
        if(N==1):
            return [1]
        # N为偶 N%2为0；N为奇 N%2为1
        odd = [i*2-1 for i in self.beautifulArray(N/2 + N%2)]
        even = [i*2 for i in self.beautifulArray(N/2)]
        
        return odd+even

C++

class Solution {
public:
    vector<int> beautifulArray(int N) {
        vector<int> res;
        if(N==1){
            res.push_back(1);
            return res;
        }
        vector<int> temp;
        temp = beautifulArray((N+1)/2);
        for(auto a: temp)
            res.push_back(a*2-1);
        temp = beautifulArray(N/2);
        for(auto a:temp)
            res.push_back(a*2);
        
        return res;
    }
};