【数学】【定理】F. Anton and School
思路
\[a+b=a\space xor\space b + a\&b
\]
xor本质上是一种取消进位的模二加法。
而&与运算是一种进位的运算。
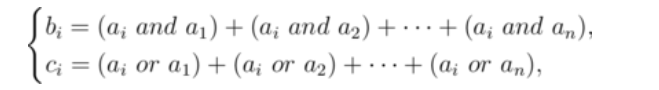
\[a_i\space and\space a_1+a_i\space or\space a_1=a_i+a_1
\]
进而有\(b_i+c_i=na_i+\sum_{i=1}^n a_i\)
进而有\(\sum_{i=1}^{n}b_i+\sum_{i=1}^{n}c_i=2n\sum_{i=1}^{n}a_i\)
进而有\(a_i=\frac{b_i+c_i-\sum_{i=1}^{n}a_i}{n}\)
然后我们就可以算出每一个\(a_i\)了
但分子一旦不能被n整除的话,那么结果的小数位就会被截断(a是整数)。
因而我们还需要进行复原来检查一下是否是对的。
对于如何形成\(b_i\)和\(c_i\),我们可以单独考虑每一位对整体的贡献,将所有贡献加起来就可以更快的算出答案。
(可以分两类,自己和自己进行运算和自己和其他数字进行运算)
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 1000000007
using namespace std;
const int N = 3E5+5,M = 6E5+10;
ll n,m,a[N],b[N],c[N],cnt[35];
ll suma,sumb,sumc;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)
cin>>b[i],sumb += b[i];
for(int i=1;i<=n;i++)
cin>>c[i],sumc += c[i];
suma = (sumb+sumc)/(2*n);
for(int i=1;i<=n;i++)
{
a[i] = (b[i]+c[i]-suma)/n;
for(int j=30;j>=0;j--)
if( (a[i]>>j)&1 ) cnt[j]++;
}
for(int i=1;i<=n;i++)
{
ll tempb = 0 , tempc = 0;
for(int j=30;j>=0;j--)
{
if( (a[i]>>j)&1 )
{
tempb += (1<<j)*(cnt[j]-1);
tempc += (1<<j)*(n-1);
}
else tempc += (1<<j)*cnt[j];
}
tempb += a[i], tempc += a[i];//对本身或运算和与运算等于本身
if(tempb!=b[i]||tempc!=c[i])
{
cout<<-1;
return 0;
}
}
for(int i=1;i<=n;i++)
cout<<a[i]<<" ";
return 0;
}