DP数字三角形变形——方格取数
设有 N×N 的方格图,我们在其中的某些方格中填入正整数,而其它的方格中则放入数字0。如下图所示:
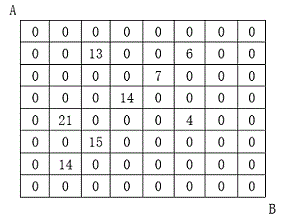
某人从图中的左上角 A 出发,可以向下行走,也可以向右行走,直到到达右下角的 B 点。
在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字0)。
此人从 A 点到 B 点共走了两次,试找出两条这样的路径,使得取得的数字和为最大。
思路:
尽可能减少变量(状态数)来降低空间的使用
原先的四维数组
f[路线一的横坐标][路线一的纵坐标][路线二的横坐标][路线二的纵坐标]
x1+y1=x2+y2=t,t相当于一套换算法则,x1,x2相当于输入的信息,而y1,y2是通过这套换取来的结果。
所以可以建立三维数组来换取空间的优化
f[曼哈顿距离][路线一的横坐标][路线二的横坐标]
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin>>n;
int a[n+1][n+1];
for(int i=0;i<=n+1;i++)
for(int j=0;j<=n+1;j++)
a[i][j]=0;
while(1)
{
int x,y,z;
cin>>x>>y>>z;
if(x==0&&y==0&&z==0)
break;
a[x][y]=z;
}
int f[n+n+10][n+10][n+10];
for(int i=0;i<2*n+5;i++)
{
for(int j=0;j<n+5;j++)
for(int k=0;k<n+5;k++)
f[i][j][k]=0;
}
for(int i=1;i<=2*n-1;i++)
for(int j=1;j<=i;j++)
for(int k=1;k<=i;k++)
{
int add=a[j][i-j+1]+a[k][i-k+1];
if(j==k)
{
add=add-a[j][i-j+1];
}
f[i][j][k]=max(f[i-1][j][k]+add, f[i][j][k]);
f[i][j][k]=max(f[i-1][j-1][k]+add,f[i][j][k]);
f[i][j][k]=max(f[i-1][j][k-1]+add, f[i][j][k]);
f[i][j][k]=max(f[i-1][j-1][k-1]+add, f[i][j][k]);
}
cout<<f[2*n-1][n][n];
return 0;
}