动态树之LCT(link-cut tree)讲解

　　动态树是一类要求维护森林的连通性的题的总称，这类问题要求维护某个点到根的某些数据，支持树的切分，合并，以及对子树的某些操作。其中解决这一问题的某些简化版（不包括对子树的操作）的基础数据结构就是LCT(link-cut tree)。

　　LCT的大体思想类似于树链剖分中的轻重链剖分(轻重链剖分请移步http://www.cnblogs.com/BLADEVIL/p/3479713.html)，轻重链剖分是处理出重链来，由于重链的定义和树链剖分是处理静态树所限，重链不会变化，变化的只是重链上的边或点的权值，由于这个性质，我们用线段树来维护树链剖分中的重链，但是LCT解决的是动态树问题（包含静态树），所以需要用更灵活的splay来维护这里的“重链”(splay请移步http://www.cnblogs.com/BLADEVIL/p/3464458.html)。

定义：

　　首先来定义一些量：

　　access(X)：表示访问X点（之后会有说明）。

　　Preferred child（偏爱子节点）：如果最后被访问的点在X的儿子P节点的子树中，那么称P为X的Preferred child，如果一个点被访问，他的Preferred child为null(即没有)。

　　Preferred edge（偏爱边）：每个点到自己的Preferred child的边被称为Preferred edge。

　　Preferred path（偏爱路径）：由Preferred edge组成的不可延伸的路径称为Preferred path。

这样我们可以发现一些比较显然的性质，每个点在且仅在一条Preferred path上，也就是所有的Preferred path包含了这棵树上的所有的点，这样一颗树就可以由一些Preferred path来表示（类似于轻重链剖分中的重链），我们用splay来维护每个条Preferred path，关键字为深度，也就是每棵splay中的点左子树的深度都比当前点小，右节点的深度都比当前节点

的深度大。这样的每棵splay我们称为Auxiliary tree(辅助树)，每个Auxiliary tree的根节点保存这个Auxiliary tree与上一棵Auxiliary tree中的哪个点相连。这个点称作他的Path parent。

看一个例子

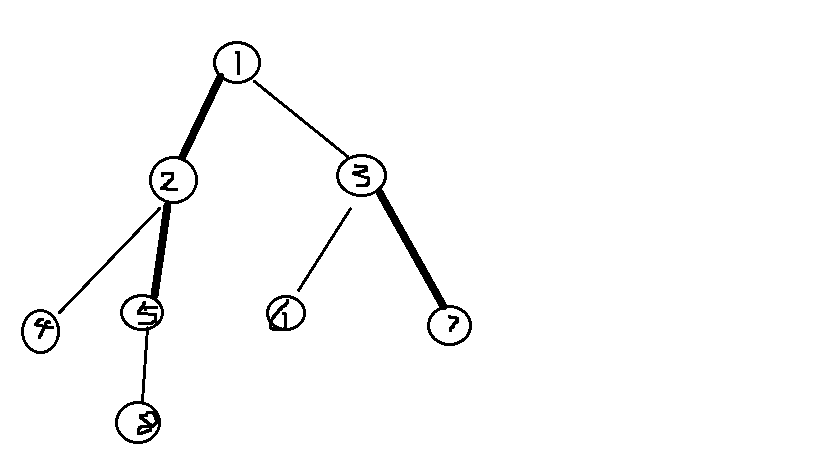
粗的边是Preferred path。那么3-7这个Auxiliary tree中，Path parent为1节点，每个单独的点单独在一棵splay中。以上描述的几个量可以存储这棵树，并且维护相应的信息。

操作：

　　access(X)：首先由于preferred path的定义，如果一个点被访问，那么这个点到根节点的所有的边都会变成preferred edge，由于每个点只有一个preferred child，所以这个点到根节点路径上的所有的点都会和原来的preferred child断开，连接到这条新的preferred path上。假设访问X点，那么先将X点旋转到对应Auxiliary tree的根节点，然后因为被访问的点是没有preferred child的，所以将Auxiliary tree中根节点(X)与右子树的边断掉，左节点保留，将这个树的path parent旋转到对应Auxiliary tree的根节点，断掉右子树，连接这个点与X点，相当于合并两棵Auxiliary tree，不断地重复这一操作，直到当前X所在Auxiliary tree的path parent为null时停止，表示已经完成当前操作。

procedure access(x:longint);
var
    y                    :longint;
begin
    splay(x);//旋转
    while father[x]<>0 do
    begin
        y:=father[x];
        splay(y);
        root[son[y,1]]:=true;//son为子节点son[x,0]代表左子结点，son[x,1]代表右子结点
        root[x]:=false;//当前点是否为对应Auxiliary tree的根节点
        son[y,1]:=x;
        update(y);//更新y点的信息
        splay(x);
    end;
end;

　　find root(x)：找到某一点所在树的根节点（维护森林时使用）。只需要access(X)，然后将X节点旋到对应Auxiliary tree的根节点，然后找到这个Auxiliary tree中最左面的点。

　

function find root(x:longint):longint;
begin
　　access(x);
　　splay(x);//将X旋转到根节点
　　exit(find(x,-maxlongint));//找到子树中最左面的点
end;

　　cut(x)：断掉X节点和其父节点相连的边。首先access(X)，然后将X旋转到对应Auxiliary tree的根节点，然后断掉Auxiliary tree中X和左节点相连的边。

procedure cut(x:longint);
begin
　　access(x);
　　splay(x);//旋转x点到根节点
　　father[son[x,0]]:=0;
　　root[son[x,0]]:=true;//设置左子树根节点
　　son[x,0]:=-1;
end;

　　link(join)(x,y)：连接点x到y点上。即让x称为y的子节点。因为x为y的子节点后，在原x的子树中，x点到根节点的所有的点的深度会被翻转过来，所以先access(x)，然后在对应的Auxiliary tree中将x旋转到根节点，，然后将左子树翻转(splay中的reverse操作)，然后access(y)，将y旋转到对应Auxiliary tree中的根节点，将x连到y就行了。

procedure link(x,y:longint);
begin
　　access(x);
　　splay(x);
　　reverse(son[x,0]);
　　access(y);
　　splay(y);
　　son[y,1]:=x;
　　father[x]:=y;
　　root[x]:=false;
end;

access操作是LCT的基础，应该熟练掌握并且理解。

时间复杂度：

　　证明access以及其他操作的时间复杂度是均摊log₂N的，具体证明参考杨哲的论文《QTREE 解法的一些研究》。

基础题，bzoj 2002:http://61.187.179.132/JudgeOnline/problem.php?id=2002

/**************************************************************
    Problem: 2002
    User: BLADEVIL
    Language: Pascal
    Result: Accepted
    Time:2372 ms
    Memory:4328 kb
****************************************************************/
 
//By BLADEVIL
var
    n, m                :longint;
    father, size        :array[-1..200010] of longint;
    son                 :array[-1..200010,0..2] of longint;
    root                :array[-1..200010] of boolean;
 
procedure update(x:longint);
begin
    size[x]:=size[son[x,0]]+size[son[x,1]]+1;
end;
     
procedure left_rotate(x:longint);
var
    y                   :longint;
begin
    y:=son[x,1];
    son[x,1]:=son[y,0];
    father[son[x,1]]:=x;
    son[y,0]:=x;
    if x=son[father[x],0] then
        son[father[x],0]:=y else
    if x=son[father[x],1] then
        son[father[x],1]:=y;
    father[y]:=father[x];
    father[x]:=y;
    root[y]:=root[x] xor root[y];
    root[x]:=root[x] xor root[y];
    update(x); update(y);
end;
 
procedure right_rotate(x:longint);
var
    y                   :longint;
begin
    y:=son[x,0];
    son[x,0]:=son[y,1];
    father[son[x,0]]:=x;
    son[y,1]:=x;
    if x=son[father[x],0] then
        son[father[x],0]:=y else
    if x=son[father[x],1] then
        son[father[x],1]:=y;
    father[y]:=father[x];
    father[x]:=y;
    root[y]:=root[y] xor root[x];
    root[x]:=root[y] xor root[x];
    update(x); update(y);
end;
     
procedure splay(x:longint);
begin
    while not root[x] do
        if x=son[father[x],1] then
            left_rotate(father[x]) else
            right_rotate(father[x]);
end;
     
procedure access(x:longint);
var
    y                   :longint;
begin
    splay(x);
    while father[x]<>0 do
    begin
        y:=father[x];
        splay(y);
        root[son[y,1]]:=true;
        root[x]:=false;
        son[y,1]:=x;
        update(y);
        splay(x);
    end;
end;
     
procedure init;
var
    i                   :longint;
begin
    read(n);
    for i:=1 to n do
    begin
        read(father[i]);
        father[i]:=father[i]+i;
        if father[i]>n then father[i]:=n+1;
    end;
    read(m);
end;
 
procedure main;
var
    i                   :longint;
    x, y, z             :longint;
begin
    for i:=1 to n+1 do size[i]:=1;
    fillchar(root,sizeof(root),true);
    for i:=1 to m do
    begin
        read(x);
        if x=1 then
        begin
            read(y); inc(y);
            access(y);
            writeln(size[son[y,0]]);
        end else
        begin
            read(y,z); inc(y);
            splay(y);
            father[son[y,0]]:=father[y];
            root[son[y,0]]:=true;
            son[y,0]:=0; 
            size[y]:=size[son[y,1]]+1;
            father[y]:=y+z;
            if father[y]>n then father[y]:=n+1;
        end;
    end;
end;
     
begin
    init;
    main;
end.