切糕
经历千辛万苦小A得到了一块切糕,切糕的形状是长方体,小A打算拦腰将切糕切成两半分给小B。出于美观考虑,小A希望切面能尽量光滑且和谐。于是她找到你,希望你能帮她找出最好的切割方案。
出于简便考虑,我们将切糕视作一个长P,宽Q,高R的长方体点阵。我们将位于第z层中第x行,第y列上的点称为(x,y,z),它有一个非负的不和谐值v(x,y,z)。一个合法的切面满足以下两个条件:
1.与每个纵轴有且仅有一个交点。即切面是一个函数f(x,y),对于所有1≤x≤P,1≤y≤Q,我们需指定一个切割点f(x,y),且 1≤f(x,y)≤R。
2.切面需要一定的光滑性要求,即相邻纵轴上的切割点不能相距太远。对于所有 1≤x,x'≤P 和 1≤y,y'≤Q,若 |x-x'|+|y-y'|=1,则 |f(x,y)-f(x',y')|≤D,其中D是给定的一个非负整数。
可能有许多切面满足上面的条件,小A希望找出总的切割点上的不和谐值最小的那个,即sigma(v(x,y,f(x,y)))最小。
Input
第一行是三个正整数P,Q,R,表示切糕的长P、 宽Q、高R。第二行有一个非负整数D,表示光滑性要求。接下来是R个P行Q列的矩阵,第z个 矩阵的第x行第y列是v(x,y,z) (1≤x≤P, 1≤y≤Q, 1≤z≤R)。
100%的数据满足P,Q,R≤40,0≤D≤R,且给出的所有的不和谐值不超过1000。
Output
仅包含一个整数,表示在合法基础上最小的总不和谐值。
Sample Input
2 2 2
1
6 1
6 1
2 6
2 6
Sample Output
6
Hint
最佳切面的f为f(1,1)=f(2,1)=2,f(1,2)=f(2,2)=1
标签:网络流,最小割
建模神题。
建图:
建r+1层,每层p*q的图,相邻两竖边建模如下
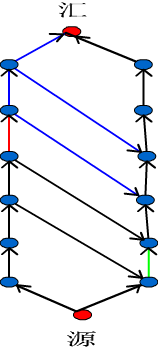
图片转载自Zarxdy34
这样如果割掉红边,右边割的边必须在绿边下面才能有流。所以割的边就限制在绿边上面了。因此这样一来,下界就满足了。
对于上界,右边的几个点反过来同种方式建边(图中只画了左侧的边)
附上AC代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define MAX_A 40
#define MAX_N 70000
#define MAX_M 300000
#define INF 2147483647
using namespace std;
int s, t, id[MAX_A+5][MAX_A+5][MAX_A+5];
int move[2][4] = {{0, 1, 0, -1}, {1, 0, -1, 0}};
struct Edge {int v, c, nxt;} E[MAX_M+5];
int pre[MAX_N+5], d[MAX_N+5], cnt, num;
queue <int> que;
void init() {cnt = num = 0; memset(pre, -1, sizeof(pre));}
void insert(int u, int v, int c) {
E[cnt].v = v, E[cnt].c = c;
E[cnt].nxt = pre[u], pre[u] = cnt++;
E[cnt].v = u, E[cnt].c = 0;
E[cnt].nxt = pre[v], pre[v] = cnt++;
}
bool BFS() {
memset(d, -1, sizeof(d));
while (!que.empty()) que.pop();
d[s] = 0, que.push(s);
while (!que.empty()) {
int u = que.front();
for (int i = pre[u]; i != -1; i = E[i].nxt)
if (E[i].c && d[E[i].v] == -1)
d[E[i].v] = d[u]+1, que.push(E[i].v);
que.pop();
}
return d[t] != -1;
}
int DFS(int u, int flow) {
if (u == t) return flow;
int ret = 0;
for (int i = pre[u]; i != -1; i = E[i].nxt) {
int v = E[i].v;
if (E[i].c && d[u]+1 == d[v]) {
int tmp = DFS(v, min(flow, E[i].c));
E[i].c -= tmp, E[i^1].c += tmp;
flow -= tmp, ret += tmp;
if (!flow) break;
}
}
if (!ret) d[u] = -1;
return ret;
}
int Dinic() {
int ret = 0;
while (BFS()) ret += DFS(s, INF);
return ret;
}
int main() {
init();
int a, b, h, d; scanf("%d%d%d%d", &a, &b, &h, &d);
for (int i = 1; i <= h+1; i++)
for (int j = 1; j <= a; j++)
for (int k = 1; k <= b; k++)
id[i][j][k] = ++num;
s = 0, t = ++num;
for (int j = 1; j <= a; j++)
for (int k = 1; k <= b; k++)
insert(s, id[1][j][k], INF),
insert(id[h+1][j][k], t, INF);
for (int i = 1; i <= h; i++)
for (int j = 1; j <= a; j++)
for (int k = 1; k <= b; k++) {
int c; scanf("%d", &c);
insert(id[i][j][k], id[i+1][j][k], c);
}
for (int i = d+1; i <= h+1; i++)
for (int j = 1; j <= a; j++)
for (int k = 1; k <= b; k++) {
int x, y;
for (int l = 0; l < 4; l++)
if (id[i][x = j+move[0][l]][y = k+move[1][l]])
insert(id[i][j][k], id[i-d][x][y], INF);
}
printf("%d", Dinic());
return 0;
}