题目链接:http://poj.org/problem?id=3009
题意:
题目很复杂,直接抽象化解释了。给你一个w * h的矩形格子,其中有包含一个数字“2”和一个数字“3”,剩下的格子由“0”和“1”组成,目的是计算从“2”走到“3”的最短步数,“1”代表障碍物,“0”代表可以通行。“2”可以往周围四个方向走,如果往某一个方向走,那么停下来的条件是,当这个方向上存在障碍物“1”,且会停在这个障碍物的前一个格子,并会击碎这个障碍物;如果选择的方向上没有障碍物“1”也没有终点“3”,那么就会一直运动下去,直到出界。如果遇到“3”,那么就算一种到达终点的方法。每选择往一个方向运动,就算一步。如果不能到达或者到达的步数大于10,那么就算失败,输出-1.
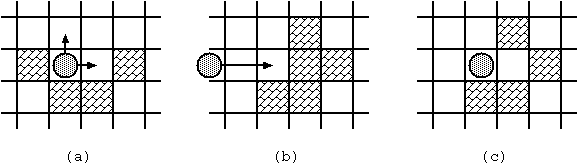
拿题目给的图再说明下吧~
图a:球可以往上和右运动,往上运动直到遇到障碍物才会停下,如果没有障碍物就会出界;往右运动,走一个格子后就会遇到障碍物,此时球停在第二行第三列,且第二行第四列的障碍物被击碎,变为空白格,即“0”。不能往下运动,因为与球相邻的就存在障碍物“1”,球至少运动一个格子才会击碎阻碍它的障碍物。
图b:球如果往右运动的话,会停在第二行第二列的位置,且第二行第三列的障碍物会被击碎变为空白格。
图c:球可以往上,左,右运动,往上和左会出界,往右会停在第二行第三列的位置,且第二行第四列的障碍物会被击碎。
思路:
求最短步数首先想到的是BFS,无奈BFS无法回溯,即无法恢复之前的状态,所以实现起来过于复杂。然后只好利用DFS了,但是DFS要搜索整个解答树才能找到最优解,好在题目给的限制条件是深度不能大于10,也就是O(410),1e6的时间复杂度,可以满足题意了。剩下的就是模拟了,注意判断题条件就好,具体看代码吧~
代码:
1 #include <iostream> 2 #include <cmath> 3 #include <cstdio> 4 #include <cstring> 5 #include <cstdlib> 6 #include <stack> 7 #include <queue> 8 #include <vector> 9 #include <algorithm> 10 #include <string> 11 12 typedef long long LL; 13 using namespace std; 14 const int MAXN = 20; 15 int map[MAXN + 3][MAXN + 3]; 16 int stepX[] = {-1, 1, 0, 0};//四个方向:上、下、左、右 17 int stepY[] = {0, 0, -1, 1}; 18 int ans;//最短步数 19 int w, h;//w 为宽度(y) ,h为高度(x),注意下 20 int stX, stY, edX, edY;//开始时“2”的位置和“3”的位置坐标 21 22 int check(int x, int y) {//返回 非2 代表可以往这个方向走 返回 非1 代表会停下来 23 if(map[x][y] == 0 || map[x][y] == 2 ) return 1; 24 else if(map[x][y] == -1 || map[x][y] == 1) return 2;//出界或者有障碍物 25 else return 3; 26 } 27 28 void backtrack(int x, int y, int t) { 29 if(x == edX && y == edY || t > 10) {//到达终点或者深度大于10 30 ans = (t < ans ? t : ans);//更新最短步数 31 } 32 else { 33 for(int i = 0; i < 4; i++) {//往四个方向试探 34 int tx = x, ty = y; 35 if(check(tx + stepX[i], y + stepY[i]) != 2) { //可以往当前方向运动 36 while(check(tx + stepX[i], ty + stepY[i]) == 1) { //没有障碍物 或 未到达终点的话就一直运动下去 37 tx += stepX[i], ty += stepY[i]; 38 } 39 if(map[tx + stepX[i]][ty + stepY[i]] == 1) {//遇到障碍物停止运动 40 map[tx + stepX[i]][ty + stepY[i]] = 0;//击碎障碍物 41 t++; //步数加1 42 backtrack(tx, ty, t);//继续从障碍物前一个格子开始走 43 --t; //回溯时恢复现场 44 map[tx + stepX[i]][ty + stepY[i]] = 1; 45 } 46 else if(map[tx + stepX[i]][ty + stepY[i]] == 3) {//遇到终点停止运动 47 t++; 48 backtrack(tx + stepX[i], ty + stepY[i], t); 49 --t; 50 } 51 } 52 } 53 } 54 } 55 56 int main() { 57 while(scanf("%d%d", &w, &h), w || h ) { 58 memset(map, -1, sizeof(map)); 59 stX = stY = edX = edY = -1; 60 for(int i = 1; i <= h; i++) { 61 for(int j = 1; j <= w; j++) { 62 scanf("%d", &map[i][j]); 63 if(map[i][j] == 2) stX = i, stY = j; //起点 64 else if(map[i][j] == 3) edX = i, edY = j;//终点 65 } 66 } 67 ans = MAXN; 68 backtrack(stX, stY, 0); 69 printf("%d ", ans > 10 ? -1 : ans); 70 } 71 return 0; 72 }