1.堆排序
要求:对于大顶堆,孩子节点的值小于父节点。
说明:数据会存储在数组中,从数组下标1开始存储根节点,假如i为父节点,则2*i是左孩子,2*i+1是右孩子。
方法:向上调整
步骤:
第一步:建堆,从有孩子节点p开始调整,将p的两个孩子节点较大者与父节点(p)交换,再调整交换过的以子节点为根的树,直到以p为根节点的树满足要求。
第二步:调整堆,因为根节点是最大的,保存后;将最后一个节点与根节点交换,调整树,直到满足要求。调用建堆的方法即可。
#include "iostream" #include "vector" using namespace std; //大顶堆的构造,传入的p是父节点,使得以p为根节点的树,满足大顶堆 void HeapAdjust(vector<int> &vec,int p,int n){ int temp=vec[p]; for (int i = 2 * p; i <= n;i*=2) { if (i < n&&vec[i] < vec[i + 1]) i++;//找到两个孩子结点中最大的 if (temp >= vec[i]) break;//根节点大于子节点,则退出 vec[p] = vec[i]; //将孩子节点放到父节点上 p = i; } vec[p] = temp;//将开始的p节点放到最终位置 } //大顶堆排序,调整堆 void HeapSort(vector<int> &vec){ int n=vec.size()-1; //首先将无序数列转换为大顶堆 for (int i = n / 2; i > 0;i--) //注意由于是完全二叉树,所以我们从一半向前构造,传入父节点 HeapAdjust(vec, i, n); //将最大的元素放入目标位置,然后将剩余元素重新构造大顶堆 for (int i = n; i >1;i--){ swap(vec[1], vec[i]); HeapAdjust(vec, 1, i - 1); } } int main(){ //注意数组中第一个值是不参与排序的,无意义的 vector<int> vec={0,23,4,1,2,5,45,3,345,55}; HeapSort(vec); //1 2 3 4 5 23 45 55 345 for (auto item:vec)cout<<item<<" "; return 0; }
2.快排
快排有两个步骤:
第一步:选取数组的第一个数值为枢轴值,而后将数组调整为左边小于枢轴值,右边大于枢轴值。
第二步:分别对枢轴值左边和右边部分执行上述操作。
具体示例如下:
假如有如下数组
![]()
一趟排序之后
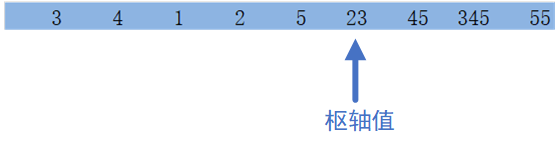
而后分别对枢轴值左边部分和右边部分做同样的操作,最终得到有序数组。
对应的程序代码如下:
#include "iostream" #include "vector" using namespace std; //一趟排序的第一种写法 int ajust_one(vector<int> &vec,int left,int right){ int pivot=vec[left]; //跳出循环是left=right while (left<right){ //如下顺序不可调换 while (left<right&&vec[right]>=pivot)right--; vec[left]=vec[right]; while (left<right&&vec[left]<=pivot)left++; vec[right]=vec[left]; } //将枢轴值放到归位 vec[left]=pivot; return left; } //一趟排序的第二种写法 int ajust_two(vector<int> &vec,int left,int right){ int left_start=left; int pivot=vec[left]; //跳出循环是left=right while (left<right){ //如下顺序不可调换 while (left<right&&vec[right]>=pivot)right--; while (left<right&&vec[left]<=pivot)left++; swap(vec[left],vec[right]);//交换两个值 } //将枢轴值放到归位 vec[left_start]=vec[left]; vec[left]=pivot; return left; } void quickSort(vector<int> &vec,int left,int right){ if(left<right){ int mid=ajust_one(vec,left,right); quickSort(vec,left,mid-1); quickSort(vec,mid+1,right); } } int main(){ vector<int> vec={23,4,1,2,5,45,3,345,55}; quickSort(vec,0,vec.size()-1); //1 2 3 4 5 23 45 55 345 for (auto item:vec)cout<<item<<" "; return 0; }
3.归并排序
经典的分治策略,先分成小问题,而后再合并,最后问题得到求解。
#include "iostream" #include "vector" using namespace std; void ajust(vector<int> &vec,int left,int mid,int right){ vector<int> temp(right-left+1,0); int left_start=left;//保存开始位置 int mid_right=mid+1;// int i=0; while (left<=mid&&mid_right<=right){ if(vec[left]<vec[mid_right]) temp[i++]=vec[left++]; else temp[i++]=vec[mid_right++]; } //将未完成的部分,补到数组后面 while(left<=mid)temp[i++]=vec[left++]; while(mid_right<=right) temp[i++]=vec[mid_right++]; //将临时数组的值拷贝到原数组中 i=0; while(left_start<=right)vec[left_start++]=temp[i++]; } void merge(vector<int> &vec,int left,int right){ if(left<right){ int mid=(left+right)/2; merge(vec,left,mid);//left到mid是有序,包括边界 merge(vec,mid+1,right);//mid+1到right有序,包括边界 ajust(vec,left,mid,right); } } int main(){ vector<int> vec={23,4,1,2,5,45,3,345,55}; merge(vec,0,vec.size()-1); //1 2 3 4 5 23 45 55 345 for (auto item:vec)cout<<item<<" "; return 0; }