中国剩余定理

写在前面：

　　记录了个人的学习过程，同时方便复习

注意

中国剩余定理要求模数全部两两互质，是模数为任意整数的一个特殊条件

中国剩余定理仅仅是解决这一特殊条件下的线性同余方程组的一个巧妙方法

开心一下就好了，它一点也不正规

 

目录

• 内容

• 证明及实现

• 拓展

1. 解的一定存在性

2. 中国剩余定理的局限性

3. 拓展中国剩余定理

 

 

内容

　　孙子定理是中国古代求解一次同余式组的方法。是数论中一个重要定理。又称中国余数定理。

　　一元线性同余方程组问题最早可见于中国南北朝时期（公元5世纪）的数学著作《孙子算经》卷下第二十六题，叫做“物不知数”问题，原文如下：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

　　即，一个整数除以三余二，除以五余三，除以七余二，求这个整数。

　　《孙子算经》中首次提到了同余方程组问题，以及以上具体问题的解法，因此在中文数学文献中也会将中国剩余定理称为孙子定理。

——bia度百科

　　中国剩余定理求解线性同余方程组是一个有意思的算法，它严格要求模数两两互质

　　然而在实际应用中则缺陷很大，我们使用正规的[◹]线性同余方程组解法

　　中国剩余定理仅仅用来活跃一下思维

 

证明及实现

【物不知数】是中国古代著名算题，原载《孙子算经》卷下第二十六题：

今有物不知其数，三三数之剩二；五五数之剩三；七七数之剩二。问物几何?

　　当时虽已有了答案23，但它的系统解法是秦九韶在《数书九章·大衍求一术》中给出的

　　中国剩余定理是中国古算中最有独创性的成就之一，属现代数论中的一次同余式组问题

——bia度百科

　　那么就是求解以下同余方程：　　有x个物件，三个三个数剩2个，五个五个位数剩3个，七个七个数剩2个

　　　　x ≡ 2 (MOD 3)

　　　　x ≡ 3 (MOD 5)

　　　　x ≡ 2 (MOD 7)

　　可以用分治的思想来做

　　先求得这样的三个数，使得对于每个模数而言，仅有模它得到的余数为1

(注意，这样的解法仅在模数两两互质的情况下成立)

　　　　x₁ ≡ 1 (MOD 3)　　x₂ ≡ 0 (MOD 3)　　x₃ ≡ 0 (MOD 3)

　　　　x₁ ≡ 0 (MOD 5)　　x₂ ≡ 1 (MOD 5)　　x₃ ≡ 0 (MOD 5)

　　　　x₁ ≡ 0 (MOD 7)　　x₂ ≡ 0 (MOD 7)　　x₃ ≡ 1 (MOD 7)

　　　　就第一组x₁的同余方程来说，它的解是5*7*n₁

　　　　n₁*35 ≡ 1 (MOD 3)

　　　　也就是 n₁*2 ≡ 1 (MOD 3)

　　　　n₁ == 2，x₁ == 70

　　　　同理得到n₂ == 1，x₂ == 21，n₃ == 1，x₃ == 15

　　因为要求的余数为2，3，2，分别将x₁，x₂，x₃乘上对应的余数

　　再把得到的x₁*2，x₂*3，x₃*2加起来就好了，这样的得到的就是一种解

　　希望求最小正整数解，把得到的数模上3，5，7的最小公倍数就好了

 

　　推广到其他的情形，需要解这样的一组同余方程

　　　　x ≡ k₁ (MOD p₁)

　　　　x ≡ k₂ (MOD p₂)

　　　　......

　　　　x ≡ k_n (MOD p_n)

　　　　(其中p₁，p₂，......，p_n之间两两互质)

　　求出它们的最小公倍数M == ∏ⁿ_i=1 ​p_i (因为这些数两两互质)

　　则对于每一个数p，p与M/p的最大公因数为1

　　使用拓展欧几里得算法求出一组x，y，使得M/p*x + p*y ≡ 1 (MOD M)

　　留下来x就好，y不用管了

　　见[◹]拓展欧几里得算法的应用②

x == (x₁*p₁*k₁ + x₂*p₂*k₂ + ...... + x_n*p_n*k_n) MOD M

　　这样就算好啦

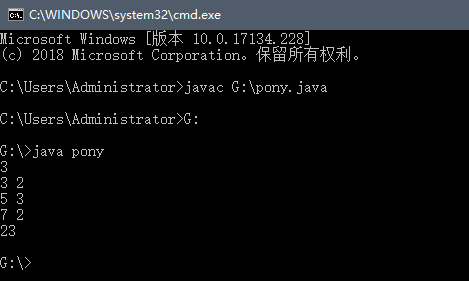
　　代码如下：

C++：

#include<bits/stdc++.h>

using namespace std;

int const MAXN=10010;
int x,y;
int k;//k组同余方程
int a[MAXN];//每个同余方程的余数
int b[MAXN];//每个同余方程的模数
int ans;
int lcm=1;

void exgcd(int a,int b)
{
    if(b==0){x=1;y=0;}
    else{
        exgcd(b,a%b);
        int tmp=x;
        x=y;y=tmp-a/b*y;
    }
    return;
}

int main(int argc,char *argv[],char *enc[])
{
    scanf("%d",&k);
    for(int i=1;i<=k;++i)
        scanf("%d%d",&b[i],&a[i]);
        
    for(int i=1;i<=k;++i)
        lcm*=b[i];
    for(int i=1;i<=k;++i)
    {
        exgcd(lcm/b[i],b[i]);
        x=(x%b[i]+b[i])%b[i];
        
        ans=(ans+(lcm/b[i])*x*a[i])%lcm;
    }
    
    printf("%d",ans);
    return 0;
}

Java：

import java.io.*;
import java.util.*;

class pony{

    static int MAXN=10010;
    static int x,y;
    static int k;//k组同余方程
    static int[] a=new int[MAXN];//每个同余方程的余数
    static int[] b=new int[MAXN];//每个同余方程的模数
    static int ans;
    static int lcm=1;

    static void exgcd(int a,int b)
    {
        if(b==0){x=1;y=0;}
        else{
            exgcd(b,a%b);
            int tmp=x;
            x=y;y=tmp-a/b*y;
        }
        return;
    }

    public static void main(String[] args) throws Exception {
        
        Scanner cin=new Scanner(System.in);
        
        k=cin.nextInt();
        for(int i=1;i<=k;++i)
        {
            b[i]=cin.nextInt();
            a[i]=cin.nextInt();
        }

        for(int i=1;i<=k;++i)
            lcm*=b[i];
        for(int i=1;i<=k;++i)
        {
            exgcd(lcm/b[i],b[i]);
            x=(x%b[i]+b[i])%b[i];

            ans=(ans+(lcm/b[i])*x*a[i])%lcm;
        }

        System.out.println(ans);
    }
}

因为两两互质，最小公倍数就是这些数的积，我在对唯一分解定理的研究中提到过

 

拓展

• 解的一定存在性

　　证明：

　　　　同余方程x*a ≡ b (mod c)的成立条件是：gcd(x*a，c)为b的因子，也就是gcd(a，c)为b的因子，详细证明见[◹]拓展欧几里得算法的应用④

　　　　因为每组同余方程里面，c都为素数，只要a不是c的倍数，那么gcd(a，c)都是1，1一定是b的因子

　　　　所以只要模数全部为素数，且a不是模数的倍数，对于每一个同余方程，解x一定存在

　　　　而对于所有的同余方程，因为模数两两互素，不存在同余方程组之间的冲突，所以一定有解

　　同余方程组的解的存在条件，见[◹]线性同余方程组

• 中国剩余定理的局限性

　　中国剩余定理仅仅适用于每个模数两两互质的情况

　　但是最常见的情况还是所有模数不满足两两互质

　　这样的话，中国剩余定理就不再适用

 

　　中国剩余定理的思路是整体处理

　　但是当模数不满足两两互素时，就不能处理其中关键的一步：

　　不满足两两互素，即某些模数之间的最大公因数不是1，解出的方程余数不为1

 　　而这只是在模数不满足两两互质的情况下，不能使用中国剩余定理得到解而已，不一定没有解

 

• 解线性同余方程组(拓展中国剩余定理)

　　中国剩余定理仅仅适用于每个模数两两互质的情况，仅仅是一种在特殊情况下的巧妙解法

　　但是最常见的情况还是所有模数不满足两两互质

　　这样的话，中国剩余定理就不再适用

　　需要使用正规的[◹]线性同余方程组解法