Airthmetic_stackAndQueue'

S

tack and Queue

1. First. Reverse a stack without any data structure -- 逆序一个栈，不能用任何一个数据结构

Thinking ： 对于栈来说，基本的特征就是先进后出，基本的操作就是pop，push，peek这三种，如果要想达到逆序一个栈，也就是是将12 3的栈顺序变成3 2 1的顺序

 

当然正常的思维就是要是能够再申请一个栈就可以重新导入另外一个栈实现逆序，但是条件就是不能再次申请任何一个数据结构，所以能在这个栈上做做文章，再想能不能用交换的思想，把栈顶和栈底的交换，然后第二个和倒数第二个交换，但是要想到在栈中的基本操作是不可能实现的，所以想到函数，（好嘛，必须承认想到函数，利用函数栈思想也不是那么容易想到的），函数在实际操作的过程中其实就是一个栈的形式在内存中，当！是不是就可以利用好这个栈来实现这里定义的栈的逆序

好，现在就是集中解决一个问题-- 如何好好利用函数栈来逆序我们定义的栈？

嗯，其实想到这里也只是打开了新世界大门，还没有真正踏进去，所以以下会有关计算机基础的知识的内容为入门条件，当然我会尽可能的描述清楚一点

首先对函数栈帧的知识扫个盲，在执行到函数代码的时候，操作系统是会给一个函数分配栈帧的，这是为了简化内存的管理，使程序内存空间划分为栈和堆，在堆中是可以随机分配的，而在栈中是必须连续分配的内存的，这也是能够实现这里解法的关键，一个函数调用另外一个函数，不管这个被调用函数多大，都是紧接着调用函数的栈帧的，因为如果考虑的多并发的问题的话，操作系统不这样实现就会出现问题。所以下面是操作系统中真实的多线程情况下的内存中程序堆栈分布图：

好，现在扫盲完成之后就真正进入解题部分，后面对栈帧的细节方面我就不一一细说了，详细的分配方式可以参照jvm，我主要讲如何利用这个函数栈帧来解决定义我们写的栈帧逆序的问题。

函数栈帧里面的值是可以记录下的我们定义的数据结构的，但是我们还是不能直接操作函数栈的，这是操作系统的权限，并且函数栈return完就自动消失，但是我们可以巧妙地利用函数栈的空间，那就是利用递归，递归这种东西就是对函数栈帧深度理利用最好的例子。

所以我们现在的思路就进行到了使用递归的方法，间接利用函数帧，对程序中申请的栈中元素进行逆序，现在开始真正的算法之门，

单纯只对栈进行操作的话，并且用递归的方法，如下图所示

 

所以想要做到上面的这种反转的操作，第一步就必须要先得到栈的bottom数据，并且还要删除它，还要保留这个bottom值在本栈帧现场，对于得到bottom数据并且删除且返回bottom值，针对栈结构的相关操作来说，还是利用递归可以实现, 图示如下

 

public int getAndRemoveBottom(Stack<Integer> s){

// first get the top value

int temp_res = s.pop();

// second judge the stack is empty

if(s.isEmpty()){ // if empty--this pop value is bottom value

return temp_res;

}

 

// third keep going pop -- use the function stack to keep going find the bottom and record the every pop value

int bottom = getAndRemoveBottom(s);

// fourth push the pop value -- not the bottom value

s.push(temp_res);

// fifth keep returning the bottom value -- until the reach the top

return bottom;

}

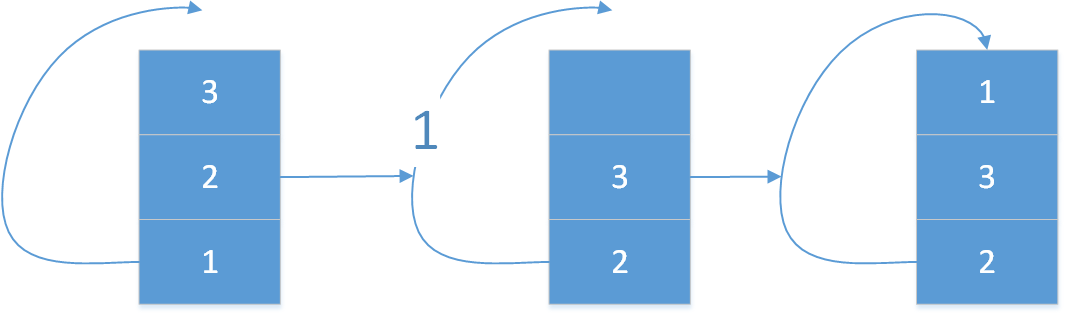
可以看到上面所解决的只是一次的画面帧，现在就是要连续起来所有的类似的这样的画面帧，直到整个栈结构被逆序完成，就是仅仅做到的这一步：

 

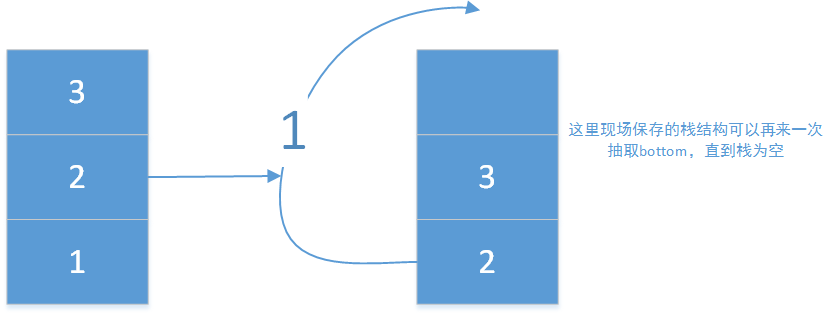
要让整个画面帧都动起来，所以还需要一个递归函数：

public void reverse(Stack<Integer> s){

// rubust check and eage test

if(s.isEmty()){

System.out.println("there is no data here");

return;

}

 

// here we get bottom of a frame

int bottom = getAndRemoveBottom(s);

// here we need to get more bottom of a frame until stack is empty

reverse(s);

// here we need to push every frame's bottom

s.push(bottom);

return;

}

---

写到这里基本上就大功告成了，还是贴一下整体代码

public class ReverseStack {

 

public int getAndRemoveBottom(Stack<Integer> s){

int temp = s.pop();

if(s.isEmpty()){

return temp;

}

 

int bottom = getAndRemoveBottom(s);

s.push(temp);

return bottom;

}

 

public void reverse(Stack<Integer> s){

if(s.isEmpty()){

System.out.println("there is no data!");

return;

}

 

int bottom = getAndRemoveBottom(s);

reverse(s);

s.push(bottom);

}

 

public static void main(String[] args) {

ReverseStack sta = new ReverseStack();

 

Stack<Integer> data_stack = new Stack<Integer>();

 

data_stack.push(1);

data_stack.push(2);

data_stack.push(3);

 

sta.reverse(data_stack);

 

System.out.println(data_stack.toString());

}

}

最后我再来解释一下为什么最开始要提出函数栈的思路，因为要我去单想逆序一个数据结构，不需要任何其他的数据结构做辅助，我是想不出来递归的，而且跟别说上面用到的两层递归的思路，感觉看起来很抽象，但是这些思路放在函数栈帧里面去看变量的变化，就不会那么的抽象，也能更深层次的理解为什么递归是可以实现这个栈结构的逆序，在没有任何其他空间辅助的情况下。主要就是函数的栈可以帮你去保存你需要的一步步保存的数据和变化的数据结构，就可以在此思路上大做文章。

下面一些符号的解释 ：ebp 开启一个函数栈帧的栈底，push ebp

eip call指令的下一条指令的地址 ； esp 开启函数栈帧的栈顶地址

 

所以从上面的栈帧变化中可以看出原理 -- 其实就是在reverse的栈帧中保存一个当时栈帧中stack里面bottom值，并且同时改变stack的值，然后等到return的时候就可以每次push bottom值啦，就成功了