提出问题
最长回文子串问题:给定一个字符串,求它的最长回文子串长度。
如果一个字符串正着读和反着读是一样的,那它就是回文串。如a、aa、aba、abba等。
暴力解法
简单粗暴:找到字符串的所有子串,遍历每一个子串以验证它们是否为回文串。一个子串由子串的起点和终点确定,对于一个长度为n的字符串,共有n^2个子串。这些子串的平均长度大约是n/2,因此这个解法的时间复杂度是 (O(n^3))。明显不可取。
方法改进
回文子串是连续的,而且是对称的。长度为奇数回文串以最中间字符的位置为对称轴左右对称,而长度为偶数的回文串的对称轴在中间两个字符之间的空隙。可否利用这种对称性来提高算法效率呢?答案是肯定的。我们知道整个字符串中的所有字符,以及字符间的空隙,都可能是某个回文子串的对称轴位置。可以遍历这些位置,在每个位置上同时向左和向右扩展,直到左右两边的字符不同,或者达到边界。对于一个长度为n的字符串,这样的位置一共有 n+n-1=2n-1 个,在每个位置上平均大约要进行 n/4 次字符比较,于是此算法的时间复杂度是 (O(n^2))。
另外一种改进方法是利用动态规划,DP[i][j]定义成子串[i, j]是否是回文串。外循环 i从 n−1 往 0 遍历,内循环 j 从 i 往 n−1 遍历,若s[i]==s[j]:
- 若i==j,则dp[i][j]=true;
- 若i和j是相邻的,则dp[i][j]=true;
- 若i和j中间只有一个字符,则dp[i][j]=true;
- 否则,检查dp[i+1][j-1]是否为true,若为true,那么dp[i][j]就是true。
前三条可以合并,即 j−i≤2。求得dp[i][j]真值后,也可快速解决问题。时间复杂度:(O(n^2))。
Manacher's Algorithm
对于 (O(n^2)) 的复杂度,或许还不满足,是否可以再优化一些呢?
先分析改进方法中的缺陷,利用回文中心需要分奇偶两种情况讨论,两种改进都会重复访问子串,降低效率。
Manacher's Algorithm正是针对这两个问题进行进一步的改进,将时间复杂度降到了神奇的 (O(n)):
问题一:回文长度奇偶性问题
为了不区分奇偶两种情况,对字符串作预处理,在所有字符之间(包括首尾)插入相同字符如'#',处理之后所有的子串都是奇数长度的。如aba→#a#b#a#。
插入的是同样的符号,且符号不存在于原串,因此子串的回文性不受影响,原来是回文的串,插完之后还是回文的,原来不是回文的,依然不会是回文。
问题二:重复访问问题
定义回文半径:回文串中最左或最右位置的字符与其对称轴的距离。算法中定义回文半径数组 (RL),(RL[i]) 表示以第i个字符为对称轴的回文串的回文半径。
定义 (MaxRight),表示当前访问到的所有回文子串,所能触及的最右一个字符的位置。另外还要记录下 (MaxRight) 对应的回文串的对称轴所在的位置,记为 (pos)。
核心代码:RL[i] = i < MaxRight ? min(RL[2*pos-i], MaxRight-i) : 1;
理解了这行代码,可以说就理解了这个算法。我们来分情况讨论:
(1)i < MaxRight时,可以再分两种情况:
①MaxRight - i > RL[2*pos-i],如下图,以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中,由于 i 和 j 对称,以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中,所以必有 P[i] = P[j]。
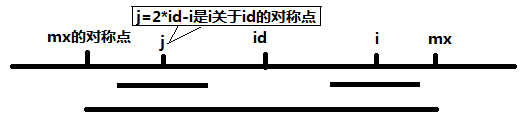
②MaxRight - i < RL[2*pos-i],如下图,以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中,但是基于对称性可知,下图中两个绿框所包围的部分是相同的,也就是说以S[i]为中心的回文子串,其向右至少会扩张到mx的位置,也就是说 P[i] >= mx - i。
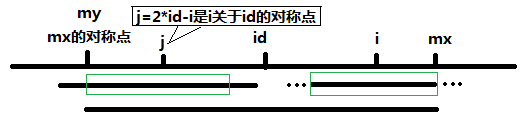
(2)i > MaxRight时,无法对 P[i]做更多的假设,只能P[i] = 1,然后再去慢慢匹配了。
代码实现
返回最长的回文子串。代码中resLen为处理后字符串的最大回文半径,对应到原来的字符串中时,只需-1即是整个回文串的长度。
string Manacher(string s) {
//预处理
string t = "#";
for (int i = 0; i < s.size(); ++i) {
t += s[i];
t += "#";
}
vector<int> RL(t.size(), 0);
int MaxRight = 0, pos = 0;
int resLen = 0, resCenter = 0;
for (int i = 0; i < t.size(); ++i) {
RL[i] = MaxRight > i ? min(RL[2 * pos - i], MaxRight - i) : 1;
while (i-RL[i] >=0 && i+RL[i] < t.size() && t[i + RL[i]] == t[i - RL[i]])//扩展,注意边界
++RL[i];
//更新最右端及其中心
if (MaxRight < i + RL[i] -1) {
MaxRight = i + RL[i] -1;
pos = i;
}
if (resLen < RL[i]) {
resLen = RL[i];
resCenter = i;
}
}
return s.substr((resCenter - resLen + 1) / 2 , resLen - 1);
}
时间复杂度:(O(n))。在参考链接中有比较详细的证明过程。