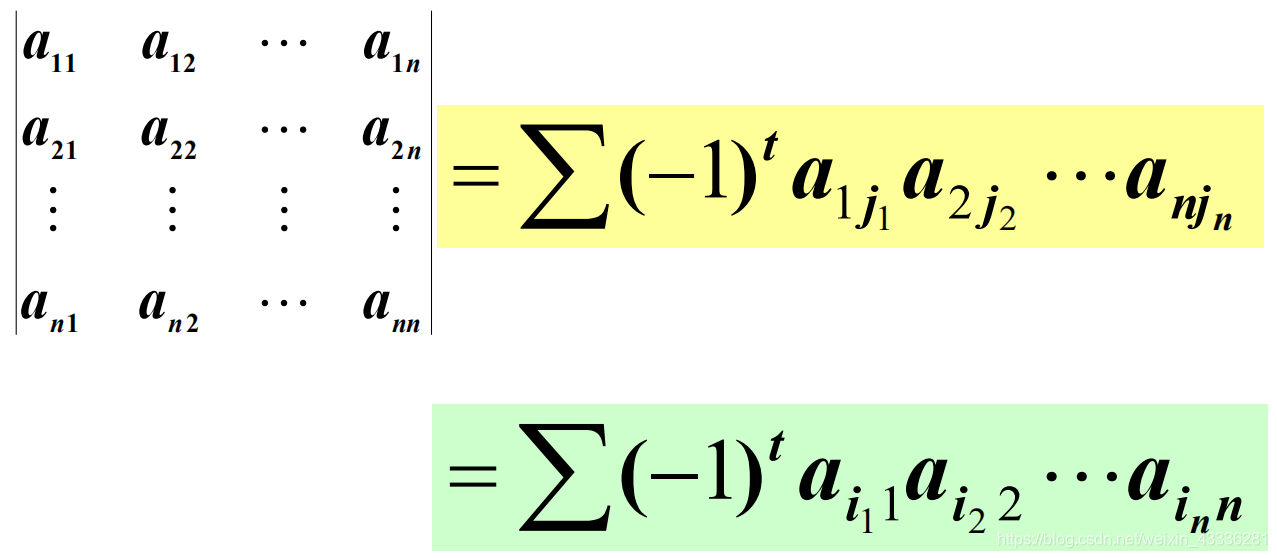线性代数——第一章：行列式——§1.1 行列式的定义

§1.1 行列式的定义

一、二阶和三阶行列式

二元线性方程组

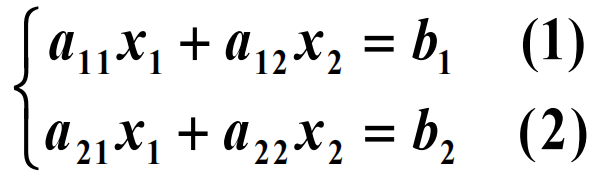
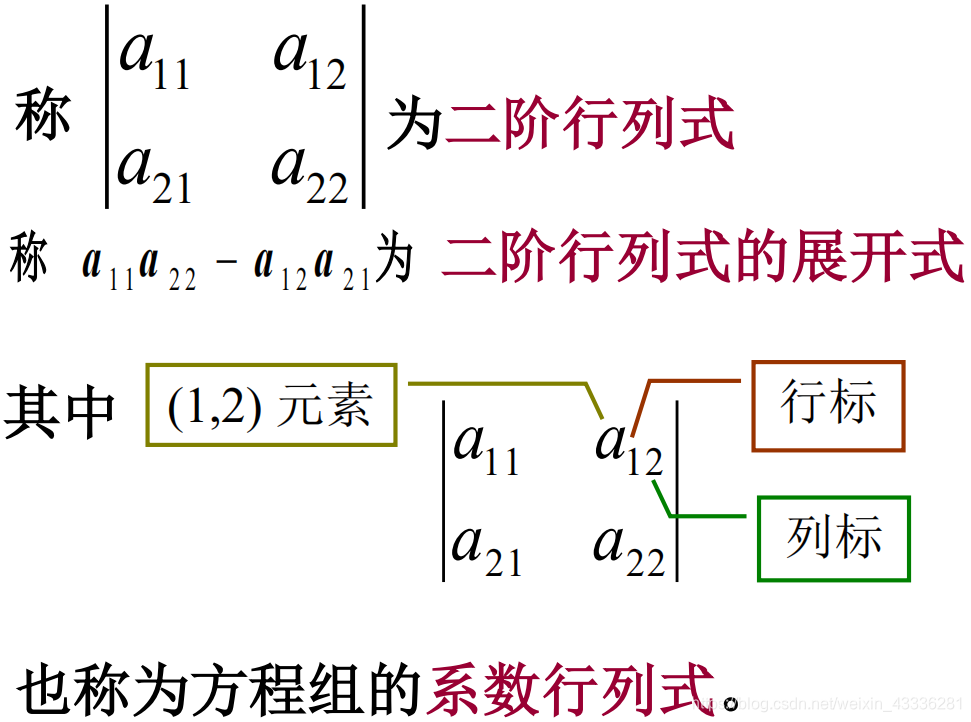
对角线法则

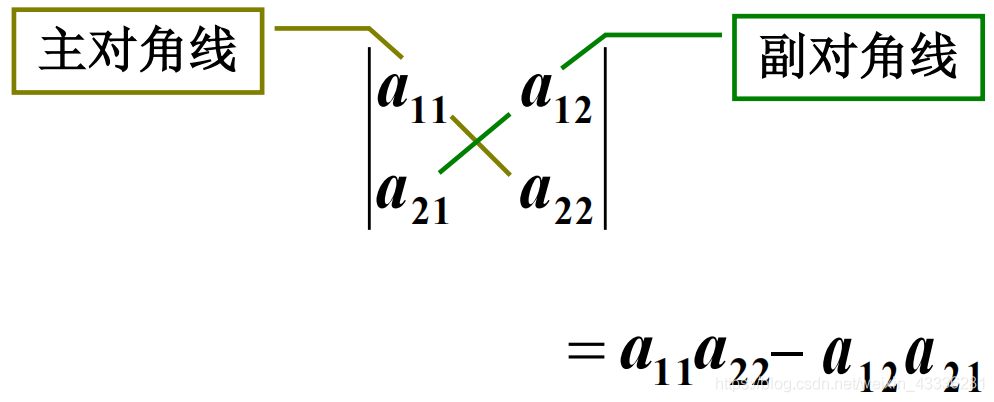
三元线性方程组

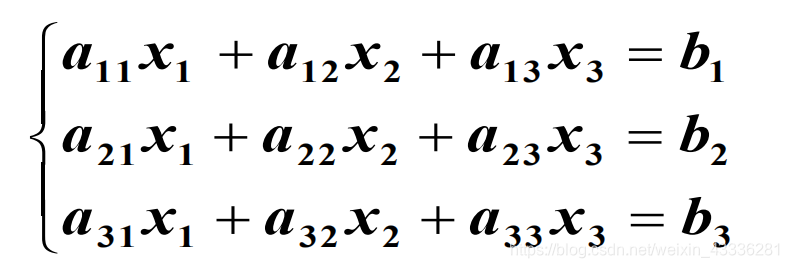
对角线法则

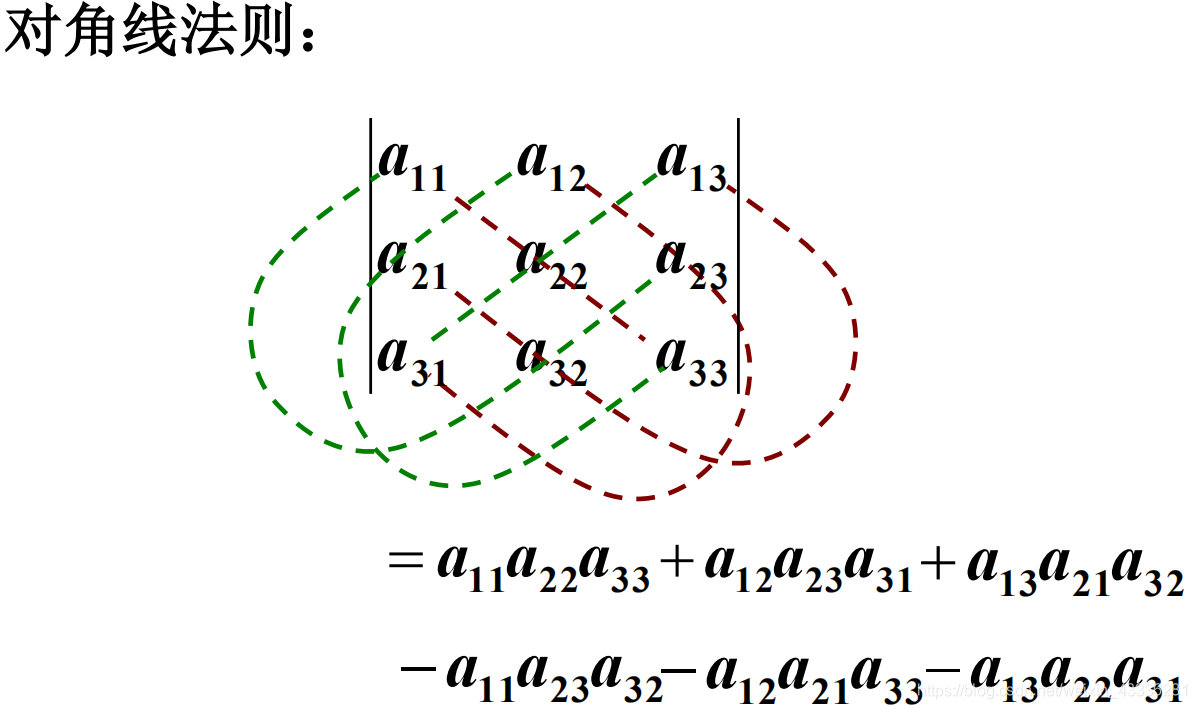
二、逆序数和对换

定义1：把 n 个不同的元素排成的一列, 称 为这 n 个元素的一个全排列, 简称排列。

把 n 个不同的元素排成一列, 共有 Pn个排列。一般地，Pn= n·(n-1)·…·3·2·1= n!

标准排列：标号由小到大的排列。

定义2：在 n个 元素的一个排列中，若某两个元素排列的次序与标准次序不同，就称这两个数构成一个逆序，一个排列中所有逆序的总和称为这个排列的逆序数。

一个排列的逆序数的计算方法：设 p₁ p₂ … p_n 是 1，2，…，n 的一个排列，用 t_i 表示元素 p_i 的逆序数，即排在 p_i 前面并比p_i 大的元素有 t_i 个，则排列的逆序数为：t = t₁ + t₂ + … + t_n。

逆序数为奇数的排列称为奇排列。
逆序数为偶数的排列称为偶排列。

三、n阶行列式的定义

观察二、三阶行列式，得出下面结论：

1. 每项都是处于不同行不同列的n个元素的乘积。
2. n 阶行列式是 n！项的代数和。
3. 每项的符号都是由该项元素下标排列的奇偶性所确定。

重要结论

(1.1) 对角行列式

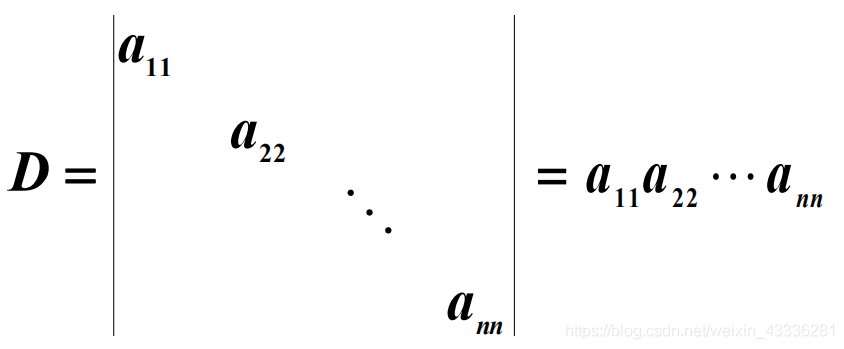
(1.2) 副对角行列式

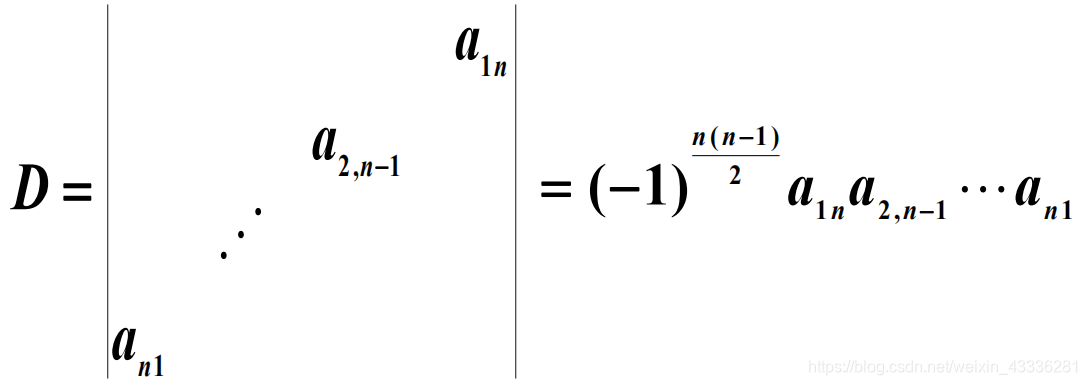
(2.1)下三角形行列式

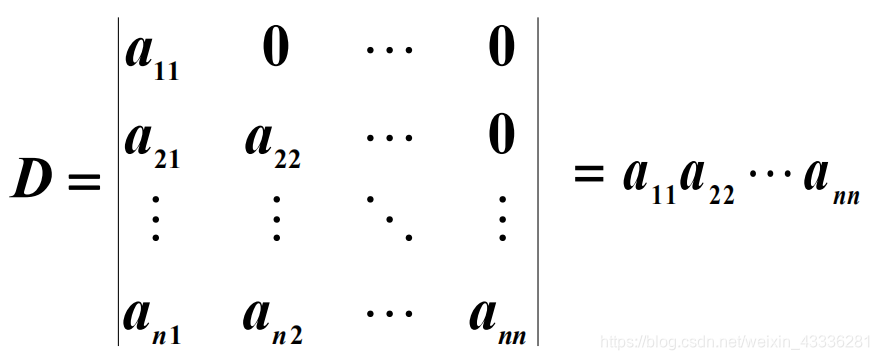
(2.2)上三角形行列式

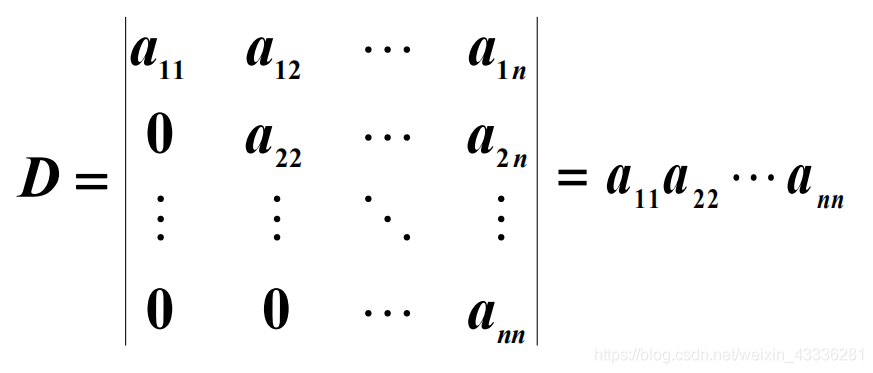
(2.3）

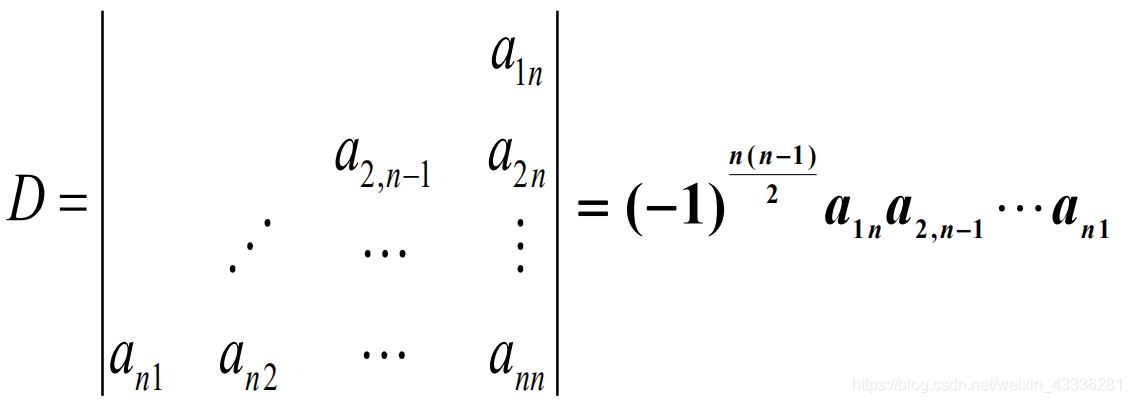
(2.4）

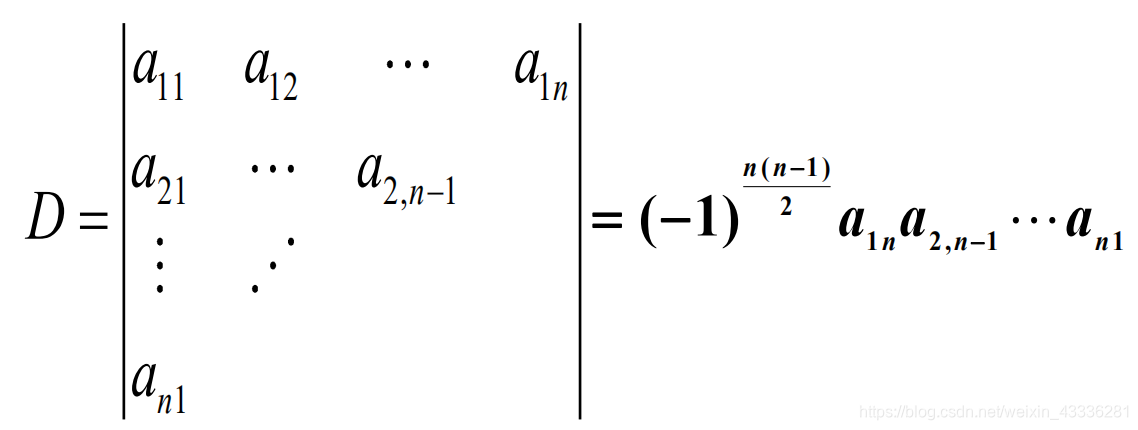
行列式的等价定义