贪吃的九头龙

【题目描述】

有一天，有M个脑袋的九头龙看到一棵长有N个果子的果树，想把果子一口全部吃掉。可是必须照顾到每个头，因此它需要把N个果子分成M组，每组至少有一个果子，让每个头吃一组。

这M个脑袋中有一个最大，称为“大头”，是众头之首，它要吃掉恰好K个果子，而且K个果子中理所当然地应该包括唯一的一个最大的果子。果子由N-1根树枝连接起来，由于果树是一个整体，因此可以从任意一个果子出发沿着树枝“走到”任何一个其他的果子。

对于每段树枝，如果它所连接的两个果子需要由不同的头来吃掉，那么两个头会共同把树枝弄断从而把果子分开；如果这两个果子是由同一个头来吃掉，那么这个头会直接把果子连同树枝一起吃掉。每段树枝都有一个吃下去的“难受值”，而九头龙的难受值就是所有头吃掉的树枝的“难受值”之和。

九头龙希望你可以算出最小的“难受值”。

【输入描述】

输入的第1行包含三个整数N(1 <= N <= 300)、M(2 <= M <= N)、K(1 <= K <=N)。N个果子依次编号1、2、······、N，且最大的果子的编号总是1。第2行到第N行描述了果树的形态，每行包含三个整数A(1 <= A <= N)、B(1 <= B <= N)、C(0 <= C <= 10^5)，表示存在一段难受值为C的树枝连接果子A和果子B。

【输出描述】

输出仅有一行，包含一个整数，表示在满足“大头”的要求的前提下，九头龙的难受值的最小值。如果无法满足要求，输出-1。

【样例输入】

8 2 4

1 2 20

1 3 4

1 4 13

2 5 10

2 6 12

3 7 15

3 8 5

【样例输出】

4

【数据范围及提示】

例如图1所示的例子中，果树包含8个果子，7段树枝，各段树枝的“难受值”标记在了树枝的旁边。九头龙有两个脑袋，大头需要吃掉4个果子，其中必须包含最大的果子。即N=8，M=2，K=4：

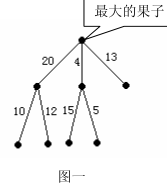
图一描述了果树的形态，图二描述了最优策略。

源代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int N,M,K,num,f[301][301][2],Tmp[301][2],Next[301<<1],Data[301<<1],Value[301<<1],h[301]={0},Sum[301]={0};
void Add(int t1,int t2,int t)
{
    Next[++num]=h[t1];
    h[t1]=num;
    Data[num]=t2;
    Value[num]=t;
}
void Min(int &t1,int t2,int t3)
{
    t1=min(min(t1,t2),t3);
}
void DP(int X,int From)
{
    int Y,t;
    f[X][1][1]=0;
    f[X][0][0]=0;
    Sum[X]=1;
    for (int a=h[X];a;a=Next[a])
      if ((Y=Data[a])!=From)
      {
        DP(Y,X);
        Sum[X]+=Sum[Y];
        if (M==2)
          t=Value[a];
        else
          t=0;
        memcpy(Tmp,f[X],sizeof(f[X]));
        memset(f[X],0x3f,sizeof(f[X]));
        for (int b=Sum[X];b>=0;b--)
        {
            if (b>0)
              for (int c=b-1;c>=0;c--)
                Min(f[X][b][1],Tmp[b-c][1]+f[Y][c][0],Tmp[b-c][1]+f[Y][c][1]+Value[a]);
            for (int c=b;c>=0;c--)
              Min(f[X][b][0],Tmp[b-c][0]+f[Y][c][0]+t,Tmp[b-c][0]+f[Y][c][1]);
        }
      }
}
int main()
{
    memset(f,0x3f,sizeof(f));
    scanf("%d%d%d",&N,&M,&K);
    if (N-K<M-1)
    {
        printf("-1
");
        return 0;
    }
    num=1;
    for (int a=1;a<N;a++)
    {
        int t,t1,t2;
        scanf("%d%d%d",&t1,&t2,&t);
        Add(t1,t2,t);
        Add(t2,t1,t);
    }
    DP(1,0);
    printf("%d
",f[1][K][1]);
    return 0;
}