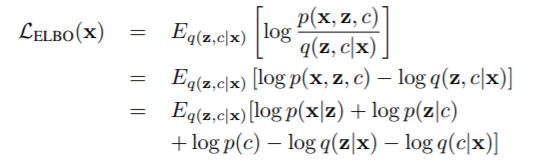1.高斯混合分布GMM
https://zhuanlan.zhihu.com/p/30483076
https://blog.csdn.net/jinping_shi/article/details/59613054
https://zhuanlan.zhihu.com/p/60649774
高斯混合模型(Gaussian Mixture Model)是机器学习中一种常用的聚类算法。它是多个高斯分布的线性组和:
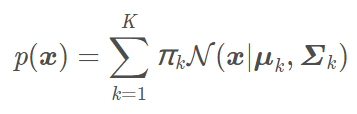
每个分模型都有自己的均值和方差。Πk是混合稀疏,和为1。
那么当给定一个样本,怎么确定它对应的Πk的系数呢?
这就用到了EM算法,能够针对数据集计算出Πk参数。使得这个混合分布更能代表原始数据的真实分布。“多个高斯分布的线性叠加能拟合非常复杂的密度函数;通过足够多的高斯分布叠加,并调节它们的均值,协方差矩阵,以及线性组合的系数,可以精确地逼近任意连续密度。”
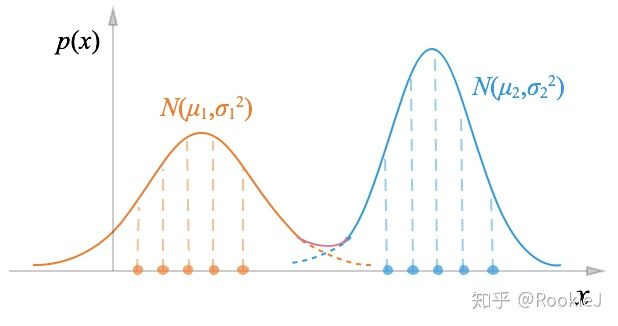
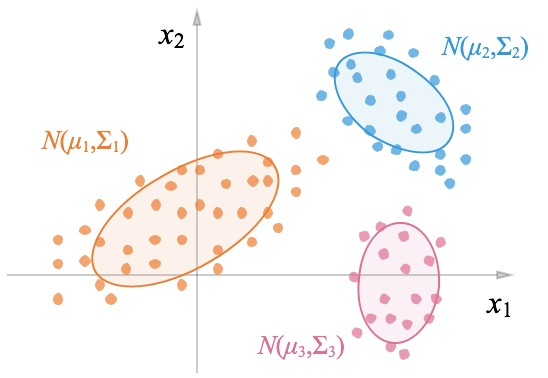
上图是两个一维的高斯混合,下面也可以看出来,整个的数据分布由三个不同的高斯分布组成:
2.GaussianMixture应用
https://scikit-learn.org/stable/modules/generated/sklearn.mixture.GaussianMixture.html
https://www.cnblogs.com/dahu-daqing/p/9456137.html
初始化模型中的GMM参数:
from sklearn.mixture import GaussianMixture
fit函数:使用EM算法估计模型参数,predict计算出每个样本属于每个子高斯模型的概率:

比如上面的结果分数,是针对三个样本和四个子高斯模型,根据得分最高的来,那么类别分别是2 3 3。
2.1 形参
class sklearn.mixture.GaussianMixture(n_components=1, *, covariance_type='full', tol=0.001, reg_covar=1e-06, max_iter=100,
n_init=1, init_params='kmeans', weights_init=None, means_init=None, precisions_init=None, random_state=None,
warm_start=False, verbose=0, verbose_interval=10)
n_components:混合物成分的数量。
covariance_type : {“完整”(默认),“并列”,“诊断”,“球形”}
描述要使用的协方差参数类型的字符串。必须是以下之一:
- ‘充分’ full:每个分量都有自己的通用协方差矩阵
- ‘绑’ tied:所有分量共享相同的通用协方差矩阵
- ‘diag’ : 每个分量都有自己的对角协方差矩阵
- ‘球形’: 每个组件都有其自己的单个方差
2.2 属性
https://blog.csdn.net/qq_43744752/article/details/104775623
![]()
- weights_ :每种混合物成分的重量。
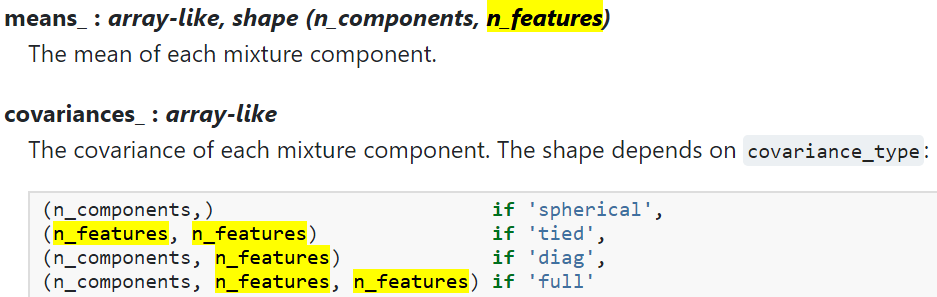
- means_ :每个混合物成分的平均值。(需要了解多维高斯分布)
- covariances_ :每个混合物成分的协方差。
2.3 例子
例子:
import torch
from sklearn.mixture import GaussianMixture
a=torch.randn(100,3)
gmm = GaussianMixture(n_components=3, covariance_type='diag')
gmm.fit(a)
print(gmm.means_)
print(gmm.covariances_)
#输出:
[[ 0.13355099 -0.87731539 0.11807917]
[-0.02544988 0.36799893 0.93609104]
[-0.1310032 0.52882658 -0.38371371]]
[[0.96960938 0.4109546 0.70868165]
[0.74410499 0.72071033 0.31313133]
[1.2172497 0.43499053 0.39583606]]
3.GMM损失计算
![]()