bzoj2728 [HNOI2012]与非

题目链接：http://www.lydsy.com/JudgeOnline/problem.php?id=2728

Description

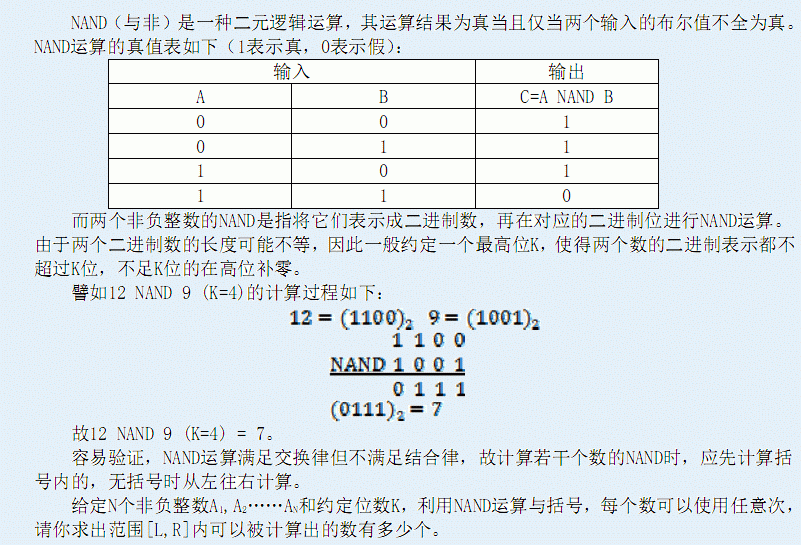
Input

输入文件第一行是用空格隔开的四个正整数N，K，L和R，接下来的一行是N个非负整数A1,A2……AN，其含义如上所述。 100%的数据满足K≤60且N≤1000,0<=Ai<=2^k-1,0<=L<=R<=10^18

Output

仅包含一个整数，表示[L,R]内可以被计算出的数的个数

Sample Input

3 3 1 4
3 4 5

Sample Output

HINT

样例1中，(3 NAND 4) NADN (3 NAND 5) = 1，5 NAND 5 = 2，3和4直接可得。

Source

day1

题解

一道神题啊。。

看了下网上的题解。。

发现全都看不懂啊啊啊啊啊啊

所以我就说一下并查集的做法。。

众所周知，如果对于第i位和第j位，如果A中的所有数的这两位都相等。。辣么。。他们组合出来的书的这两位也相等。。

好像是废话。。

然后就可以用并查集将i和j并起来。。

接下来就是类似于数位Dp的东西。。

比如说。。

将目标x拆成二进制。。

如果当前一位是1，那么。。如果当前一位组合出来是0，代表接下来的每个并查集块既可以选1也可以选0。

以此类推。。

不懂就看到代码吧。。

solve里面的break就代表如果当前位已经确定了。。后面继续做可能会超出范围。。所以break了。。

什么我讲的不清楚？。。

没办法我语文太差了。。

 1 #include <cstdio>
 2 #include <cstring>
 3 #define K 65
 4 #define N 1500
 5 using namespace std;
 6 typedef long long ll;
 7 namespace acheing{
 8     int i,j,k,n,m,x,y,t,f[K],b[K],tot,res;
 9     ll l,r,a[N];
10     int find(int x){return f[x]==x?x:f[x]=find(f[x]);}
11     ll solve(ll x){
12         memset(b,-1,sizeof b);ll ans=0,res=tot;
13         if (x+1>=(1ll<<m))return 1ll<<res;x++;
14         for (i=m-1;i>=0;i--){
15             if ((x>>i)&1){t=find(i);if (b[t]==1)continue;if (b[t]==-1){res--;b[t]=1;}ans+=(1ll<<res);if (!b[t])break;}
16             else{t=find(i);if (b[t]==-1)b[t]=0,res--;if (b[t])break;}
17         }
18         return ans;
19     }
20     bool check(int x,int y){
21         for (int i=1;i<=n;i++){
22             if ((((a[i]>>x)^(a[i]>>y))&1))return 0;
23         }
24         return 1;
25     }
26     void init(){
27         for (i=0;i<m;i++)f[i]=i;
28         for (i=0;i<m;i++)for (j=0;j<i;j++)if (check(i,j)){f[find(i)]=find(j);break;}
29         for (i=0;i<m;i++)if (i==find(i))tot++;
30     }
31     void main(){
32         scanf("%d%d%lld%lld",&n,&m,&l,&r);
33         for (i=1;i<=n;i++)scanf("%lld",&a[i]);
34         init();
35         printf("%lld
",solve(r)-solve(l-1));
36     }
37 }
38 int main(){
39     acheing::main();
40     return 0;
41 }

bzoj上32ms。。

假装很快。。