2019 Multi-University Training Contest 5

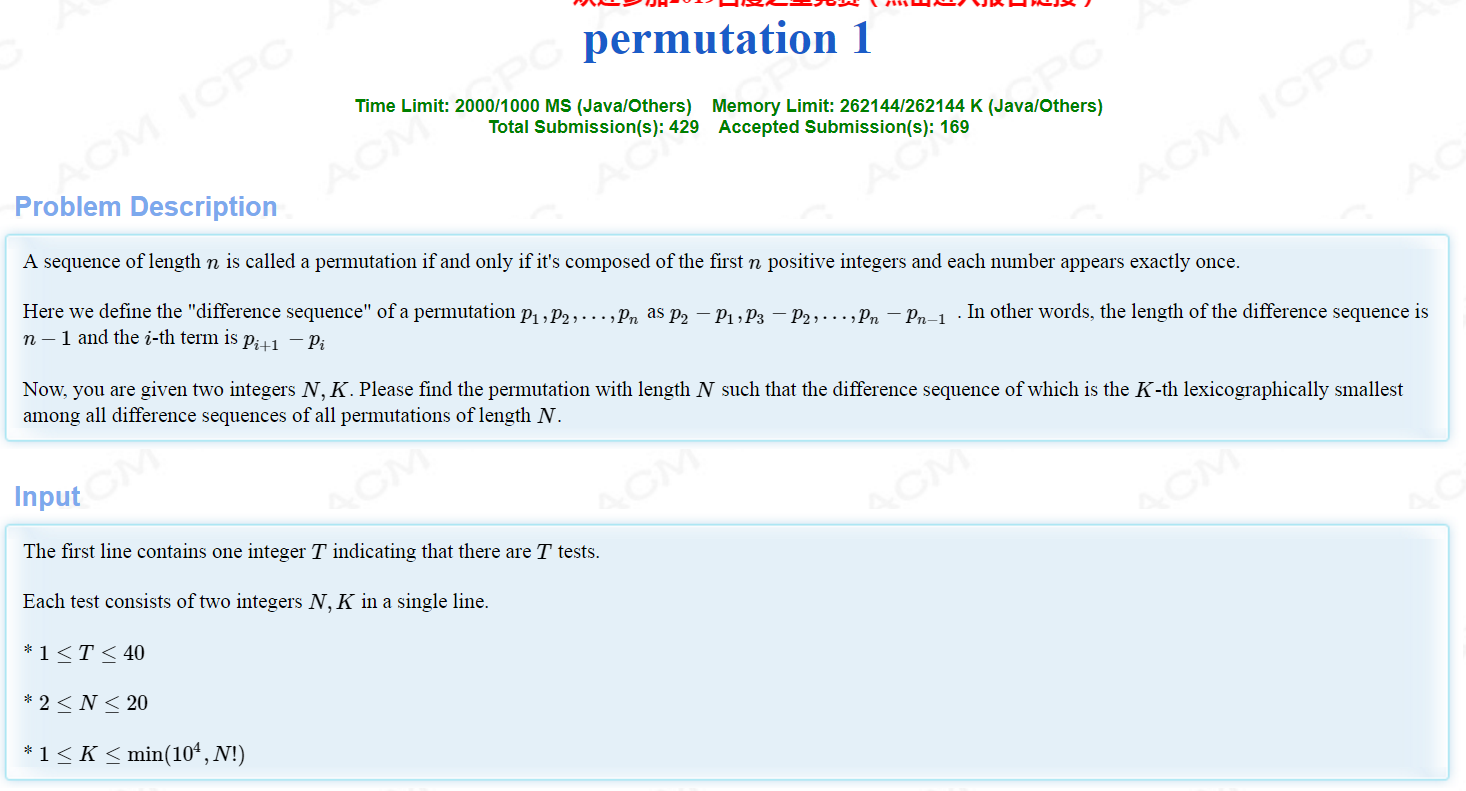
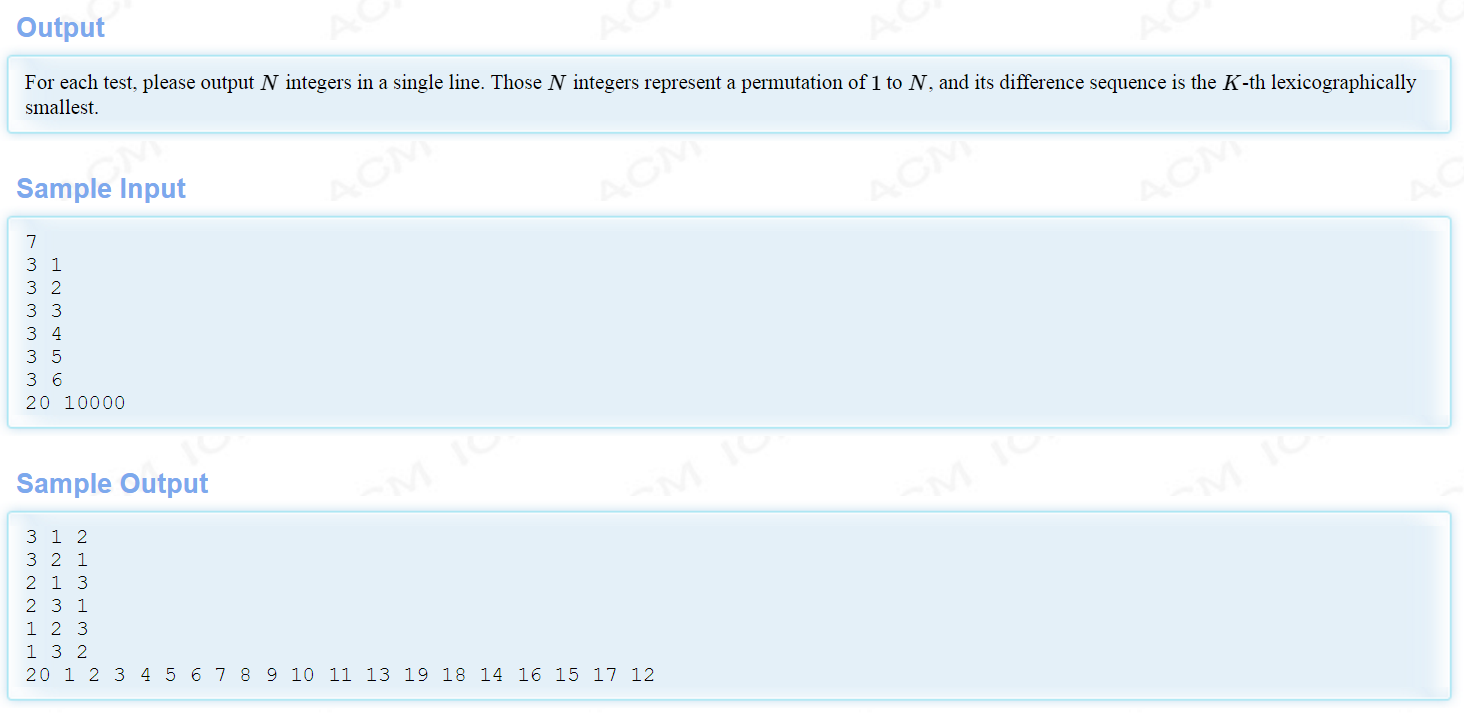
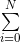permutation 2

Problem Description

You are given three positive integers N,x,y.
Please calculate how many permutations of 1∼N satisfies the following conditions (We denote the i-th number of a permutation by pi):

1. p1=x

2. pN=y

3. for all 1≤i<N, |pi−pi+1|≤2

Input

The first line contains one integer T denoting the number of tests.

For each test, there is one line containing three integers N,x,y.

* 1≤T≤5000

* 2≤N≤105

* 1≤x<y≤N

Output

For each test, output one integer in a single line indicating the answer modulo 998244353.

Sample Input

3
4 1 4
4 2 4
100000 514 51144

Sample Output

2
1
253604680

找规律

#include <bits/stdc++.h>
 
using namespace std;
typedef long long ll;
ll f[100210],n,x,y;
const ll mod=998244353;
int main()
{
    f[1]=1;
    f[2]=1;
    f[3]=1;
    f[4]=2;
    f[5]=3;
    for (ll i=6; i<=100020; i++)
    {
        f[i]=(f[i-2]+f[i-3]+f[i-4])%mod;
    }
    int T;
    scanf("%d",&T);
    while (T--)
    {
        scanf("%lld%lld%lld",&n,&x,&y);
        if (x==1&&y==2)
        {
            printf("1
");
            continue;
        }
        if (x==n-1&&y==n)
        {
            printf("1
");
            continue;
        }
        if (y-x==1)
        {
            printf("0
");
            continue;
        }
        if (y==n)
        {
               if (x==1) printf("%lld
",f[y-x+1]); else printf("%lld
",f[y-x]);
        }
        else
        {
            if (x==1)
            {
                printf("%lld
",f[y-x]);
            }
            else
            {
                printf("%lld
",f[y-x-1]);
            }
        }
    }
}

permutation 1

Problem Description

A sequence of length n is called a permutation if and only if it's composed of the first n positive integers and each number appears exactly once.

Here we define the "difference sequence" of a permutation p1,p2,…,pn as p2−p1,p3−p2,…,pn−pn−1. In other words, the length of the difference sequence is n−1 and the i-th term is pi+1−pi

Now, you are given two integers N,K. Please find the permutation with length N such that the difference sequence of which is the K-th lexicographically smallest among all difference sequences of all permutations of length N.

Input

The first line contains one integer T indicating that there are T tests.

Each test consists of two integers N,K in a single line.

* 1≤T≤40

* 2≤N≤20

* 1≤K≤min(104,N!)

Output

For each test, please output N integers in a single line. Those N integers represent a permutation of 1 to N, and its difference sequence is the K-th lexicographically smallest.

Sample Input

7
3 1
3 2
3 3
3 4
3 5
3 6
20 10000

Sample Output

3 1 2
3 2 1
2 1 3
2 3 1
1 2 3
1 3 2
20 1 2 3 4 5 6 7 8 9 10 11 13 19 18 14 16 15 17 12

equation

Problem Description

You are given two integers N,C and two integer sequences a and b of length N. The sequences are indexed from 1 to N.

Please solve the following equation for x:

 

, where |v| means the absolute value of v.

Input

The first line contains an integer T indicating there are T tests. Each test consists of N+1 lines. The first line contains two integers N,C. The i-th line of following Nlines consists of two integers ai,bi. 

* 1≤T≤50

* 1≤N≤105

* 1≤ai≤1000

* −1000≤bi≤1000

* 1≤C≤109

* only 5 tests with N larger than 1000

Output

For each test, output one line.
If there are an infinite number of solutions, this line consists only one integer −1.
Otherwise, this line first comes with an integer m indicating the number of solutions, then you must print m fractions from the smallest to the largest indicating all possible answers. (It can be proved that all solutions can be written as fractions). The fraction should be in the form of "a/b" where a must be an integer, b must be a positive integer, and gcd(abs(a),b)=1. If the answer is 0, you should output "0/1".

Sample Input

4
2 3
1 2
1 -1
3 3
2 1
2 2
2 3
2 1
3 5
4 -1
3 2
1 -1
1 -2
1 -3

 Sample Output

-1
2 -3/2 -1/2
0
1 2/1

n个绝对值方程把数轴分成n+1个部分，从左到右每个方程都变一次号

#include <bits/stdc++.h>
 
using namespace std;
const int maxn=200100;
typedef long long ll;
ll a,b,n,c,ka,kb,k,ff,dd;
set<pair<ll,ll> >s;
struct node
{
    ll a,b;
} d[maxn],ans[maxn];
 
bool cmp(node a,node b)
{
    return a.b*b.a<b.b*a.a;
}
 
int main() {
    int T;
    scanf("%d", &T);
    while (T--) {
        s.clear();
        memset(d,0, sizeof(d));
        k = ff = ka = kb = 0;
        scanf("%lld%lld", &n, &c);
        for (int i = 1; i <= n; i++) {
            scanf("%lld%lld", &d[i].a, &d[i].b);
            ka -= d[i].a;
            kb -= d[i].b;
            d[i].b = d[i].b * (-1);
        }
        sort(d + 1, d + n + 1, cmp);
        for (int i = 0; i <= n; i++) {
            ka += 2 * d[i].a;
            kb += 2 * (-1) * d[i].b;
            if (ka == 0 && kb == c) {
                ff = 1;
                break;
            }
            b = c - kb;
            a = ka;
            if (a < 0) {
                a *= -1;
                b *= -1;
            }
            dd = __gcd(a, abs(b));
            if (b * d[i + 1].a <= d[i + 1].b * a && d[i].a * b >= d[i].b * a) {
                k++;
                ans[k].a = a / dd;
                ans[k].b = b / dd;
            }
        }
        if (ff) {
            printf("-1
");
            continue;
        }
        for (int i = 1; i <= k; i++) {
            s.insert(make_pair(ans[i].a, ans[i].b));
        }
        k = 0;
        int len = s.size();
        if (len == 0) {
            printf("%d
", len);
            continue;
        }
        printf("%d", len);
        for (set<pair<ll, ll> >::iterator it = s.begin(); it != s.end(); it++) {
            k++;
            ans[k].a = it->first;
            ans[k].b = it->second;
        }
        sort(ans + 1, ans + k + 1, cmp);
        for (int i = 1; i <= k; i++) {
            printf(" %lld/%lld", ans[i].b, ans[i].a);
        }
        printf("
");
    }
}

string matching

Problem Description

String matching is a common type of problem in computer science. One string matching problem is as following:

Given a string s[0…len−1], please calculate the length of the longest common prefix of s[i…len−1] and s[0…len−1] for each i>0.

I believe everyone can do it by brute force.
The pseudo code of the brute force approach is as the following:

 We are wondering, for any given string, what is the number of compare operations invoked if we use the above algorithm. Please tell us the answer before we attempt to run this algorithm.

Input

The first line contains an integer T, denoting the number of test cases.
Each test case contains one string in a line consisting of printable ASCII characters except space.

* 1≤T≤30

* string length ≤106 for every string

Output

For each test, print an integer in one line indicating the number of compare operations invoked if we run the algorithm in the statement against the input string.

Sample Input

3
_Happy_New_Year_
ywwyww
zjczzzjczjczzzjc

Sample Output

17
7
32

#include <bits/stdc++.h>
 
using namespace std;
 
const int maxn=1001000;
typedef long long ll;
ll ans,next1[maxn],len;
char s[maxn];
 
void pre_ekmp(char x[],ll m,ll next[]) {
    next[0] = m;
    ll j = 0;
    while (j + 1 < m && x[j] == x[j + 1]) {
        j++;
    }
    next[1] = j;
    ll k = 1;
    for (ll i = 2; i < m; i++) {
        ll p = next[k] + k - 1;
        ll L = next[i - k];
        if (i + L < p + 1) {
            next[i] = L;
        } else {
            j = max(0ll, p - i + 1);
            while (i + j < m && x[i + j] == x[j]) {
                j++;
            }
            next[i] = j;
            k = i;
        }
    }
}
 
int main(){
    int T;
    scanf("%d",&T);
    while (T--){
        ans=0;
        scanf("%s",s);
        len=strlen(s);
        pre_ekmp(s,len,next1);
        for (ll i=1;i<len;i++){
            if (i+next1[i]<len) ans+=next1[i]+1;else ans+=next1[i];
        }
        printf("%lld
",ans);
    }
}

permutation 1

 

#include<bits/stdc++.h>

using namespace std;

struct node{
    int tmp[30];
}a[100010];
int n,k,ans[30];
bool cmp1(node a,node b){
    for (int i=1;i<n;i++){
        if (a.tmp[i+1]-a.tmp[i]==b.tmp[i+1]-b.tmp[i]){
            continue;
        }
        return a.tmp[i+1]-a.tmp[i]<b.tmp[i+1]-b.tmp[i];
    }
}

bool cmp2(node a,node b){
    a.tmp[0]=n-8;
    b.tmp[0]=n-8;
    for (int i=0;i<8;i++){
        if (a.tmp[i+1]-a.tmp[i]==b.tmp[i+1]-b.tmp[i]){
            continue;
        }
        return a.tmp[i+1]-a.tmp[i]<b.tmp[i+1]-b.tmp[i];
    }
}

int tmpans[9],tot;
int vis[30];

void dfs1(int x){
    if (x==n+1){
        tot++;
        for (int i=1;i<=n;i++){
            a[tot].tmp[i]=ans[i];
        }
        return;
    }
    for (int i=1;i<=n;i++){
        if (!vis[i]){
            ans[x]=i;
            vis[i]=1;
            dfs1(x+1);
            vis[i]=0;
        }
    }
}

void dfs2(int x){
    if (x==9){
        tot++;
        for (int i=1;i<=8;i++){
            a[tot].tmp[i]=ans[i];
        }
        return;
    }
    for (int i=n-8;i<=n-1;i++){
        if (!vis[i]){
            ans[x]=i;
            vis[i]=1;
            dfs2(x+1);
            vis[i]=0;
        }
    }
}

int main(){
    int T;
    scanf("%d",&T);
    while (T--){
        scanf("%d%d",&n,&k);
        memset(vis,0,sizeof(vis));
        if (n>8){
            tot=0;
            printf("%d ",n);
            for (int i=1;i<n-8;i++){
                printf("%d ",i);
            }
            dfs2(1);
            sort(a+1,a+tot+1,cmp2);
            for (int i=1;i<8;i++){
                printf("%d ",a[k].tmp[i]);
            }
            printf("%d
",a[k].tmp[8]);
        }else{
            tot=0;
            dfs1(1);
            sort(a+1,a+tot+1,cmp1);
            for (int i=1;i<n;i++){
                printf("%d ",a[k].tmp[i]);
            }
            printf("%d
",a[k].tmp[n]);
        }
    }
}

fraction

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll p,x,y,a;
void ggcd(ll pa,ll pb,ll qa,ll qb,ll &x,ll &y){
    ll z=(pa+pb)/pb;
    if (z<=qa/qb){
        x=z;
        y=1;
        return;
    }
    pa-=(z-1)*pb;
    qa-=(z-1)*qb;
    ggcd(qb,qa,pb,pa,y,x);
    x+=(z-1)*y;
}
int main(){
    int T;
    scanf("%d",&T);
    while (T--){
        scanf("%lld%lld",&p,&a);
        ggcd(p,a,p,a-1,x,y);
        printf("%lld/%lld
",x*a-p*y,x);
    }
}

three arrays

discrete logarithm problem

line symmetric

find hidden array