题目大意:N头牛,F个食物,D个饮料。每一个食物和饮料只能分享给一头牛,每一头牛也最多获得一个饮料和一个食物,问最多有几头牛可以同时获得一个食物和一个饮料?
这是一个典型的最大流问题。难点在于建图,建完图就是最大流裸题了。
关于见图。
每头牛都有喜欢的食物和饮料,首先看对牛与食物和牛与饮料分别被建边。注意到饮料和食物是毫无关系的。食物是食物,饮料是饮料,并不能相互代替。因此我们见图的时候可以用食物指向牛,牛指向饮料(反过来也可以)。注意,每头牛最多获得一个食物和饮料,这时候就需要对顶点进行限流。即牛与牛之间要加一条边权为1的边。
最终建成的图应该是这样的:
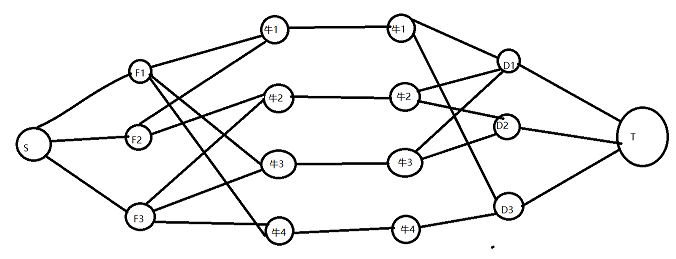
边均为有向边,方向均指向右方。
code:
#include<iostream> #include<cstdio> #include<cstring> #include<queue> using namespace std; const int INF=1e9+7; const int N=1E4+7; struct stu{ int to,val,nxt; }edge[N]; int n,f,d; int dis[N]; int head[N],tol=0; void add(int x,int y,int z){ edge[tol].to=y; edge[tol].val=z; edge[tol].nxt=head[x]; head[x]=tol++; } bool bfs(int s,int t){ for(int i=0;i<=n+n+f+d+1;i++) dis[i]=INF; queue<int>que; dis[s]=0; que.push(s); while(!que.empty()){ int u=que.front(); que.pop(); for(int i=head[u];i!=-1;i=edge[i].nxt){ int v=edge[i].to; int w=edge[i].val; if(w>0&&dis[u]+1<dis[v]) { dis[v]=dis[u]+1; que.push(v); } } } return dis[t]!=INF; } int dfs(int s,int t,int mn){ if(s==t) return mn; for(int i=head[s];i!=-1;i=edge[i].nxt){ int v=edge[i].to; int w=edge[i].val; if(w<=0||dis[v]!=dis[s]+1) continue ; int cw=dfs(v,t,min(w,mn)); if(cw>0){ edge[i].val-=cw; edge[i^1].val+=cw; return cw; } } return 0; } void dicnic(int s,int t){ int ans=0; while(bfs(s,t)){ int d; while((d=dfs(s,t,INF))!=0){ ans+=d; } } cout<<ans<<endl; } int main(){ memset(head,-1,sizeof head); cin>>n>>f>>d; int s=0,t=n+n+f+d+1;//源点与汇点 for(int i=1;i<=n;i++){//牛。 int t1,t2,food,drink; cin>>t1>>t2; for(int j=1;j<=t1;j++){ cin>>food; add(food+n+n,i,1); add(i,food+n+n,0); } for(int j=1;j<=t2;j++){ cin>>drink; add(i+n,drink+n+n+f,1); add(drink+n+n+f,i+n,0); } } for(int i=1;i<=n;i++){ add(i,i+n,1); add(i+n,i,0); } for(int i=1;i<=f;i++){ add(s,n+n+i,1); add(n+n+i,s,0); } for(int i=1;i<=d;i++){ add(n+n+f+i,t,1); add(t,n+n+f+i,0); } dicnic(s,t); return 0; }